线性回归算法学习总结(一)
作用
预测趋势,从样本数据中找到一个数学模型,找到事物的客观存在的规律。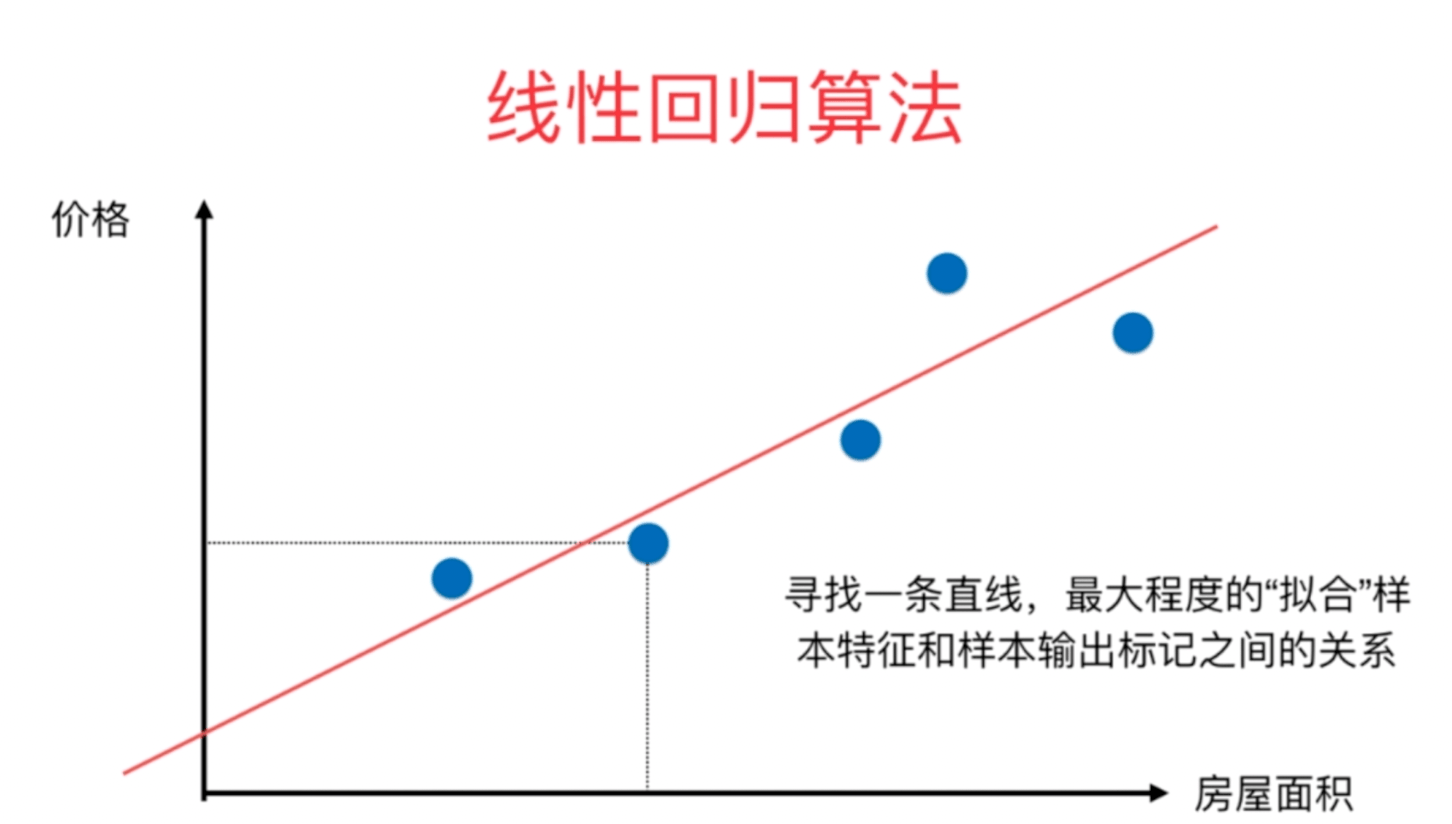
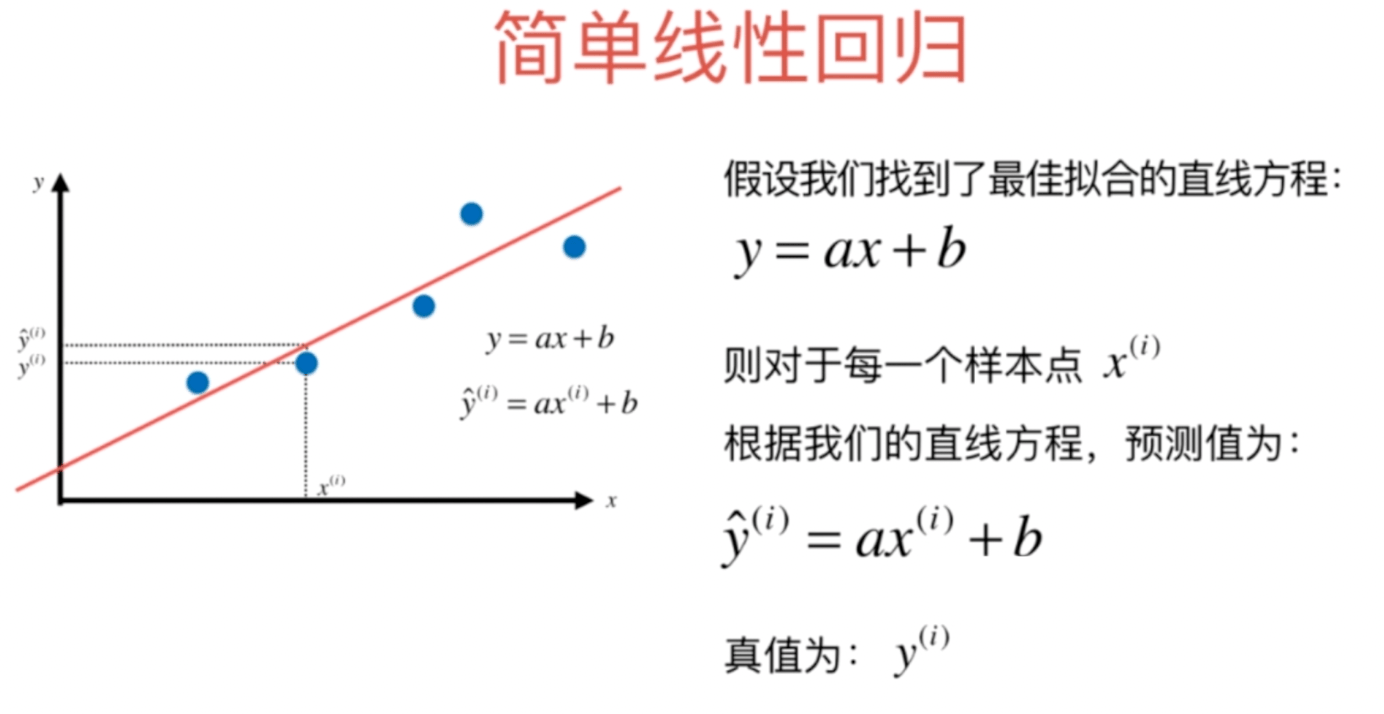
我们希望y ^ { ( i ) }和\hat { y } ^ { ( i ) }的差距尽量小。
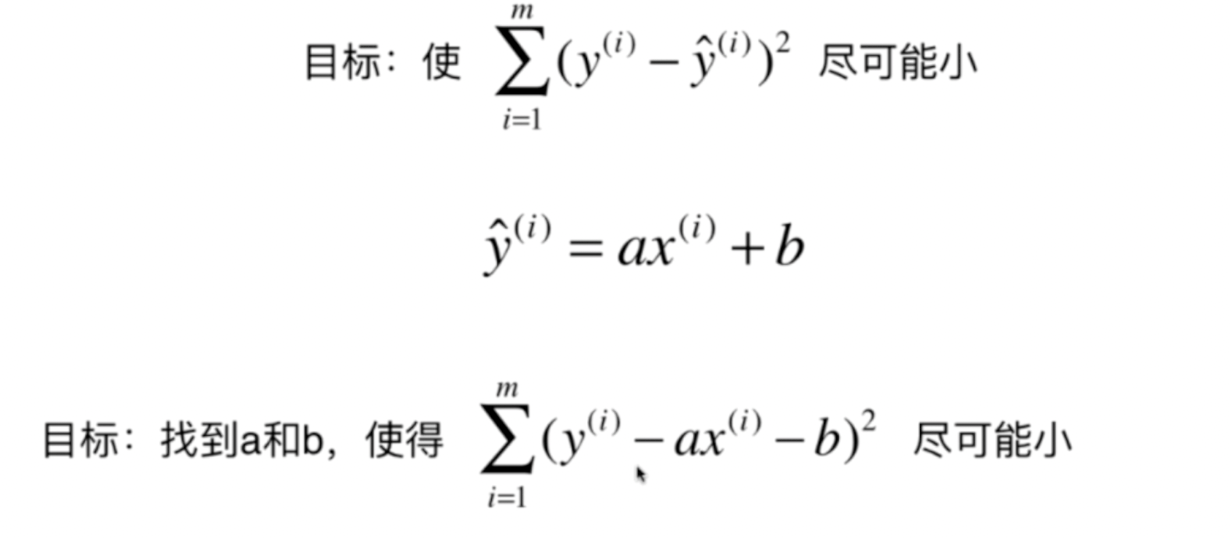
导数为0取得极值:

最终求得如下结果:

简单线性回归的实现
封装通用方法
import numpy as np
class SimpleLinearRegression1:
def __init__(self):
self.a_ = None
self.b_ = None
def fit(self, x_train, y_train):
"""根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
num = 0.0
d = 0.0
#zip() 将可迭代的对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。
for x, y in zip(x_train, y_train):
num += (x - x_mean) * (y - y_mean)
d += (x - x_mean) ** 2
self.a_ = num / d
self.b_ = y_mean - self.a_ * x_mean
return self
def predict(self, x_predict):
"""给定待预测数据集x_predict,返回表示x_predict的结果向量"""
assert x_predict.ndim == 1, \
"Simple Linear Regressor can only solve single feature training data."
assert self.a_ is not None and self.b_ is not None, \
"must fit before predict!"
return np.array([self._predict(x) for x in x_predict])
def _predict(self, x_single):
"""给定单个待预测数据x,返回x的预测结果值"""
return self.a_ * x_single + self.b_
def __repr__(self):
return "SimpleLinearRegression1()"
使用
import numpy as np
import matplotlib.pyplot as plt
from playML.SimpleLinearRegression import SimpleLinearRegression1
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])
reg1 = SimpleLinearRegression1()
reg1.fit(x, y)
reg1.predict(np.array([x_predict]))最小二乘法(多元线性回归)
主要思想就是求解未知参数,使得理论值与观测值之差(即误差)的平方和达到最小。
所谓最小二乘,也可以叫做最小平方和,其目的就是通过最小化误差的平方和,使得拟合对象无限接近目标对象,最小二乘法可以用于对函数的拟合。
观测值就是我们的多组样本,理论值就是我们的假设拟合函数。举一个最简单的线性回归的简单例子,比如我们有m个只有一个特征的样本:( x _ { i } , y _ { i } ) ( i = 1 , 2 , 3 ,\cdots,m) ,样本采用一般的y ( x )为n次的多项式拟合:
y=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{n} x_{n}
其中 \hat{y}^{(i)}为预测值,\hat{y}^{(i)}=\theta_{0}+\theta_{1} X_{1}^{(i)}+\theta_{2} X_{2}^{(i)}+\ldots+\theta_{n} X_{n}^{(i)}
最小二乘法就是要找到一组向量\theta ( \theta _ { 0 } , \theta _ { 1 } , \theta _ { 2 } , \cdots , \theta _ { n } )使得 \sum_{i=1}^{m}\left(y^{(i)}-\hat{y}^{(i)}\right)^{2}最小
令
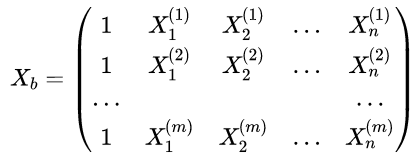
预测值:\hat{y}^{(i)} = X _ { b } \cdot \theta
多元线性回归的正规方程解(Normal Equation): \theta = \left( X _ { b } ^ { T } X _ { b } \right) ^ { - 1 } X _ b ^ { T } y
时间复杂度高:O(n^3)

最小二乘法的局限性
- 如果拟合函数不是线性的,这时无法使用最小二乘法。
- 特征 n 非常的大的时候不可行,建议超过10000个特征就用迭代法
向量化
对应a可以看为2个向量的运算:
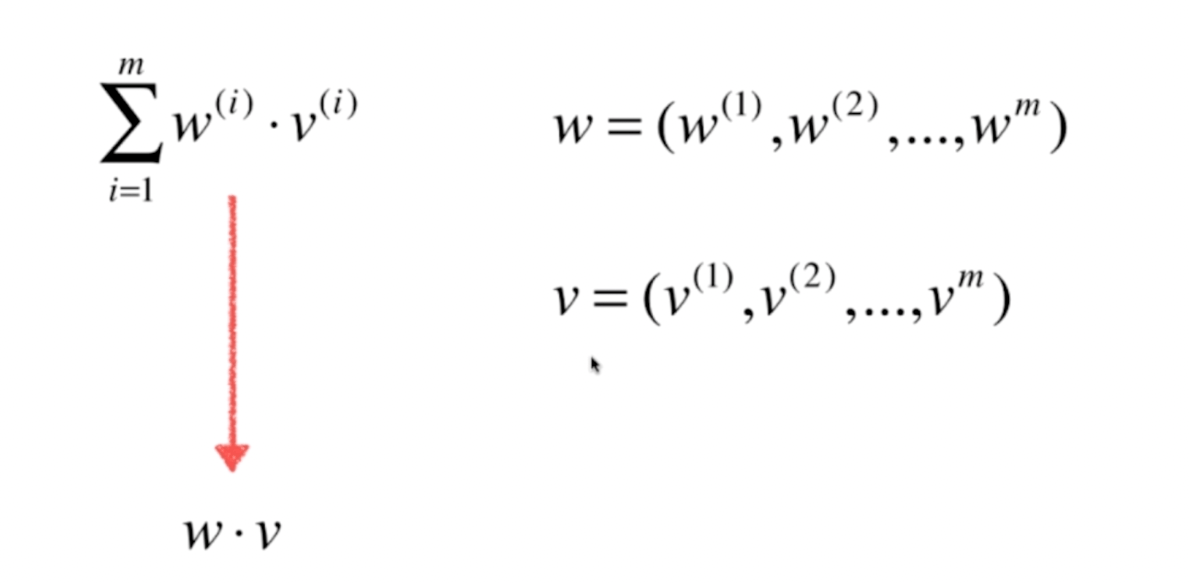
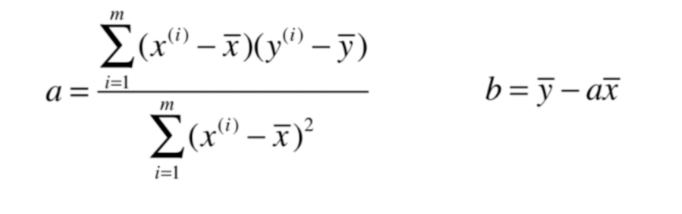
修改为向量化代码如下:
def fit(self, x_train, y_train):
"""根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)
self.b_ = y_mean - self.a_ * x_mean
return self回归算法的评价
均方误差MSE

def mean_squared_error(y_true, y_predict):
return np.sum((y_true - y_predict)**2) / len(y_true)均方根误差RMSE (Root Mean Squared Error)

def root_mean_squared_error(y_true, y_predict):
"""计算y_true和y_predict之间的RMSE"""
return sqrt(mean_squared_error(y_true, y_predict))平均绝对误差MAE(Mean Absolute Error)

def mean_absolute_error(y_true, y_predict):
"""计算y_true和y_predict之间的MAE"""
return np.sum(np.absolute(y_true - y_predict)) / len(y_true)R Square

R^2 <=1
R^2越大越好。当我们的预测模型不犯任何错误是,$R^2$ 得到最大值1
当我们的模型等于基准模型时,$R^2$为0
如果R^2<0,说明我们学习到的模型还不如基准模型。此时,很有可能我们的数据不存在任何线性关系。
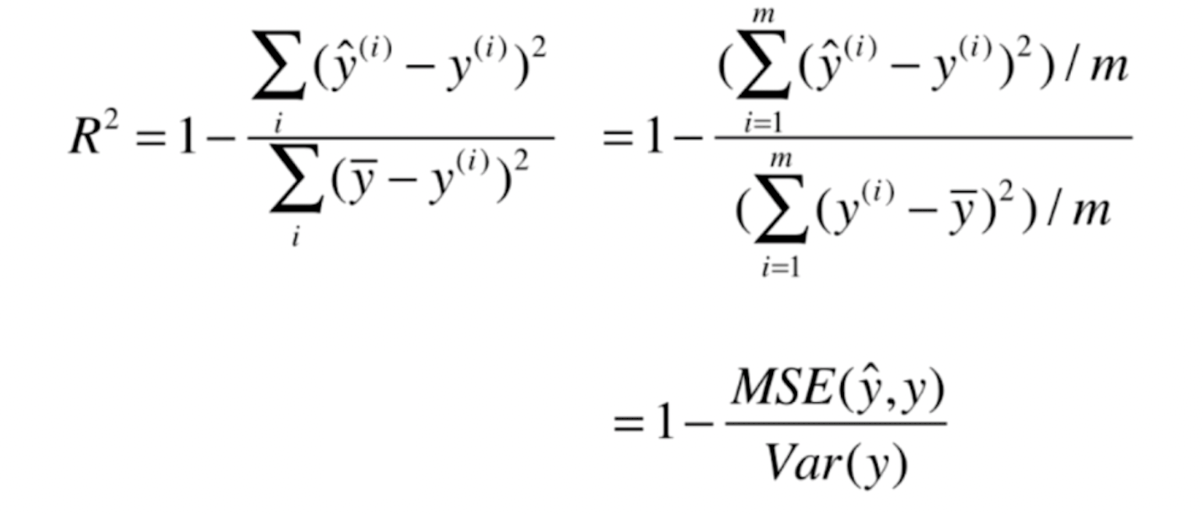
def r2_score(y_true, y_predict):
"""计算y_true和y_predict之间的R Square"""
return 1 - mean_squared_error(y_true, y_predict)/np.var(y_true)本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu




推荐文章: