直方图中最大矩形

题面

给出n个数字，代表直方图的条高，直方图每一条的宽度为1，请计算直方图中最大矩形的面积

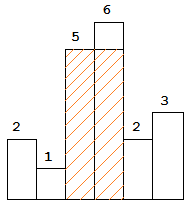
上图是每条宽度为1, 高度 =[2,1,5,6,2,3].的直方图
图中的阴影部分是该直方图中面积最大的矩形，面积为10个单位
输入

[2,1,5,6,2,3]

返回

10

暴力双指针

1. 双指针滑动窗口确定矩形长
2. 以当前高程为基准左右边界水平扩展
3. 遍历小于基准停止扩展，计算矩形图面积，留大值

   func largestRectangleArea( height []int ) int {
       var max int
       for i:=0;i<len(height);i++{
           if height[i] !=0 {
               left,right := i,i
               for right < len(height)-1 && height[right+1] >= height[i]{
                   right++
               }
               for left > 0 && height[left-1] >= height[i] {
                   left--
               }
               if cur := height[i] *(right - left + 1);cur > max {
                   max = cur
               }
           }
       }
       return max
   }

单调栈

• 较小的元素会成为矩形高的限制条件
• 构建单调栈，所有的单调递增留至最后计算
• 在数组最后添加了一个0，保证遍历最后一个元素时栈被清空，及计算的越界需求
• 栈底元素出栈后，当前索引长视为矩形长

  func largestRectangleArea( height []int ) int {
        var max int
        height = append(height, 0)  //简化代码，确保栈被清空
        for st,i:=[]int{},0;i<len(height);i++{
            for len(st)>0 && height[st[len(st)-1]] > height[i]{
                h:=height[st[len(st)-1]]
                st = st[:len(st)-1]
                leftIdx:=-1
                if len(st)>0{
                    leftIdx = st[len(st)-1]
                }
                if cur := h*(i- leftIdx -1); cur > max {
                    max = cur
                }
            }
            st = append(st, i)
        }
        return max
  }

本作品采用《CC 协议》，转载必须注明作者和本文链接