反导数

微分记号

有一个函数y=f(x)，y的微分记作\mathrm{d}y，它的定义是：

\displaystyle \mathrm{d}y=f^\prime(x)\mathrm{d}x

这就是微分的记法。又因为y等于f，有时候我们又称它为f的微分。

\displaystyle \Leftrightarrow\frac{\mathrm{d}y}{\mathrm{d}x}=f^\prime(x)

这是莱布尼茨对于导数的记法，也就是把导数记为两个无穷小量的比。
莱布尼茨记法的思想是用\mathrm{d}x代替\Delta x，\mathrm{d}y代替\Delta y。这是一种动态记法。

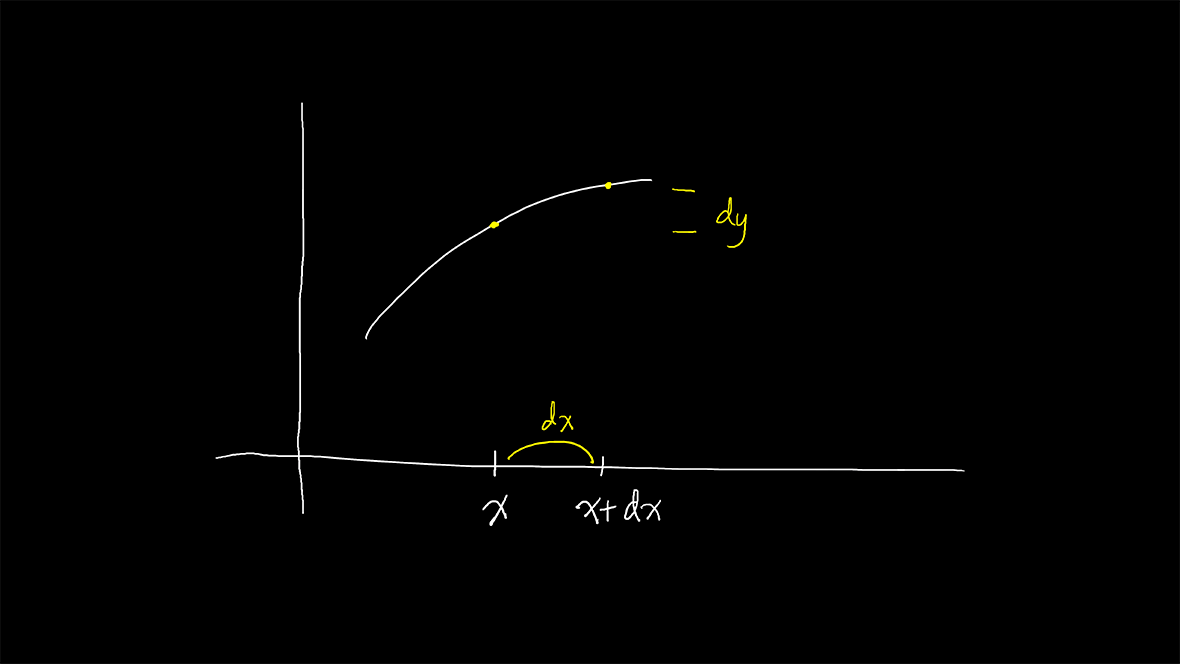
反导数

我们来看一下g(x)dx的积分记作：

\displaystyle \int g(x)dx

G(x)是g(x)dx的积分：

\displaystyle G(x)=\int g(x)dx

我们用g(x)创造了一个新函数G(x)，这个新函数就叫做g的「反导数」。
\int是积分符号，整个式子称作「不定积分」。g的反导数又叫作g的不定积分。

细心点的朋友会发现前面章节写的dx是\mathrm{d}x，有意的把\mathrm{d}的字体区分开来，为的是不让新手把\mathrm{d}当作一个变量，它只是需要和变量写在一起成为微分符号才有作用。后面我将不会区分\mathrm{d}的字体，将\mathrm{d}x直接写作dx。

小试牛刀一下：

\displaystyle \int \sin xdx=-\cos x\\{}\\ G(x)=-\cos x\\{}\\ G^\prime(x)=\sin x

实际上这真的就一定正确吗？我们来纠正下上式的错误：

\displaystyle \int \sin xdx=-\cos x+c\\{}\\ G(x)=-\cos x+c\\{}\\ G^\prime(x)=\sin x

我们看到后面有跟了「常数c」,因为在求导过程中常数消掉了，那么求反导中，也要注意这一细节，尽管c可能原来就是0，但这也算是常数，因为我们不能确定它一定是0。
再举个例子：

\displaystyle \int (\cos x+c)dx=\sin x+c_1x+c_2

后面的c_1代表\cos x+c的c。
这些常数导致了这些积分是不定的，所以称为「不定积分」。

\displaystyle \int x^adx=\frac{1}{a+1}x^{a+1}+c\\{}\\ a\not=-1\\{}\\ d(x^{a+1})=(a+1)x^adx\\{}\\ \forall a

来看看\ln：

\displaystyle \int \frac{dx}{x}=\ln|x|+c

上式如果x>0OK，如果x< 0：

\displaystyle \frac{d}{dx}\ln|x|=\frac{d}{dx}\ln(-x)\\{}\\ =\frac{1}{-x}\frac{d}{dx}(-x)=\frac{-1}{-x}=\frac{1}{x}

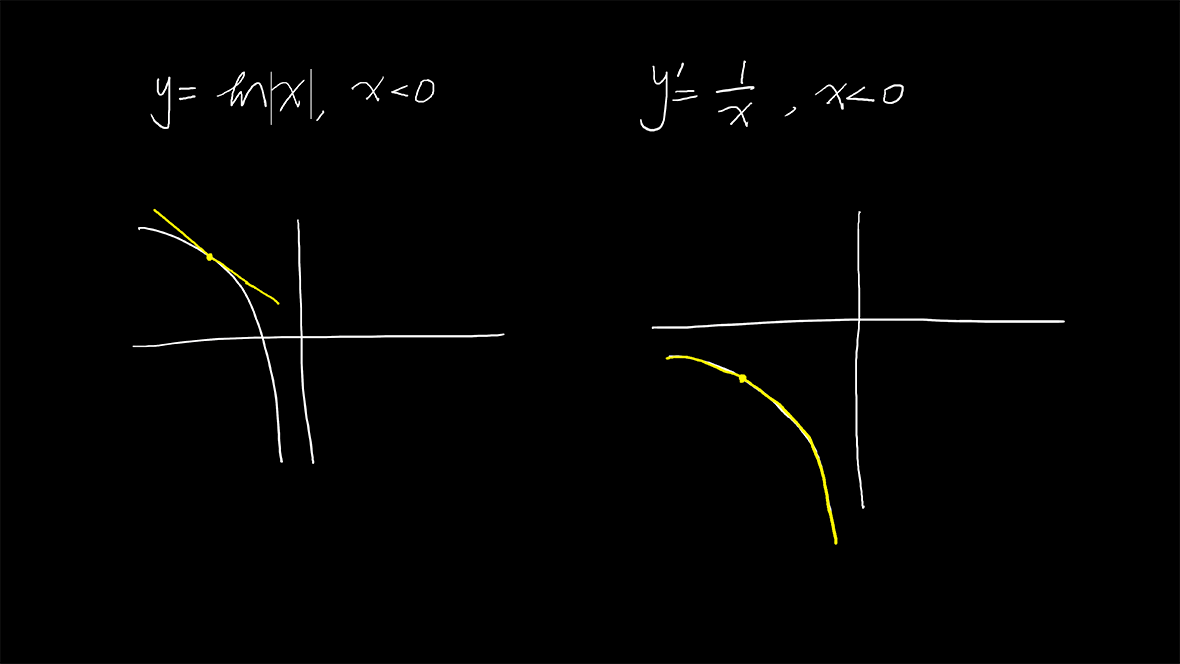
通常我们不写绝对值符号，只考虑x>0的情况。

再来点不定积分的例子：

\displaystyle \int \sec^2xdx=\tan x+c\\{}\\ \int\frac{dx}{\sqrt{1-x^2}}=\sin^{-1}x+c\\{}\\ \int\frac{dx}{1+x^2}=\tan^{-1}x+c