微积分第一基本定理

微积分第一基本定理

\displaystyle F^\prime(x)=f(x)\\{}\\ \int_a^bf(x)dx=F(b)-F(a)=F(x)\bigg|_a^b

来个例子：

\displaystyle F(x)=\frac{x^3}{3}\\{}\\ F^\prime(x)=x^2\\{}\\ \int_a^bx^2dx=F(b)-F(a)=\frac{b^3}{3}-\frac{a^3}{3}\\{}\\ a=0\\{}\\ \int_0^bx^2dx=\frac{x^3}{3}\bigg|_0^b=\frac{b^3}{3}-\frac{0^3}{3}=\frac{b^3}{3}

来计算下下图绿色阴影部分面积：

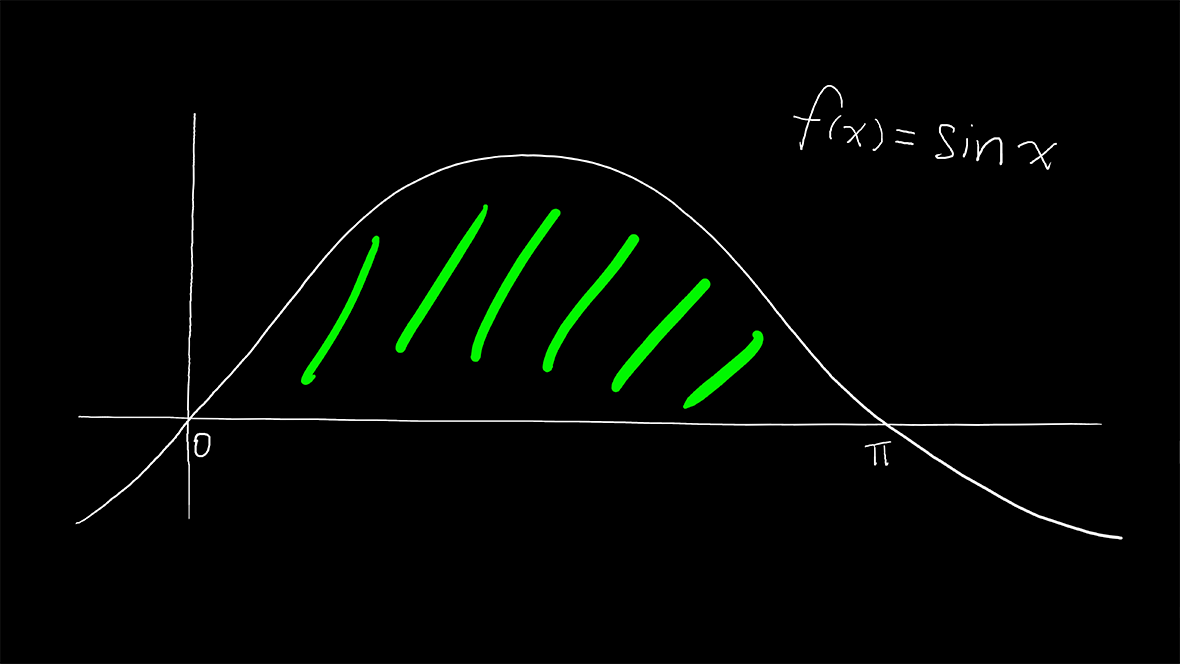```math \displaystyle \int_0^\pi\sin xdx=(-\cos x)\bigg|_0^\pi\\{}\\ =-\cos \pi-(-\cos0)\\{}\\ =-(-1)-(-1)=2 ``` 再来个例子： ```math \displaystyle \int_0^1x^{99}dx=\frac{x^{100}}{100}\bigg|_0^1=\frac{1}{100} ```

假设你驾驶一辆小车从a地点去b地点，\displaystyle f^\prime(t)=\frac{df}{dt}=v(t)，f(t)是距离，v(t)是速度，t是时间。
我们用黎曼和来表示下：

\displaystyle \sum_{i=1}^nv(t_i)\Delta t\xlongequal[连续化]{\thicksim}\int_a^bv(t)dt=f(b)-f(a)

其中\Delta x是1秒钟的刻度，v(t_i)是每秒的速度表读数，n代表总读秒数，这是一个很好的积分近似。右边的积分则是无限小的刻度dt。最后得出的是这段路程总共行驶的距离。

但实际上距离是可以为负的，比如：

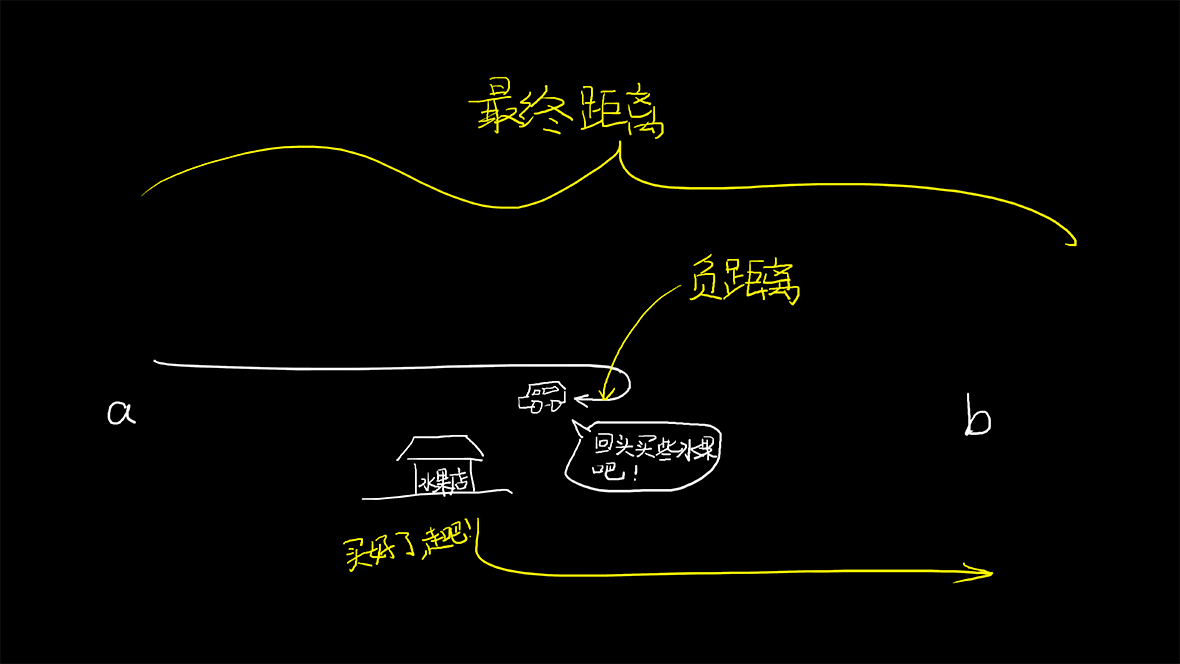
看下面的积分：

\displaystyle \int_0^{2\pi}\sin xdx=(-\cos x)\bigg|_0^{2\pi}\\{}\\ =-\cos 2\pi-(-\cos0)\\{}\\ =-1-(-1)=0

最后积出了0，看下图解：

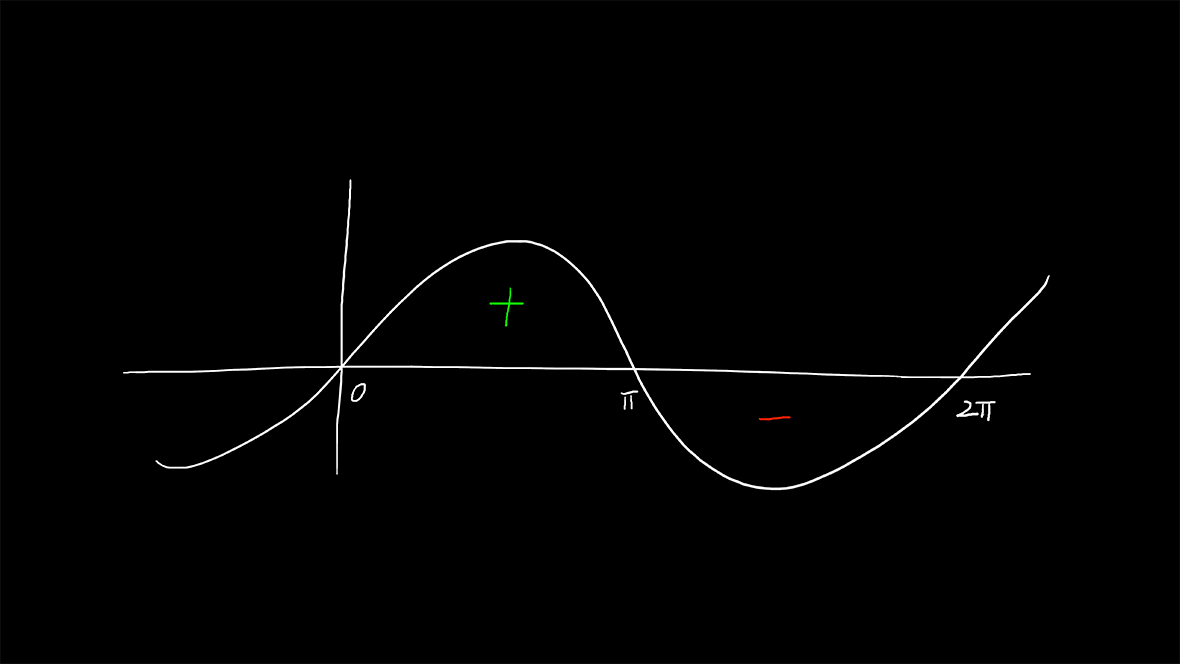#### 定积分的几何解释： 自变量轴上方的面积减去自变量轴下方的面积。 在上面的驾驶问题中的自变量轴是$$t$$轴。

所以我们的距离公式有两个：
只计算位移（走过的净距离）：

\displaystyle \int_a^bv(t)dt

计算总距离：

\displaystyle \int_a^b\big|v(t)\big|dt