微积分第二基本定理
微积分第二基本定理
这其实是微积分基本定理的另一种形式,我们接下来换个角度理解它。
\displaystyle F(b)-F(a)=\int_a^bf(x)dx\\{}\\ \Delta F=F(b)-F(a)\\{}\\ \Delta x=b-a\\{}\\ \Delta F=\int_a^bf(x)dx\\{}\\ \frac{\Delta F}{\Delta x}=\frac{1}{b-a}\int_a^bf(d)dx\\{}\\ =Average(f)\\{}\\ \Delta F=[Ave(F^\prime)]\Delta x
可以看到一个函数的增量,等于它导数区域的平均值乘以该函数自变量的增量。
\displaystyle a=0,b=n\\{}\\ \frac{f(1)+f(2)+...+f(n)}{n}\approx\frac{1}{n}\int_0^nf(x)dx\\{}\\ \Delta x=1
推广到中值定理:
\displaystyle (_{a< x< b}\min F)\Delta x\leqslant\Delta F=F^\prime(\xi)\Delta x\leqslant(_{a<\xi< b}\max F^\prime)\Delta x\\{}\\ (\min F)\Delta x\leqslant\Delta F=[Ave(F^\prime)]\Delta x\leqslant(\max F^\prime)\Delta x
例:
我们有函数
\displaystyle F^\prime(x)=\frac{1}{1+x},F(0)=1\\{}\\
问:MTV 暗示A< F(4)< B时,A、B是多少?
\displaystyle F(4)-F(0)=F^\prime(\xi)(4-0)=\frac{1}{1+\xi}\cdot4\\{}\\ \frac{1}{1+0}\cdot4\to\frac{1}{1+4}\cdot4\\{}\\ \frac{4}{5}< F(4)-F(0)< 4\\{}\\ \frac{9}{5}< F(4)< 5
微积分第一基本定理来解释:
\displaystyle F(4)-F(0)=\int_0^4\frac{dx}{1+x}\\{}\\ \int_0^4\frac{1}{5}dx=\frac{4}{5}<\int_0^4\frac{dx}{1+x}\\{}\\ <\int_0^4dx=4
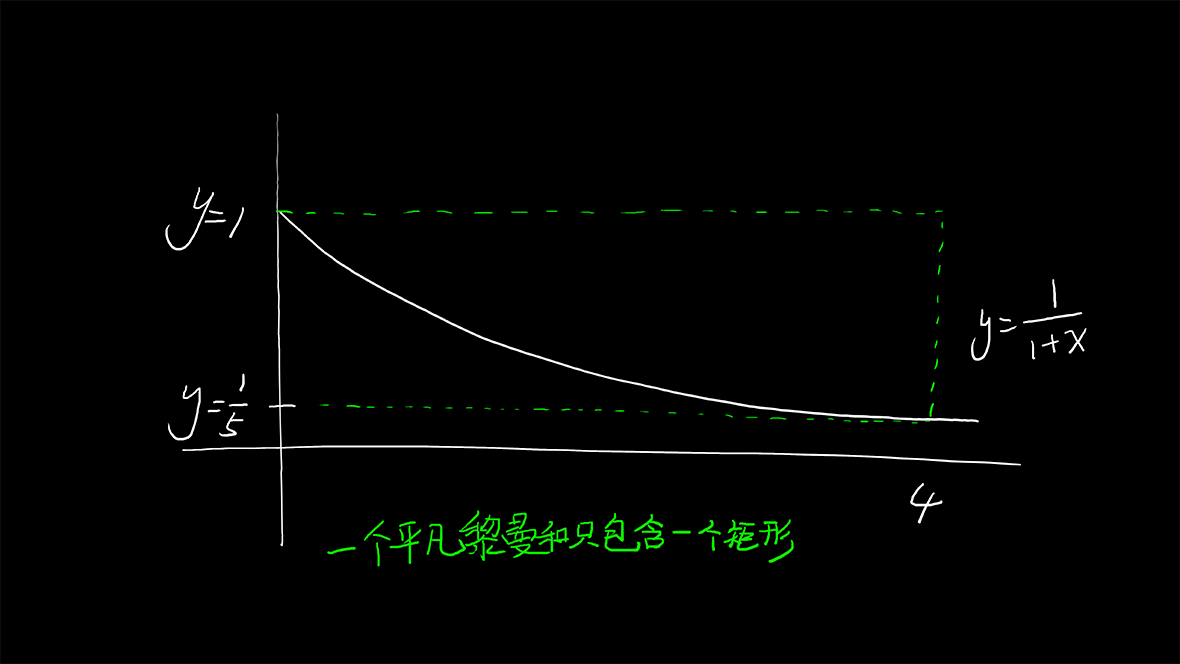
\displaystyle 下黎曼和<\int_0^4\frac{dx}{1+x}<上黎曼和
我们来看下微积分第二基本定理:
如果f是连续的,以及
\displaystyle G(x)=\int_a^xf(x)dx=\int_a^xf(t)dt\\{}\\ a\leqslant t_{_{哑变量}}\leqslant x
那么:
G^\prime(x)=f(x)
注意上面的积分上下限,在这里我这样用了,因为t是「哑变量」,但一般千万别这样用。
G(x)可以用来求解微分方程y^\prime=f(x)。
\displaystyle \left\{ \begin{aligned} & y^\prime=f\\ & y(a)=0 \end{aligned} \right.
这个方程给出了变化率和初始位置。
例 1:
\displaystyle \frac{d}{dx}\int_1^x\frac{dt}{t^2}=\frac{1}{x^2}\\{}\\ \begin{aligned} \int_1^x\frac{dt}{t^2}=G(x)&&G^\prime(x)=f(x) \end{aligned}\\{}\\ \begin{aligned} \int_1^xf(t)dt&&f(t)=\frac{1}{t^2} \end{aligned}
例 2:
\displaystyle \int_1^xt^{-2}dt=-t^{-1}\bigg|_1^x=-\frac{1}{x}-(-1)\\{}\\ \begin{aligned} \frac{d}{dx}(1-\frac{1}{x})=\frac{1}{x^2}&&G(x)=1-\frac{1}{x} \end{aligned}
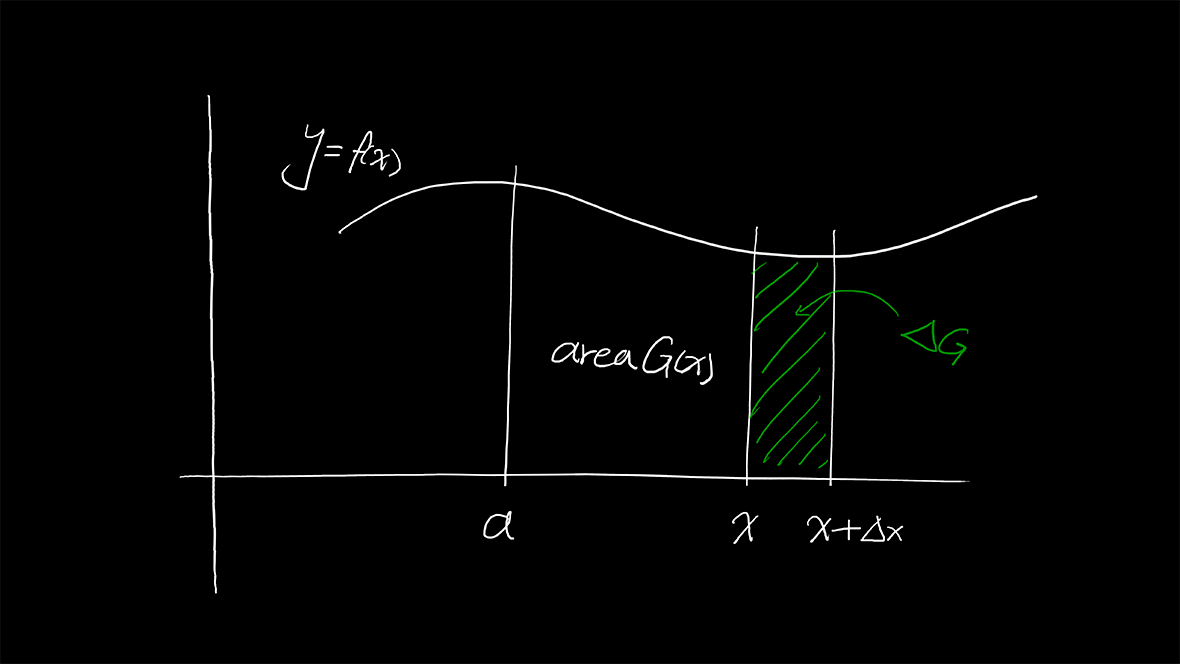
\displaystyle \Delta G\approx\Delta xf(x)\\{}\\ \lim_{\Delta x\to0}\frac{\Delta G}{\Delta x}=f(x)\\{}\\ G^\prime(x)=f(x)\\{}\\ f^\prime(x)=G^\prime(x)\\{}\\ \Rightarrow F(x)=G(x)+c\\{}\\ \because F^\prime=f\\{}\\ F(b)-F(a)=G(b)+c-(G(a)+c)\\{}\\ =G(b)-G(a)\\{}\\ G(a)=\int_a^a...=0\\{}\\ G(b)-G(a)=\int_a^bf(x)dx-0\\{}\\ G(x)=\int_a^xf(t)dt
例:
\displaystyle \begin{aligned} F(x)=\frac{-1}{x},&&F^\prime(x)=\frac{1}{x^2} \end{aligned}\\{}\\ G(x)=1-\frac{1}{x}\\{}\\ \int_1^2\frac{dt}{t^2}=\overbrace{\frac{-1}{t}\bigg|_1^2}^{F(x)}=\overbrace{(1-\frac{1}{t})\bigg|_1^2}^{G(x)}\\{}\\ \begin{aligned} L^\prime(x)=\frac{1}{x},&&L(1)=0 \end{aligned}\\{}\\ L(x)=\int_1^x\frac{dt}{t}

 单变量微积分入门
单变量微积分入门

 关于 LearnKu
关于 LearnKu



