[Leetcode 之 PHP 解析 (42. Trapping Rain Water)
题目介绍
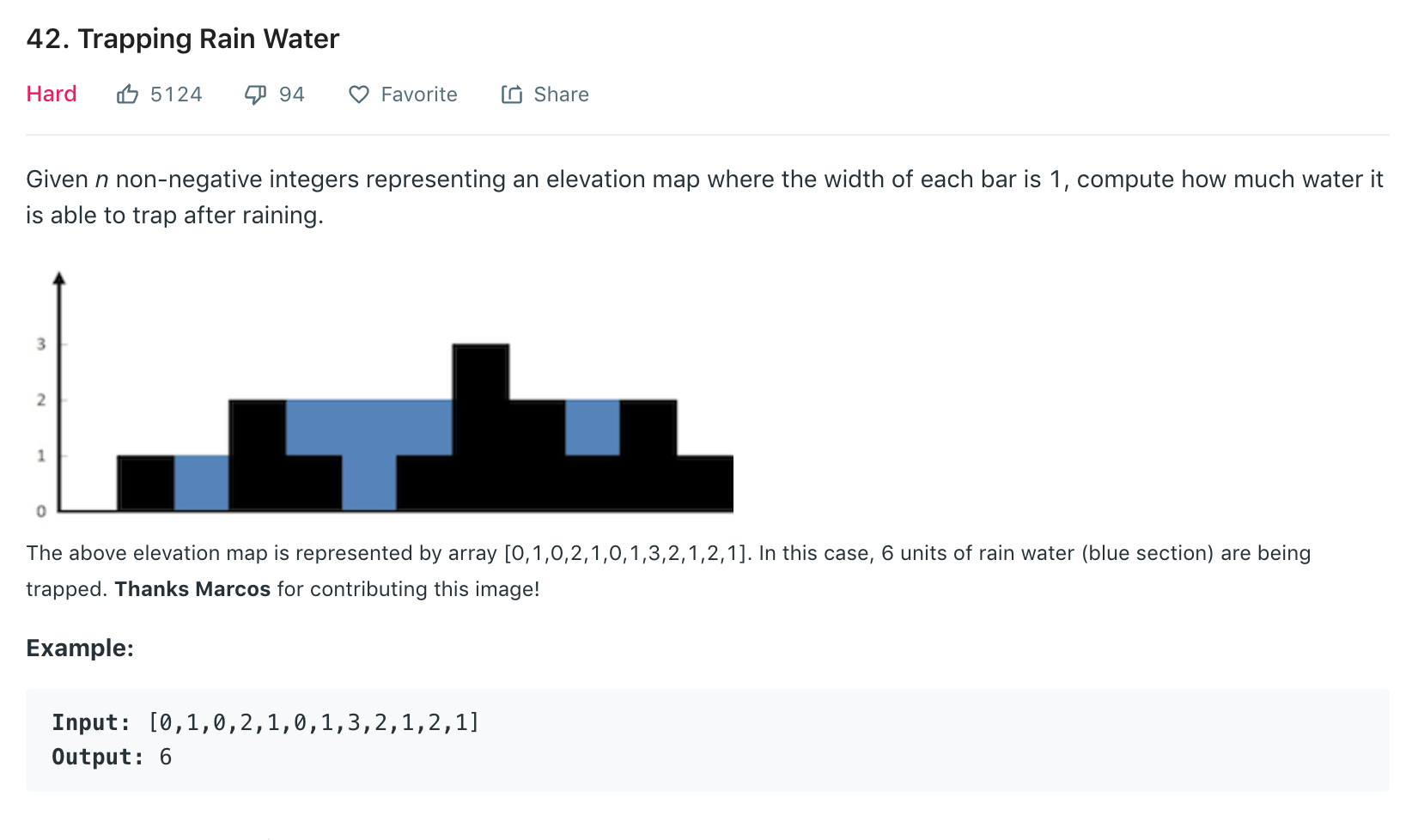
这道题挺有意思的,给定一个非负数的每个宽度为1的柱形图,问你下雨天能接多少雨水。例题中给定的数组能接的总数为6,即图中蓝色部分。
题目分析
我们先来随便举个例子吧。例如示例中给出的数组第6位(也就是索引位置5)高度为0,此时这个位置能盛的水是2。这个2是咋么算出来的呢。从当前位置往它的左边查找,查出最高的水位,即索引3(值为2)。从当前位置往右边找出它的最高位,即索引位置7(值为3),然后取他们中的最小值高度 min(2,3) 减去当前位置的高度(0)=2。为什么取的是两者的最小值呢。很简单的道理,两边之间能盛的水的高度必然会和其中一边高度持平的,再高就溢出了。
代码实现
/**
* @param Integer[] $height
* @return Integer
*/
function trap($height)
{
$res = 0;
$size = count($height);
for ($i = 1; $i < $size - 1; $i++) {
$left = 0;
$right = 0;
for ($j = $i; $j >= 0; $j--) {
$left = max($left, $height[$j]);
}
for ($j = $i; $j < $size; $j++) {
$right = max($right, $height[$j]);
}
$res += min($left, $right) - $height[$i];
}
return $res;
}
你应该已经发现了,上面的执行时间是O(n*n)。每一个位置我们都遍历查找了左右两边,仅仅是为了找最大值,我们为什么不把每个位置左右两边最大值一次存起来?
/**
* @param Integer[] $height
* @return Integer
*/
function trap($height)
{
$res = 0;
$size = count($height);
$left[0] = $height[0];
for ($i = 1; $i < $size; $i++) {
$left[$i] = max($left[$i - 1], $height[$i]);
}
$right[$size - 1] = $height[$size - 1];
for ($i = $size - 2; $i >= 0; $i--) {
$right[$i] = max($right[$i + 1], $height[$i]);
}
for ($i = 1; $i < $size - 1; $i++) {
$res += min($left[$i], $right[$i]) - $height[$i];
}
return $res;
}其实上面的解题思路就是一个动态规划的过程。动态规划最重要的两步:1是状态的定义,即上面的这两个定义:
$left[0] = $height[0];
$right[$size - 1] = $height[$size - 1];第二步就是状态转移方程,即上面的
$left[$i] = max($left[$i - 1], $height[$i]);
$right[$i] = max($right[$i + 1], $height[$i]);
其实动态规划就像是开启了上帝的视角,每次都能获取到全局的情况。经常用来解最优,最近,最少这类题目。你再进一步分析,好像动态规划的思想就是一个空间换时间的方案。第一个解的时间是O(n的平方),空间就一个变量O(1)。再来看第二道解,时间是O(n),空间是O(n)。本质上来说就是空间换时间的方案。最后其实这道题还有其他能解的方案。。。。刷着刷着,乐趣就上来了。
本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu



