AI 知识概论

人工智能概论 -- 人工智能神经及网络，（只记录了重点）

人工智能，它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。

 知识表示✨#

 知识与知识表示的基本概念#

• 知识：把有关信息关联在一起所形成的信息结构在长期的生活及社会实践中、在科学研究及实验中积累起来的对客观世界的认识与经验。

• 任何知识都是在一定的条件及环境下产生的，在这种条件及环境下才是正确的。

• 特性：不确定性

• 随机性、模糊性、不完全性、经验引起

• 特性：可表示性、可利用性

• 知识表示：将人类知识形式化或者模型化。

 通过定义一阶谓词，并通过连接词和量词将一阶谓词组合成谓词公式来描述自然语言所表达的知识#

命题（proposition）：一个非真即假的陈述句。

命题逻辑：研究命题及命题之间关系的符号逻辑系统。

命题逻辑表示法：缺乏抽象能力，不能把不同事物间的共同特征表述出来。

谓词的一般形式：   P (x1, x2,…, xn)

个体 x1, x2,…, xn ：某个独立存在的事物或者某个抽象的概念；

谓词名 P：刻画个体的性质、状态或个体间的关系

表示形式有多种，例如：

- 个体是常量：一个或者一组指定的个体。

“老张是一个教师”：一元谓词 Teacher (Zhang)

“5>3” ：二元谓词 Greater (5, 3)

- 个体是变元（变量）：没有指定的一个或者一组个体。

“x<5” ：Less(x, 5) 

- 个体是函数：一个个体到另一个个体的映射。

“小李的父亲是教师”：Teacher (father (Li) )

谓词公式

连接词（连词）

（1）﹁： “否定” （ negation ）或 “非”。

（2）∨： “析取”（disjunction）—— 或。

（3）∧： “合取”（conjunction）—— 与。

（4）→：“蕴含”(implication) 或 “条件”(condition)。

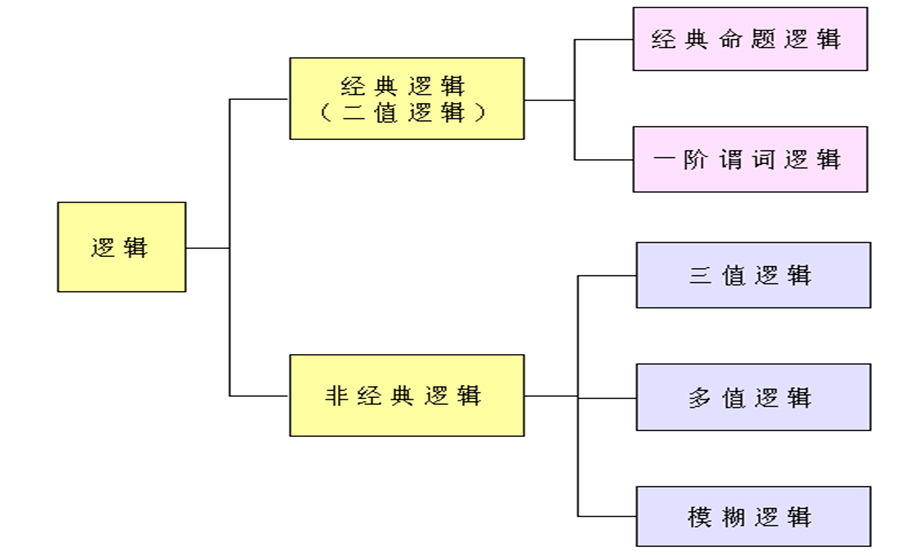
（5）$\leftrightarrow$“等价”（equivalence）或 “双条件” （bicondition）。

量词（quantifier）

（1）全称量词（universal quantifier）：“对个体域中的所有（或任一个）个体 x ”。  

（2）存在量词（existential quantifier）：“在个体域中存在个体 x ”。 

全称量词和存在量词出现的次序将影响命题的意思。

例如：

量词的辖域 

量词的辖域：位于量词后面的单个谓词或者用括弧括起来的谓词公式。

约束变元与自由变元：辖域内与量词中同名的变元称为约束变元，不同名的变元称为自由变元。 

谓词公式

谓词公式的永真性、可满足性、不可满足性、等价性

- 如果谓词公式 P 对个体域 D 上的任何一个解释都取得真值 T，则称 P 在 D 上是永真的；如果 P 在每个非空个体域上均永真，则称 P 永真。  

- 如果谓词公式 P 对个体域 D 上的任何一个解释都取得真值 F，则称 P 在 D 上是永假的；如果 P 在每个非空个体域上均永假，则称 P 永假。

- 对于谓词公式 P，如果至少存在一个解释使得 P 在此解释下的真值为 T，则称 P 是可满足的，否则，则称 P 是不可满足的。

-  设 P 与 Q 是两个谓词公式，D 是它们共同的个体域，若对 D 上的任何一个解释，P 与 Q 都有相同的真值，则称公式 P 和 Q 在 D 上是等价的。如果 D 是任意个体域，则称 P 和 Q 是等价的，记为 P 等价于 Q 。

谓词逻辑的其他推理规则

P 规则：在推理的任何步骤上都可引入前提。

T 规则：在推理过程中，如果前面步骤中有一个或多个公式永真蕴含公式 S，则可把 S 引入推理过程中。

CP 规则：如果能从任意引入的命题 R 和前提集合中推出 S 来，则可从前提集合推出 R → S 来。

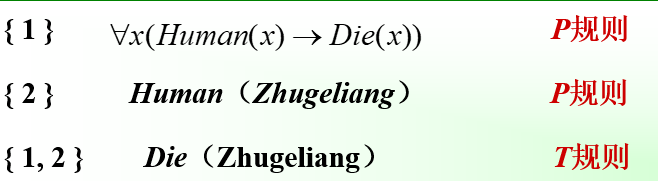
一阶谓词逻辑知识表示方法

用一阶谓词表示：

首先定义谓词  Human (x) 和 Die (x)

然后用连接词连接各个谓词，形成谓词公式。

所有的人都是会死的，

因为诸葛亮是人，       Human（Zhugeliang）

所以诸葛亮是会死的。  Die（Zhugeliang） 

 掌握通过产生式来描述具有因果关系的知识#

确定性规则知识的产生式表示

基本形式：  IF    P    THEN    Q

例如：

r4：IF   动物会飞    AND    会下蛋    THEN   该动物是鸟

2.  不确定性规则知识的产生式表示

基本形式：  IF    P    THEN    Q （置信度） 

或者：                     （置信度）

例如： IF   发烧    THEN    感冒   （0.6）

产生式与谓词逻辑中的蕴含式的区别：

（1）除逻辑蕴含外，产生式还包括各种操作、规则、变换、算子、函数等。例如，“如果炉温超过上限，则立即关闭风门” 是一个产生式，但不是蕴含式。

（2）蕴含式只能表示精确知识，而产生式不仅可以表示精确的知识，还可以表示不精确知识。蕴含式的匹配总要求是精确的。产生式匹配可以是精确的，也可以是不精确的，只要按某种算法求出的相似度落在预先指定的范围内就认为是可匹配的。

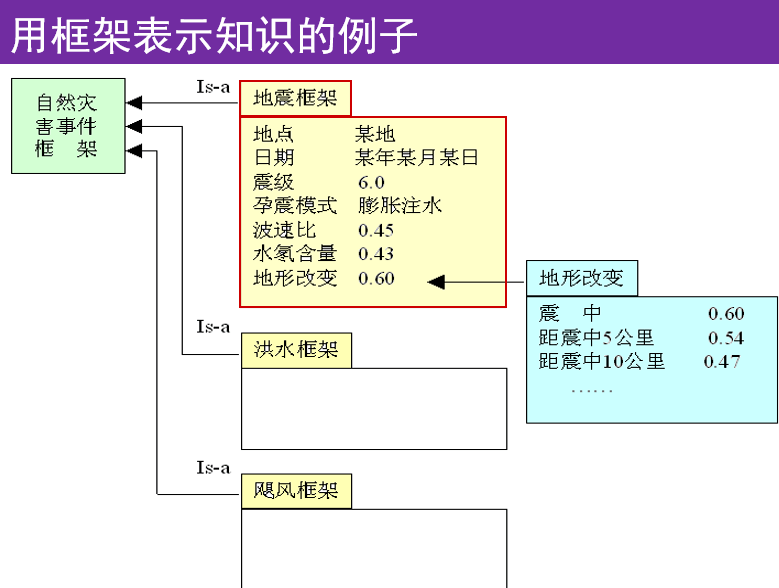
 了解框架表示方法和框架网络；#

框架表示法：一种结构化的知识表示方法，已在多种系统中得到应用。   

框架（frame）：一种描述所论对象（一个事物、事件或概念）属性的数据结构。

一个框架由若干个被称为 “槽”（slot）的结构组成，每一个槽又可根据实际情况划分为若干个 “侧面”（faced）。

一个槽用于描述所论对象某一方面的属性。

一个侧面用于描述相应属性的一个方面。

（1） 结构性 

便于表达结构性知识，能够将知识的内部结构关系及知识间的联系表示出来。 

（2）继承性 

框架网络中，下层框架可以继承上层框架的槽值，也可以进行补充和修改。  

（3）自然性 

框架表示法与人在观察事物时的思维活动是一致的。

槽和侧面所具有的属性值分别被称为槽值和侧面值。

框架名：〈教师 - 1〉

  姓名：李玲

  年龄：39

  性别：女

  职称：副教授

  部门：计算机科学与技术系

  住址：〈adr-1〉

  工资：〈sal-1〉

  开始工作时间：2008，9

  截止时间：2034，4

 确定性推理方法✨#

演绎推理、归纳推理、默认推理

（1）演绎推理 (deductive reasoning) :    一般   →  个别

三段论式（三段论法）

足球运动员的身体都是强壮的 ；

高波是一名足球运动员；

所以，高波的身体是强壮的。

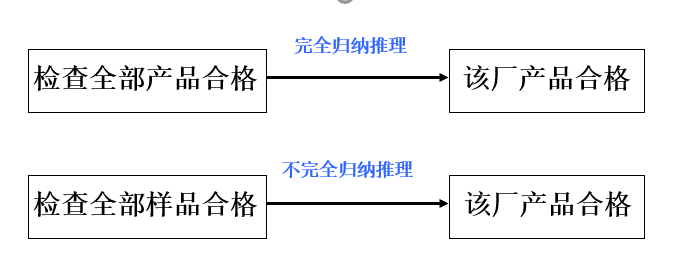
（2）归纳推理 (inductive reasoning):  个别 → 一般

完全归纳推理（必然性推理）              

不完全归纳推理（非必然性推理）

（3）默认推理（default reasoning，缺省推理）

知识不完全的情况下假设某些条件已经具备所进行的推理。

实现正向推理需要解决的问题：

确定匹配（知识与已知事实）的方法。

按什么策略搜索知识库。

冲突消解策略。

正向推理简单，易实现，但目的性不强，效率低。

逆向推理需要解决的问题：

如何判断一个假设是否是证据？

当导出假设的知识有多条时，如何确定先选哪一条？ 

一条知识的运用条件一般都有多个，当其中的一个经验证成立后，如何自动地换为对另一个的验证？

……..

逆向推理：目的性强，利于向用户提供解释，但选择初始目标时具有盲目性，比正向推理复杂。

正向推理:  盲目、效率低。

逆向推理: 若提出的假设目标不符合实际，会降低效率。

正反向混合推理：

（1）先正向后逆向：先进行正向推理，帮助选择某个目标，即从已知事实演绎出部分结果，然后再用逆向推理证实该目标或提高其可信度；

（2）先逆向后正向：先假设一个目标进行逆向推理，然后再利用逆向推理中得到的信息进行正向推理，以推出更多的结论。

在不同谓词公式中，往往会出现谓词名相同但其个体不同的情况，此时推理过程是不能直接进行匹配的，需要先进行代换。

代换（置换）可简单的理解为是在一个谓词公式中用置换项去替换变量。

定义 1 代换（置换）是形如  {t1/x1,t2/x2,…,tn/xn} 的有限集合。其中，t1,t2,…,tn 是项；x1,x2,…,xn 是互不相同的变元；ti/xi 表示用 ti 替换 xi。并且要求 ti 与 xi 不能相同，xi 不能循环地出现在另一个 ti 中。

定义 2 设 θ={t1/x1,t2/x2,…,tn/xn}  λ={ u1/y1, u2/y2, … , um/ym }  是两个代换。则 θ 与 λ 的复合也是一个代换，记作 θ°λ。它是从集合  { t1λ/x1, t2λ/x2, … , tnλ/xn,  u1/y1, u2/y2, … , um/ym } 中删去以下两种元素

① 当 tiλ=xi 时，                       删去 tiλ/xi (i=1, 2 ,…, n)；

② 当 yj∈{ x1, x2 ,…, xn } 时，  删去 uj/yj (j=1, 2 ,…, m)

最后剩下的元素所构成的集合。

合一可理解为是寻找项对变量的置换，使两个谓词公式一致。可定义为：

定义 3 设有公式集 F={F1, F2,…,Fn}，若存在一个置换 θ，可使 F1θ=F2θ=…=Fnθ， 则称 θ 是 F 的一个合一。称 F1,F2,…,Fn 是可合一的。 例如，设有公式集 F={P (x,y,f (y)), P (a,g (x),z)}，则 λ={a/x, g (a)/y, f (g (a))/z} 是它的一个合一。

一般来说，一个公式集的合一不是唯一的。

MGU 算法

（1）初始化，令 k=0, Fk=F,σk=Φ。其中，Φ 是代换空集。

（2）若 Fk 只含一个表达式，则算法停止，σk 就是最一般合一；否则转步骤（3）。

（3）找出 Fk 的差异集 Dk。 

（4）若 Dk 中存在变元 xk 和项 tk，且 xk 不在 tk 中出现，则：

σk+1=σk о  {tk/xk}

Fk+1=Fk {tk/xk}

k=k+1

转步骤（2）；否则， 算法终止，F 的最一般合一不存在。

定义 4 设 σ 是公式集 F 的一个合一，如果对 F 的任一个合一 θ 都存在一个置换 λ，使得 θ=σ°λ，则称 σ 是一个最一般合一。（Most General Unifier）简称 MGU。

一个公式集的最一般合一是唯一的。

MGU 算法

（1）初始化，令 k=0, Fk=F,σk=Φ。其中，Φ 是代换空集。

（2）若 Fk 只含一个表达式，则算法停止，σk 就是最一般合一；否则转步骤（3）。

（3）找出 Fk 的差异集 Dk。 

（4）若 Dk 中存在变元 xk 和项 tk，且 xk 不在 tk 中出现，则：

σk+1=σk о  {tk/xk}

Fk+1=Fk {tk/xk}

k=k+1

转步骤（2）；否则， 算法终止，F 的最一般合一不存在。

例子  设有公式集

F={P(A, x, f  (g (y))),  P(z, f (z), f (u)) }

求其最一般合一。

解：初始化，令 k=0，σ0=Φ，

F0=F={ P (A, x, f (g (y))),  P(z, f (z),  f (u)) }

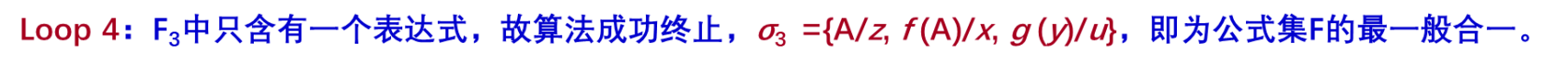
 谓词公式化成子句集的步骤如下：#

(1) 消去连接词 “→” 和 “↔”

反复使用如下等价公式：

P→Q ⇔﹁ P∨Q 

P↔Q ⇔ (P∧Q)∨(﹁P∧﹁Q)

即可消去谓词公式中的连接词 “→” 和 “↔”。

例如公式

(∀x)((∀y)P(x,y)→﹁ (∀y)(Q(x,y)→R(x,y)))

经等价变化后为

(∀x)(﹁(∀y)P(x,y)∨﹁ (∀y)(﹁Q(x,y)∨R(x,y)))

(2) 将否定符号 “﹁” 移到最紧靠谓词的位置

反复使用双重否定定律

﹁(﹁P) ⇔ P

摩根定律

﹁(P∧Q) ⇔﹁P∨﹁Q

﹁(P∨Q) ⇔﹁P∧﹁Q

量词转换律

﹁ (∀x)P(x) ⇔ (∃x) ﹁P(x)

﹁ (∃x)P(x) ⇔ (∀x)￢P(x)

将每个否定符号 “﹁” 移到仅靠谓词的位置，使得每个否定符号最多只作用于一个谓词上。

上式经等价变换后为

(∀x)((∃y)﹁P(x，y)∨(∃y)( Q(x，y) ∧﹁R(x，y)))

(3) 对变元标准化

在一个量词的辖域内，把谓词公式中受该量词约束的变元全部用另外一个没有出现过的任意变元代替，使不同量词约束的变元有不同的名字。

例如，上式经变换后为

(∀x)((∃y)﹁P(x，y)∨(∃z)( Q(x，z) ∧﹁R(x，z)))

(4) 化为前束范式

化为前束范式的方法：把所有量词都移到公式的左边，并且在移动时不能改变其相对顺序。由于第 (3) 步已对变元进行了标准化，每个量词都有自己的变元，这就消除了任何由变元引起冲突的可能，因此这种移动是可行的。

例如，上式化为前束范式后为

(∀x)(∃y) (∃z)(﹁P(x，y)∨( Q(x，z) ∧﹁R(x，z)))

(5) 消去存在量词

消去存在量词时，需要区分以下两种情况：

若存在量词不出现在全称量词的辖域内

（即它的左边没有全称量词），只要用一个新的个体常量替换受该存在量词约束的变元，就可消去该存在量词。

若存在量词位于一个或多个全称量词的辖域内

例如

(∀x1)…(∀xn) (∃y)P(x1，x2 ,…, xn ,y)

则需要用 Skolem 函数 f (x1，x2 ,…, xn) 替换受该存在量词约束的变元 y，然后再消去该存在量词。

例如，上步所得公式中存在量词 (∃y) 和 (∃z) 都位于 (∀x) 的辖域内，因此都需要用 Skolem 函数来替换。设替换 y 和 z 的 Skolem 函数分别是 f (x) 和 g (x)，则替换后的式子为

(∀x)(﹁P(x,f(x))∨ (Q(x,g(x))∧﹁ R(x,g(x)) ) )

(6) 化为 Skolem 标准形

Skolem 标准形的一般形式为

(∀x1)…(∀xn) M(x1,x2,……,xn)

其中， M (x1,x2,……,xn) 是 Skolem 标准形的母式，它由子句的合取所构成。把谓词公式化为 Skolem 标准形需要使用以下等价关系

P∨(Q∧R) ⇔ (P∨Q)∧(P∨R)

例如，前面的公式化为 Skolem 标准形后为

(∀x)((﹁P(x,f(x))∨Q(x,g(x))∧(﹁P(x,f(x))∨﹁R(x,g(x))))

(7) 消去全称量词

由于母式中的全部变元均受全称量词的约束，并且全称量词的次序已无关紧要，因此可以删掉全称量词。但剩下的母式，仍假设其变元是被全称量词量化的。

例如，上式消去全称量词后为

(﹁P(x,f(x))∨Q(x,g(x)) ∧(﹁P(x,f(x))∨﹁R(x,g(x)))

(8) 消去合取词

在母式中消去所有合取词，把母式用子句集的形式表示出来。其中，子句集中的每一个元素都是一个子句。

例如，上式的子句集中包含以下两个子句

{  ﹁P(x,f(x))∨Q(x,g(x))

﹁P(x,f(x))∨﹁R(x,g(x)) }

(9) 更换变量名称

对子句集中的某些变量重新命名，使任意两个子句中不出现相同的变量名。由于每一个子句都对应着母式中的一个合取元，并且所有变元都是由全称量词量化的，因此任意两个不同子句的变量之间实际上不存在任何关系。这样，更换变量名是不会影响公式的真值的。

例如，对前面的公式，可把第二个子句集中的变元名 x 更换为 y，得到如下子句集

﹁P(x,f(x))∨Q(x,g(x))

﹁P(y,f(y))∨﹁R(y,g(y))

例子：

 掌握归结原理；#

归结原理基本思想

首先把欲证明问题的结论否定，并加入子句集，得到一个扩充的子句集 S’。然后设法检验子句集 S’是否含有空子句，若含有空子句，则表明 S’是不可满足的；

若不含有空子句，则继续使用归结法，在子句集中选择合适的子句进行归结，直至导出空子句或不能继续归结为止。

归结原理包括

命题逻辑归结原理

谓词逻辑归结原理

命题归结原理和归结树：

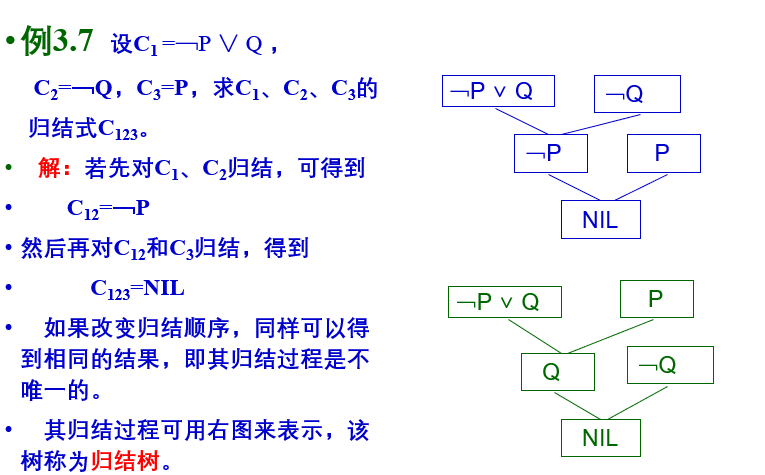
谓词归结和归结树：

谓词逻辑的归结原理

谓词逻辑中的归结式可用如下定义来描述：

定义 3  设 C1 和 C2 是两个没有公共变元的子句，L1 和 L2 分别是 C1 和 C2 中的文字。如果 L1 和 L2 存在最一般合一 σ，则称

C12=({C1σ}-{ L1σ})∪({ C2σ}-{ L2σ})

为 C1 和 C2 的二元归结式，而 L1 和 L2 为归结式上的文字

 能够利用归结反演进行问题求解；#

例子：

下面再通过一个例子来说明如何求取问题的答案。

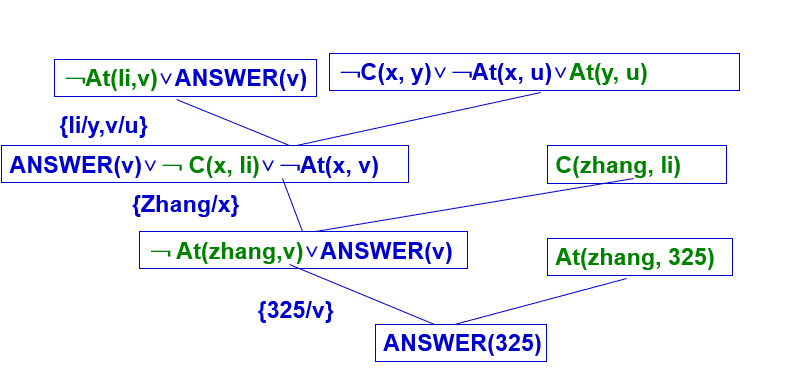
例子  已知：“张和李是同班同学，如果 x 和 y 是同班同学，则 x 的教室也是 y 的教室，现在张在 325 教室上课。” “现在李在哪个教室上课？” 

C (x, y)     x 和 y 是同班同学；

At (x, u)    x 在 u 教室上课。

把已知前提用谓词公式表示如下： C (zhang, li) (∀x) (∀y) (∀u) (C (x, y)∧At (x, u)→At (y,u)) At (zhang, 325)   

把目标的否定用谓词公式表示如下： ﹁(∃v) At (li, v)    

把上述公式化为子句集： 

C(zhang, li)

﹁C(x, y)∨﹁At(x, u)∨At(y, u)

At(zhang, 325)

把目标的否定化成子句式，

﹁At (li,v) ∨ANSWER (v)         代替之。

把此重言式加入前提子句集中，得到一个新的子句集，对这个新的子句集，应用归结原理求出其证明树。其求解过程如下图所示。

该证明树的根子句就是所求的答案，即 “李明在 325 教室”。

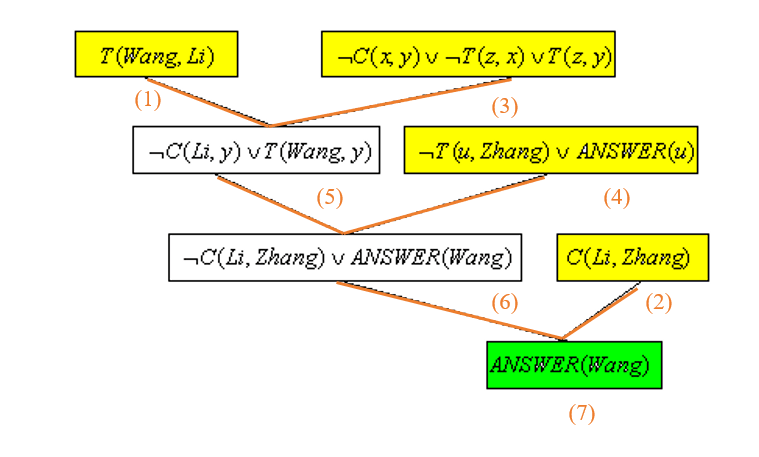
例子 2：

归结树：

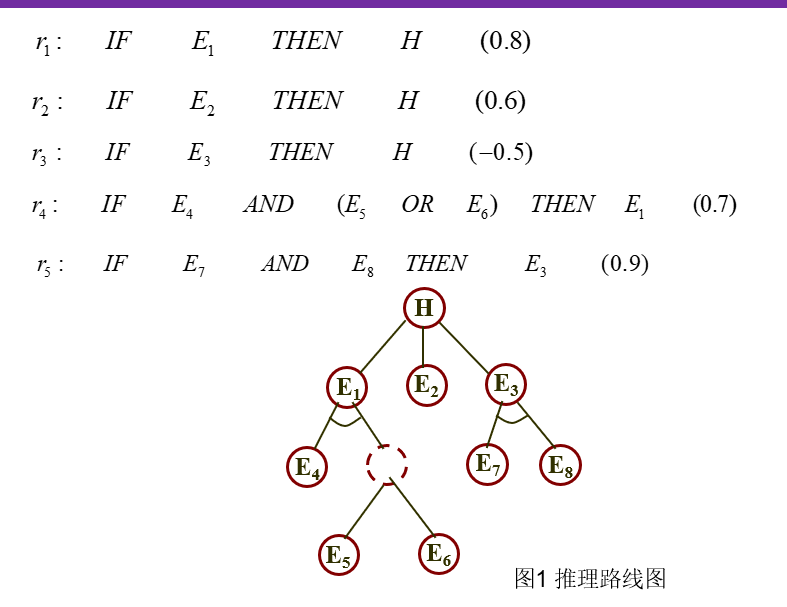
 不确定性推理方法、掌握可信度方法#

（1）确定性推理：推理时所用的知识与证据都是确定的，推出的结论也是确定的，其真值或者为真或者为假。 

（2）不确定性推理：推理时所用的知识与证据不都是确定的，推出的结论也是不确定的。

不确定性推理：从不确定性的初始证据出发，通过运用不确定性的知识，最终推出具有一定程度的不确定性但却是合理或者近乎合理的结论的思维过程。

- 

可信度：根据经验对一个事物或现象为真的相信程度。

可信度带有较大的主观性和经验性，其准确性难以把握。

C－F 模型：基于可信度表示的不确定性推理的基本方法。   

不确定性的表示

（1）知识不确定性的表示

CF（H，E）的取值范围: [-1,1]。

若由于相应证据的出现增加结论 H 为真的可信度，则 CF（H，E）> 0，证据的出现越是支持 H 为真，就使 CF（H，E) 的值越大。

反之，CF（H，E）< 0，证据的出现越是支持 H 为假，CF（H，E）的值就越小。

若证据的出现与否与 H 无关，则 CF（H，E）= 0。

（2）证据不确定性的表示 —— 证据的动态强度

静态强度 CF（H，E）：知识的强度，即当 E 所对应

的证据为真时对 H 的影响程度。

动态强度 CF（E）：证据 E 当前的不确定性程度。

（3）组合论据：

传递性：

合成算法的计算方法：

例子：

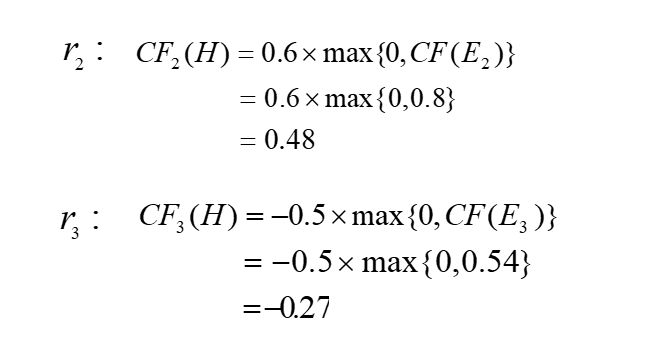
不确定性的度量   

① 能充分表达相应知识及证据不确定性的程度。

② 度量范围的指定便于领域专家及用户对不确定性的估计。

③ 便于对不确定性的传递进行计算，而且对结论算出的不确定性量度不能超出量度规定的范围。

④ 度量的确定应当是直观的，同时应有相应的理论依据。 

 了解证据理论方法。#

目前，在证据理论的基础上已经发展了多种不确定性推理模型。

1 概率分配函数

如果 ，则正交和 M 也是一个概率分配函数；

如果 ，则不存在正交和 M，即没有可能存在概率函数，称 与 矛盾。
K 和 M 的计算

信任函数和似然函数：

4 概率分配函数的正交和（证据的组合）

5 基于证据理论的不确定性推理

 搜索策略✨#

依靠经验，利用已有知识，根据问题的实际情况，不断寻找可利用知识，从而构造一条代价最小的推理路线，使问题得以解决的过程称为搜索

 掌握搜索问题形式化表示，重点掌握状态空间表示法和与或树表示法；#

-  按问题的表示方式

状态空间搜索 (State Space) 

与或树搜索 (And/Or Tree)

按是否使用启发式信息

盲目搜索（Blind Search）

启发式搜索 (Heuristic Search)

 重点掌握状态空间表示法 和 与或树表示法、了解状态空间盲目搜索方法；#

状态空间表示法用 “状态” 和 “算符” 来表示问题

状态 — 描述问题求解过程不同时刻的状态

算符 — 表示对状态的操作

算符的每一次使用就使状态发生变化。当到达目标状态时，由初始状态到目标状态所使用的算符序列就是问题的一个解。

①状态：是描述问题求解过程不同时刻的状态的数据结构，可用一组变量的有序集表示：

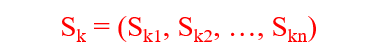
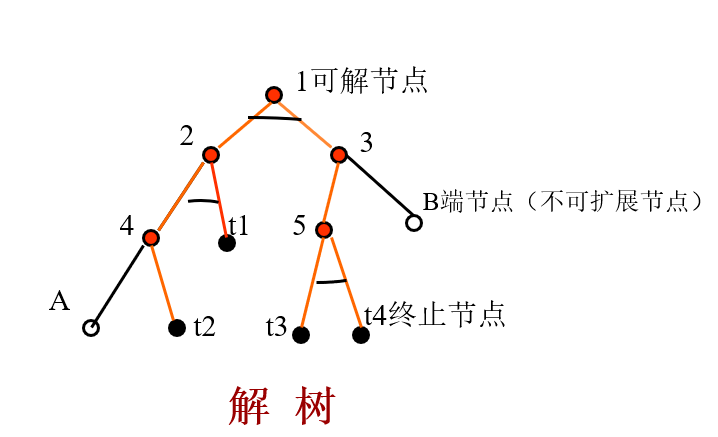
与或树表示法：

本原问题

不能再分解或变换，而且可以直接可解的子问题称为本原问题。

端节点与终止节点

在与 / 或树中，没有子节点的节点称为端节点；本原问题所对应的节点称为终止节点。可见，终止节点一定是端节点，而端节点不一定是终止接点。

可解节点

在与 / 或树中，满足下列条件之一者，称为可解节点：

1) 它是一个终止节点。

2) 它是一个 “或” 节点，且其子节点至少有一个是可解节点。

3) 它是一个 “与” 节点，且其子节点全部是可解节点。

不可解节点

关于可解节点的三个条件全部不满足的节点称为不可解节点。

解树

由可解节点所构成的，并且由这些可解节点可推出初始节点为可解节点的子树称为解树。

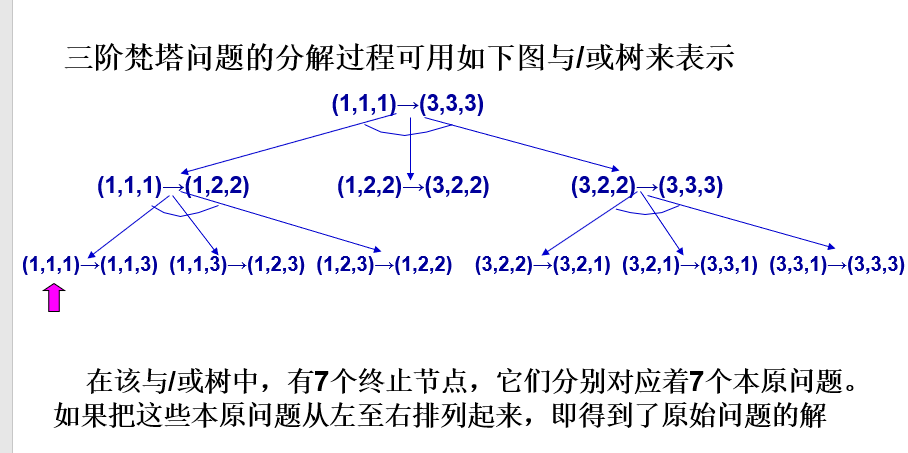
三阶梵塔问题。

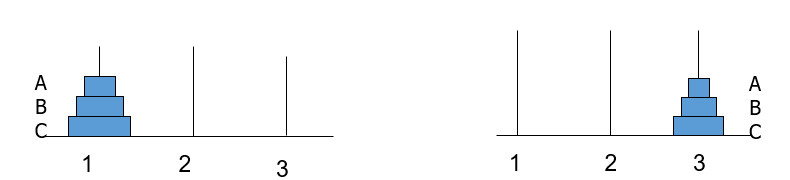
当给每一个分量以确定的值时，就得到了一个具体的状态

②算符：引起状态中某些分量发生变化，从而使问题由一个状态变为另一个状态的操作称为算符。在产生式系统中，每一条产生式规则就是一个算符

③状态空间：

由问题的全部状态及一些可用算符所构成的集合称为问题的状态空间，一般用一个三元组表示：

(S, F, G)    其中 S 是问题的所有初始状态构成的集合；F 是算符的集合；G 是目标状态的集合。

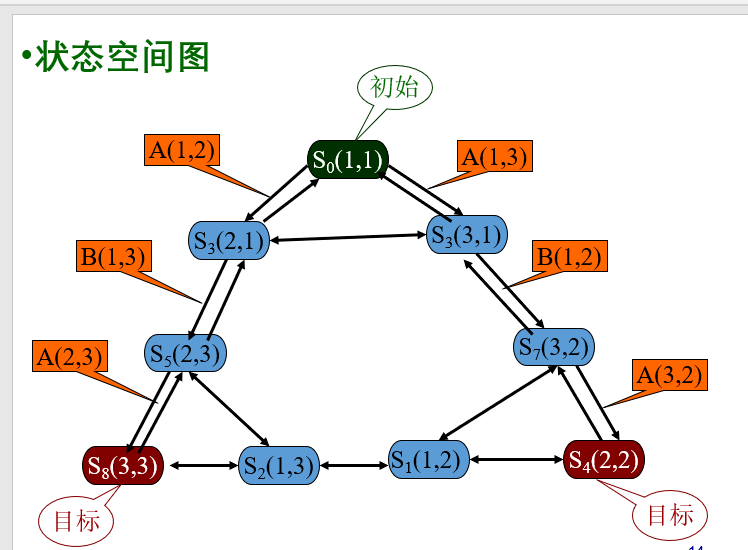
④状态空间图

状态空间的图示形式称为状态空间图。其中节点表示状态；有向边表示算符。

例子：

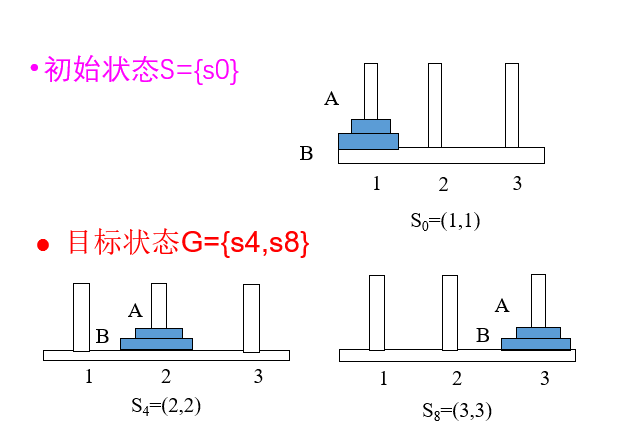
二阶 “梵塔” 问题状态空间表示

有三个柱子 (1，2，3) 和两个不同尺寸的圆盘 (A，B)。在每个圆盘的中心有个孔，所以圆盘可以堆叠在柱子上，最初，全部两个圆盘都堆在柱子 1 上 (最大的在底部，最小的在顶部)。要求把所有 圆盘都移到另一个柱子上，搬动规则为:

(1) 一次只能搬一个圆盘

(2) 不能将大圆盘放在小圆盘

(3) 可以利用空柱子。

如何用状态空间方法来描述问题？

状态的表示

柱子的编号用 i,j 来代表 (i,j) 表示问题的状态其中: i 代表 A 所在的柱子

j 代表 B 所在的柱子

状态集合 (9 种可能的状态)

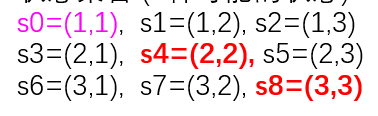
算符如何定义？

定义算符 A (i,j) 表示把 A 从 i 移到 j；

  B (i,j) 表示把 B 从 i 移到 j。

算符集合 (共 12 个算符）： 

A(1,2),A(1,3),A(2,1),A(2,3),A(3,1),A(3,2)

B(1,2),B(1,3),B(2,1),B(2,3),B(3,1),B(3,2)

- 掌握 OPEN 表和 CLOSE 表的构成及作用；

1、特点：

1) 搜索按规定的路线进行，不使用与问题有关的启发性信息

2) 适用于其状态空间图是树状结构的问题求解。

2、搜索过程：

一般都要用两个表，这就是 OPEN 表和 CLOSED 表。  

OPEN 表用于待考察的节点。

CLOSED 表用于存放已考察的节点。

3、当目标状态出现的时候，结束搜索。

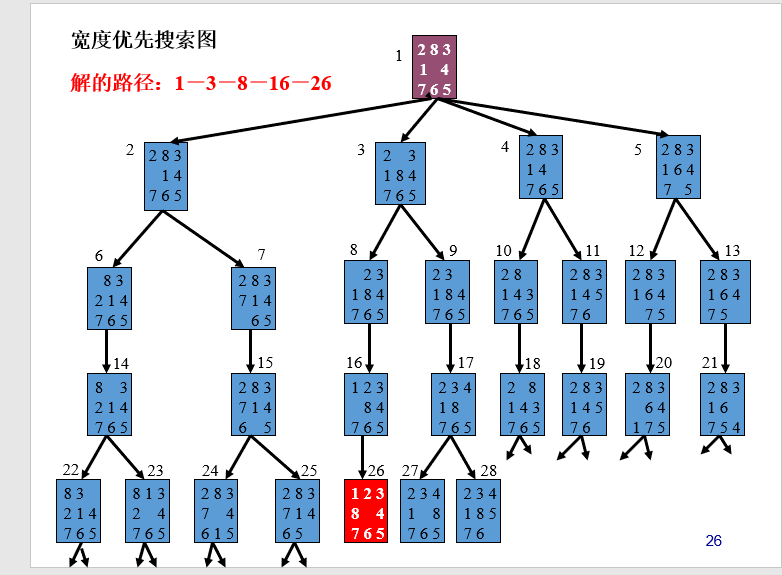
对于上图的空间状态我们列出所有可能的 open 表：

Open 表的变化 (宽度优先搜索）     初始 (1)

1     (2,3,4,5)

2     (3,4,5,6,7)

3     (4,5,6,7,8,9)

4     (5,6,7,8,9,10,11)

5     (6,7,8,9,10,11,12,13)

6     (7,8,9,10,11,12,13,14)

7     (8,9,10,11,12,13,14,15,)

8     (9,10,11,12,13,14,15,16)

9     (10,11,12,13,14,15,16,17)

10   (11,12,13,14,15,16,17,18)

11   (12,13,14,15,16,17,18,19)

12   (13,14,15,16,17,18,19,20)

13   (14,15,16,17,18,19,20,21)

14   (15,16,17,18,19,20,21,22,23)

15   (16,17,18,19,20,21,22,23,24,25)

16   (17,18,19,20,21,22,23,24,25,26) 

..      …        ….       … ……

25   (26,27,28,…………………………)

26   找到目标节点。

宽度优先搜索改进：

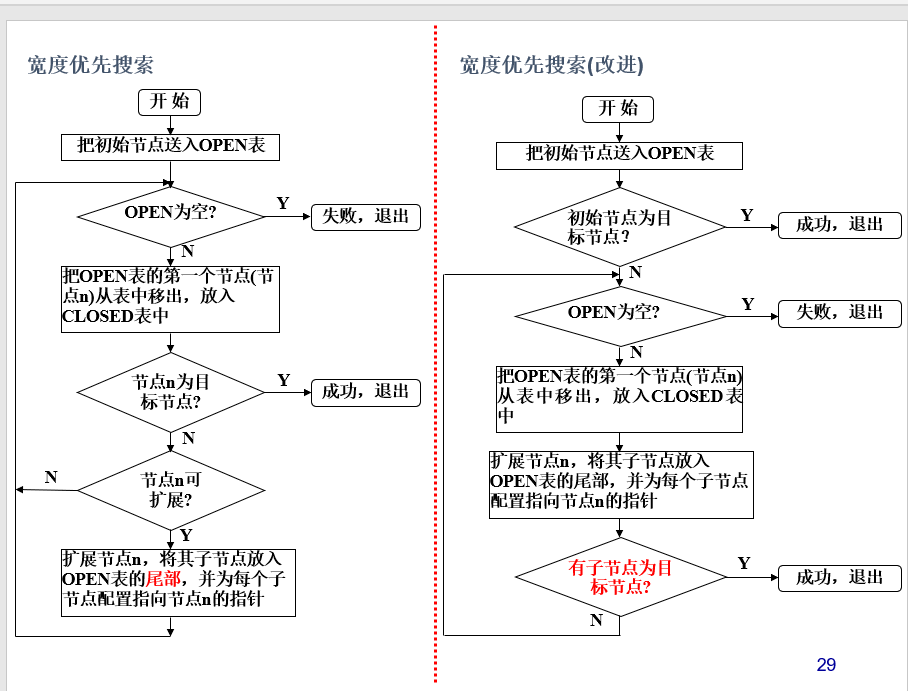
Open 表的变化 (改进的宽度优先搜索）

初始 (1)

1     (2,3,4,5)

2     (3,4,5,6,7)

3     (4,5,6,7,8,9)

4     (5,6,7,8,9,10,11)

5     (6,7,8,9,10,11,12,13)

6     (7,8,9,10,11,12,13,14)

7     (8,9,10,11,12,13,14,15,)

8     (9,10,11,12,13,14,15,16)

9     (10,11,12,13,14,15,16,17)

10   (11,12,13,14,15,16,17,18)

11   (12,13,14,15,16,17,18,19)

12   (13,14,15,16,17,18,19,20)

13   (14,15,16,17,18,19,20,21)

14   (15,16,17,18,19,20,21,22,23)

15   (16,17,18,19,20,21,22,23,24,25)

16   (17,18,19,20,21,22,23,24,25,)                 

26 为 16 的子节点，是目标节点，得到解

深度优先传统算法和改进算法：

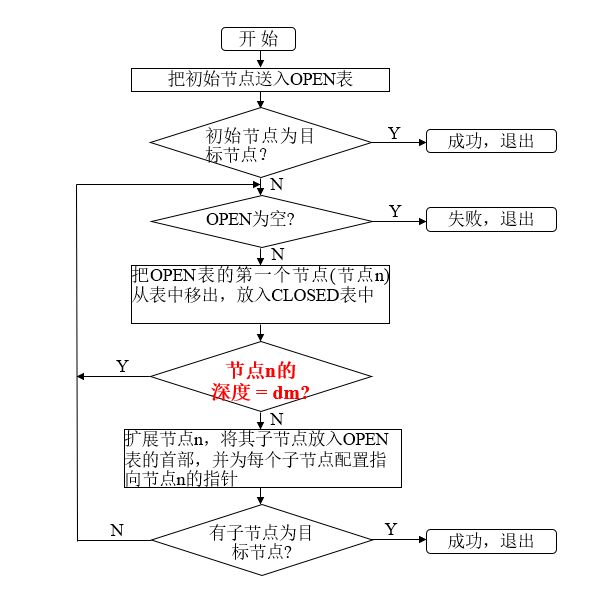
存在问题：

1、dm 的值很难给出。

2、不能保证找到最优解。

改进方法：

可变深度

可变深度的思想：

基本思想：先任意给定一个较小的数作为 dm，然后进行上述的有界深度优先搜索，当搜索到达了指定的深度界限 dm 仍未发现目标节点，并且 CLOSED 表中仍有待扩展节点时，就将这些节点送回 OPEN 表，同时增大深度界限 dm 继续向下搜索。如此不断地增大 dm，只要问题有解，就一定可以找到它。

 掌握状态空间启发式搜索和估价函数的设计方法，深入理解启发式函数；#

启发性信息 —— 可用于指导搜索过程，且与具体问题求解有关的控制性信息。

用于估计节点的重要性的函数称为估计函数。其一般形式为：

f(x) = g(x) + h(x)

其中 g (x) 为从初始节点 S0 到节点 x 已经实际付出的代价；h (x) 是从节点 x 到目标节点 Sg 的最优路径的估计代价， h (x) 称为启发函数，它体现了问题的启发性信息。

定义启发函数要根据具体问题具体分析，可以参考的思路有：

　①　一个结点到目标结点的某种距离或差异的度量； 

　②　一个结点处在最佳路径上的概率； 

　③　根据经验主观打分 

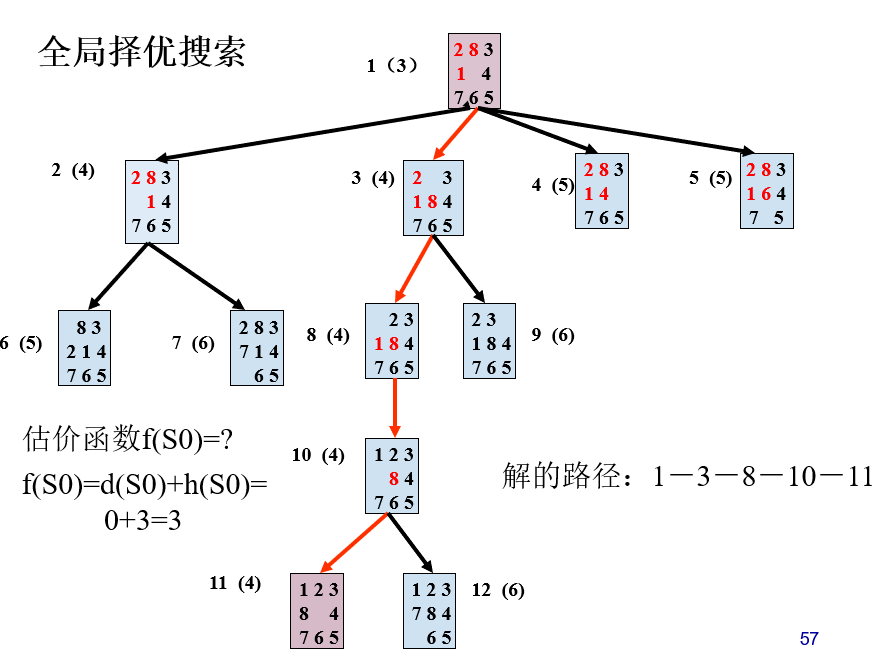
全局择优搜索

每次总是从 OPEN 表的全体节点中选择一个估价值最小的节点。

过程如下：

(1) 把初始节点 S0 放入 OPEN 表，f (S0)。

(2) 如果 OPEN 表为空，则问题无解，退出。

(3) 把 OPEN 表的第一个节点 (记为节点 n) 取出放入 CLOSED 表。

(4) 考察节点 n 是否为目标节点。若是，则求得问题的解，退出。

(5) 若节点 n 不可扩展，则转第 (2) 步。

(6) 扩展节点 n，用估计函数 f (x) 计算每个子节点的估价值，并为每个子节点配置指向父节点的指针，把这些子节点都送入 OPEN 表中，然后对 OPEN 表中的全部节点按估价值从小到大的顺序进行排序，然后转第 (2) 步。

前面讨论的择优搜索仅适合于搜索的状态空间是树状结构，树状结构的状态空间中每个节点都只有唯一的父节点 (根节点除外)。因此搜索算法放入到 OPEN 表中的节点的状态是各不相同的，不会有重复的节点。

如果状态空间是一个有向图的话，那么状态空间中的一个节点可能有多个父节点，因此，在 OPEN 表中会出现重复的节点，节点的重复将导致大量的冗余搜索，为此须对全局择优搜索进行修正。

修正的思想：当搜索过程生成一个节点 i 时，需要把节点 i 的状态与已生成的所有节点的状态进行比较，若节点 i 是一个已生成的节点，则表示找到一条通过节点 i 的新路径。若新路径使节点 i 的估价值更小，则修改节点 i 指向父节点的指针，使之指向新的父节点；否则，不修改节点 i 原有的父节点指针，即保留节点 i 原有的路径

* 有序搜索（A 算法）、A 算法 **

h(n) 就是从 n 到目标节点路径的最小代价；函数 g(n) 是所有从 S 开始可达到 n 的路径的最小代价；函数 f(n) 就是从节点 S 到节点 n 的一条最佳路径的实际代价加上从节点 n 到某目标节点的一条最佳路径的代价之和，即 f(n)=g(n)+ h(n)

我们希望估价函数 f (n) 是 f(n) 的一个估计，此估计可由下式给出：　　　　f (n)=g (n)+h (n)　　其中：g 是 g 的估计；h 是 h 的估计。对于 g (n) 来说。很显然 g (n)≥g(n)。对于 h*(n) 估计 h (n)，它依赖于有关问题的领域的启发信息。 

定义 1 ：在 GRAPHSEARCH 过程中，如果重排 OPEN 表是依据 f (x)=g (x)+h (x) 进行的，则称该过程为 A 算法。

定义 2 ：在 A 算法中，如果对所有的 x，h (x)≤h(x) 成立，则称 h (x) 为 h(x) 的下界，它表示某种偏于保守的估计。

基于上述 g(x) 和 h(x) 的定义，对启发式搜索算法中的 g (x) 和 h (x) 做如下限制：

①g (x) 是对 g*(x) 的估计，且 g (x)>0；

②h (x) 是 h(x) 的下界，即对任意节点 x 均有 h (x)≤h(x)。

在满足上述条件情况下的有序搜索算法称为 A * 算法。

对于某一搜索算法，当最佳路径存在时，就一定能找到它，则称此算法是可纳的。可以证明，A 算法是可纳算法。也就是说，对于有序搜索算法，当满足 h (x)≤h(x) 条件时，只要最佳路径存在，就一定能找出这条路径。

 了解与或树盲目搜索#

与或树搜索基本思想：

扩展（自上而下）

标示（自下而上）

结束条件：初始节点为可解或不可解

与或树盲目搜索

宽度优先

深度优先

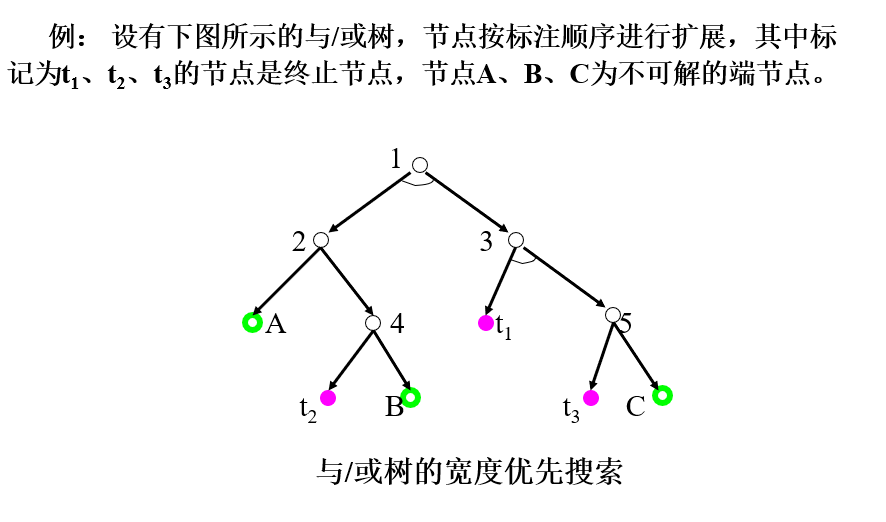
与 / 或树的宽度优先搜索与状态空间的宽度优先搜索类似，是按

“先产生的节点先扩展” 的原则进行搜索，只是在搜索过程中要多次调用可解标示过程和不可解标示过程。搜索过程如下：

(1) 把初始节点 S0 放入 OPEN 表。

(2) 把 OPEN 表中的第一个节点 (记为节点 n) 取出放入 CLOSED 表。

(3) 如果节点 n 可扩展，则：

　① 扩展节点 n，将其子节点放入 OPEN 表的尾部，并为每个子节点配置指向父节点的指针。

　② 考察这些子节点中是否有终止节点。若有，则标示这些终止节点为可解节点，并应用可解标示过程对其先辈节点中的可解节点进行标示。如果初始节点 S0 也被标示为可解节点，就得到了解树，搜索成功，退出搜索过程；如果不能确定 S0 为可解节点，则从 OPEN 表中删去具有可解先辈的节点。

　③ 转第 (2) 步。

(4) 如果节点 n 不可扩展，则：

　① 标示节点 n 为不可解节点。

　② 应用不可解标示过程对节点 n 的先辈节点中不可解的节点进行标示。如果初始节点 S0 也被标示为不可解节点，则搜索失败，表明原始问题无解，退出搜索过程；如果不能确定 S0 为不可解节点，则从 OPEN 表中删去具有不可解先辈的节点

　③ 转第 (2) 步。

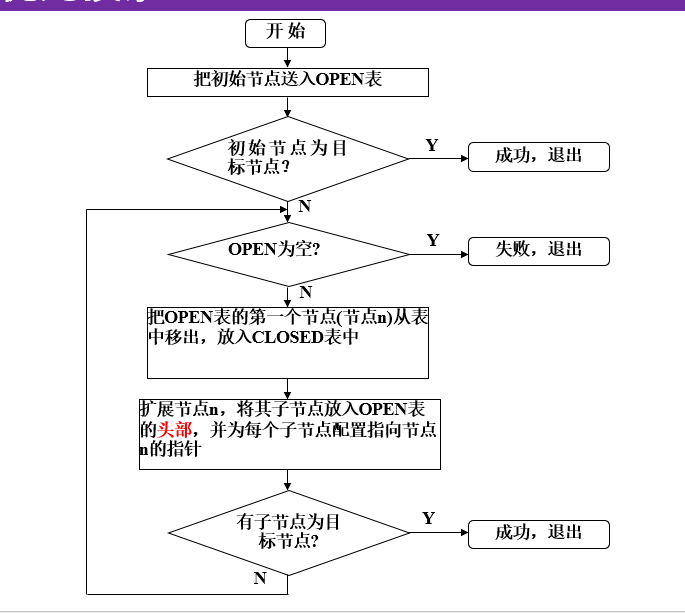
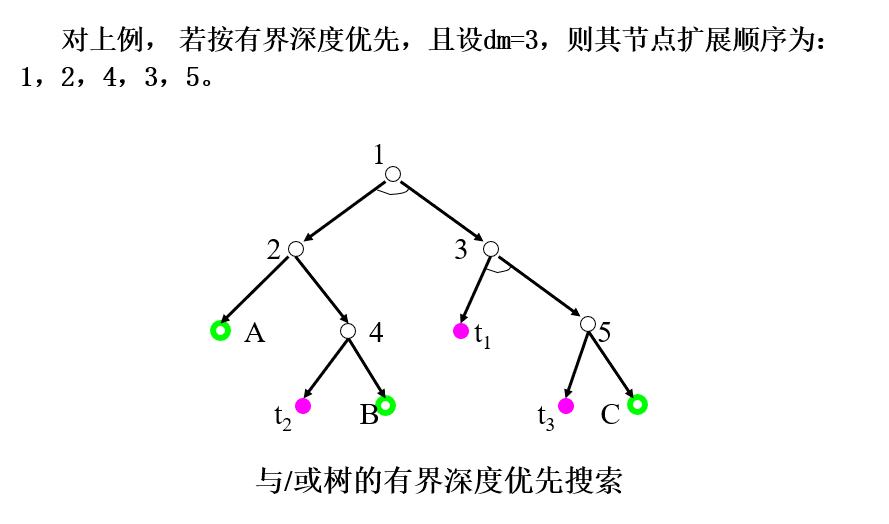
深度优先搜索：

搜索过程如下：

(1) 把初始节点 S0 放入 OPEN 表。

(2) 把 OPEN 表中的第一个节点 (记为节点 n) 取出放入 CLOSED 表。

(3) 如果节点 n 的深度大于等于深度界限，则转第 5) 步的第①点

(4) 如果节点 n 可扩展，则：

　① 扩展节点 n，将其子节点放入 OPEN 表的头部，并为每个子节点配置指向父节点的指针。

　② 考察这些子节点中是否有终止节点。若有，则标示这些终止节点为可解节点，并应用可解标示过程对其先辈节点中的可解节点进行标示。如果初始节点 S0 也被标示为可解节点，就得到了解树，搜索成功，推出搜索过程；如果不能确定 S0 为可解节点，则从 OPEN 表中删去具有可解先辈的节点。

　③ 转第 (2) 步。

(5) 如果节点 n 不可扩展，则：

　① 标示节点 n 为不可解节点。

　② 应用不可解标示过程对节点 n 的先辈节点中不可解的节点进行标示。如果初始节点 S0 也被标示为不可解节点，则搜索失败，表明原始问题无解，退出搜索过程；如果不能确定 S0 为不可解节点，则从 OPEN 表中删去具有不可解先辈的节点

　③ 转第 (2) 步。

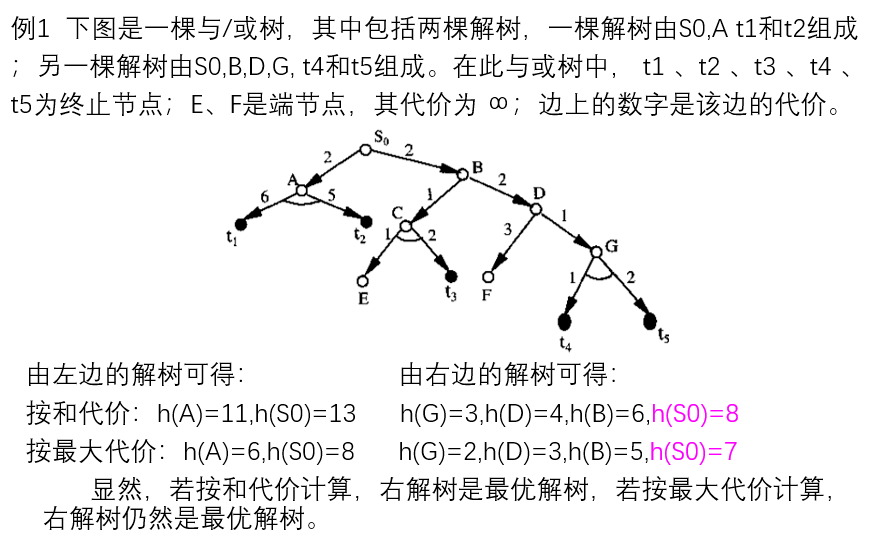
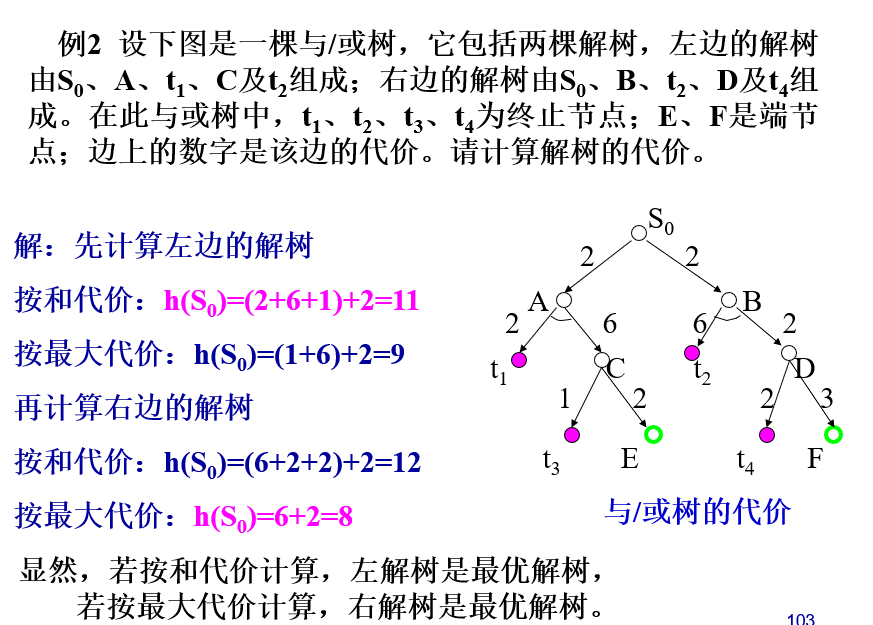
 掌握解树代价的求取，理解利用希望树求取代价最小解树的方法；#

与 / 或树的启发式搜索可用来求取代价最小的解树，也被称之为与或树有序搜索。

为了进行有序搜索，需要计算解树的代价。解树的代价可以通过计算解树中节点的代价得到。

1) 如果 x 是终止节点，则定义节点 x 的代价 h (x) = 0；

2) 如果 x 是” 或” 节点，y1,y2…yn 是它的子节点，则节点 x 的代价为：h (x) = min {c (x,yi) + h (yi)}

3) 如果 x 是” 与” 节点，则节点 x 的代价有两种计算方法：和代价法与最大代价法。

若按和代价法计算，则有：h (x) = ∑(c (x,yi) + h (yi)) 若按最大代价法计算，则有：h (x) = max {c (x,yi) + h (yi)}

4) 如果 x 不可扩展，且又不是终止节点，则定义 h (x) = ∝

　由上述计算节点的代价可以看出，如果问题是可解的，则由子节点的代价就可推算出父节点代价，这样逐层上推，最终就可求出初始节点 S0 的代价，S0 的代价就是解树的代价。

2、希望树

希望树是指搜索过程中最有可能成为最优解树的那棵树。

与 / 或树的启发式搜索过程就是不断地选择、修正希望树的过程，在该过程中，希望树是不断变化的。

定义：   

(1) 初始节点 S0 在希望树 T 

(2) 如果 n 是具有子节点 n1, n2, … , nk 的或节点，则 n 的某个子节点 ni 在希望树 T 中的充分必要条件是 

(3) 如果 n 是与节点，则 n 的全部子节点都在希望树 T 中。

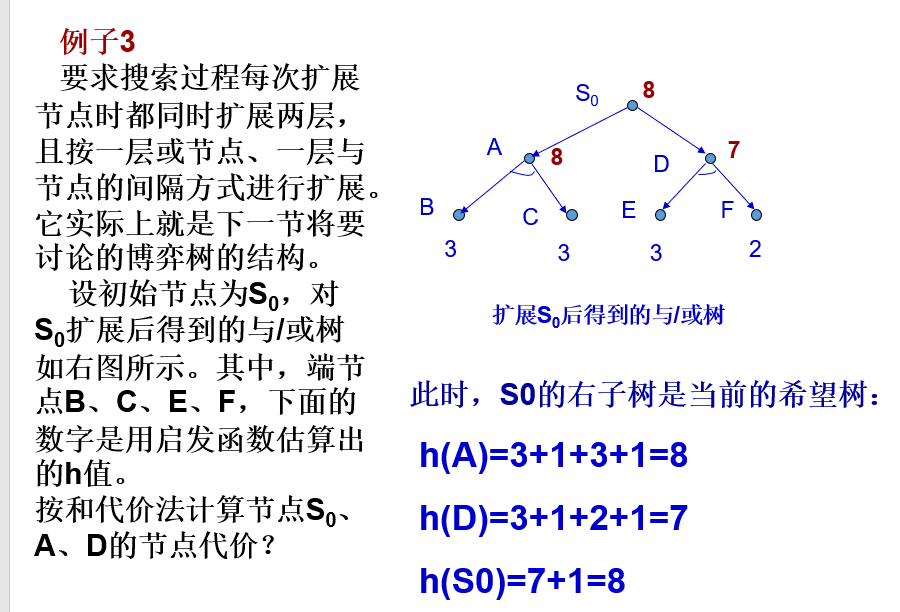
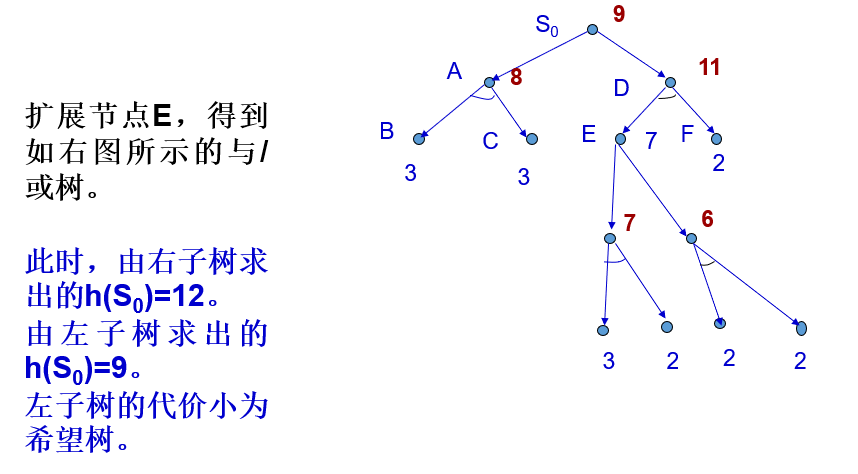
 掌握基于极大极小方法的博弈树搜索及 alpha-beta 剪枝策略。#

博弈问题特点

全信息：对垒的双方 A，B 轮流采取行动，任何一方都了解当前的格局及过去的历史。

二人零和：博弈的结果只有三种情况：A 方胜，B 方败；B 方胜，A 方败；双方战成平局。

非偶然：博弈的过程是寻找置对手于必败状态的过程。

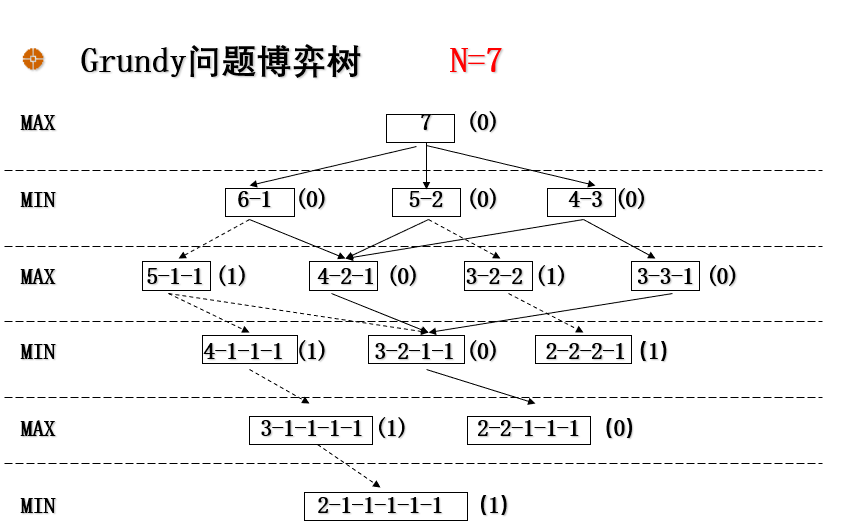
Grundy 博弈是一个分钱币的游戏。有一堆数目为 N 的钱币，由两位选手轮流进行分堆，要求每个选手每次只把其中某一堆分成数目不等的两小堆。例如， 选手甲把 N 分成两堆后，轮到选手乙就 可以挑其中一堆来分，如此进行下去， 直到有一位选手先无法把钱币再分成不相等的两堆时就得认输。

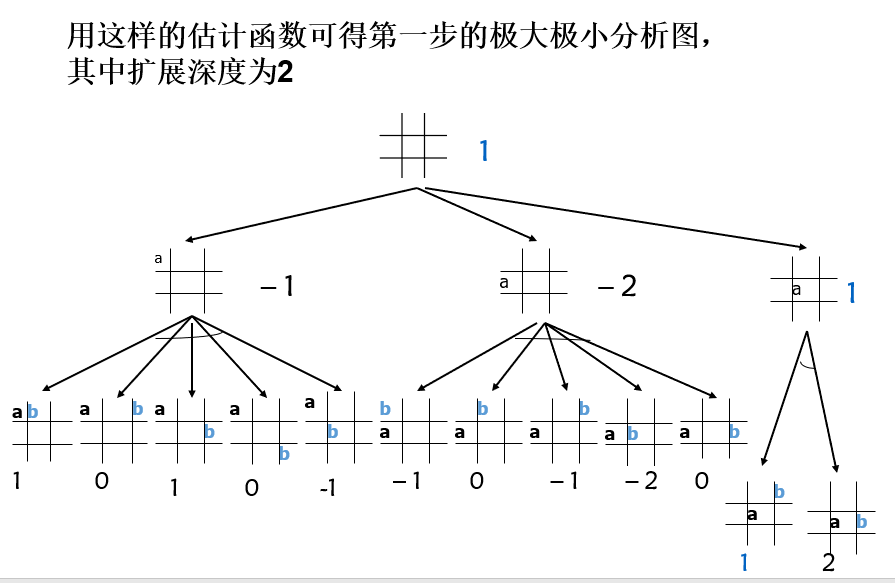
极大极小分析法的基本思想

设博弈的双方中一方为 A，另一方为 B。然后为其中的一方 (例如 A) 寻找一个最优行动方案。

为了找到当前的最优行动方案，需要对各个可能的方案所产生的后果（得分）进行比较。

为计算得分，需要根据问题的特性信息定义一个估价函数，用来估算当前博弈树端节点的得分。

当端节点的估值计算出来后，再推算出父节点的得分。

推算的方法是：

对 “或” 节点，选其子节点中一个最大的得分作为父节点的得分，这是为了使自己在可供选择的方案中选一个对自己最有利的方案；

对 “与” 节点，选其子节点中一个最小的得分作为父节点的得分，这是为了立足于最坏的情况。 

如果一个行动方案能获得较大的倒推值，则它就是当前最好的行动方案。

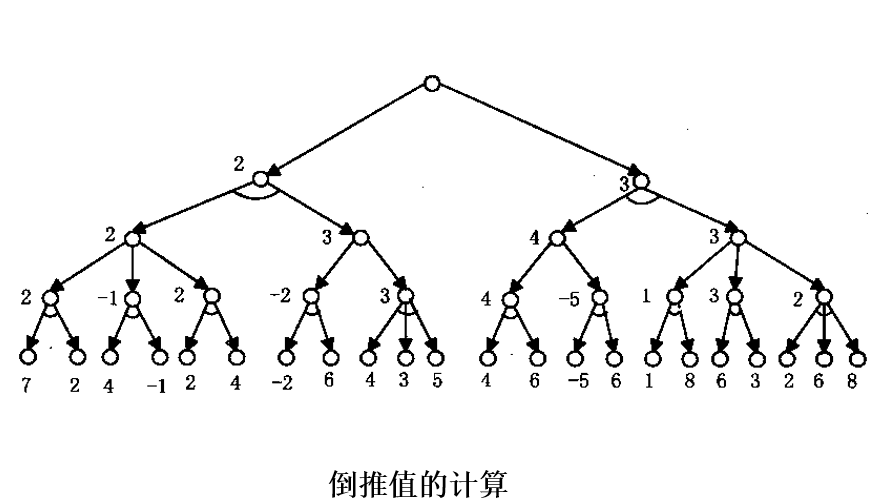
极大极小分析法：

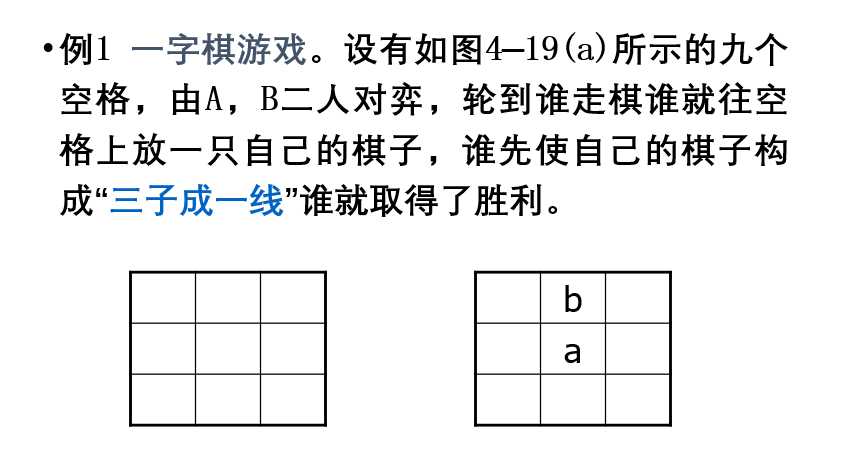
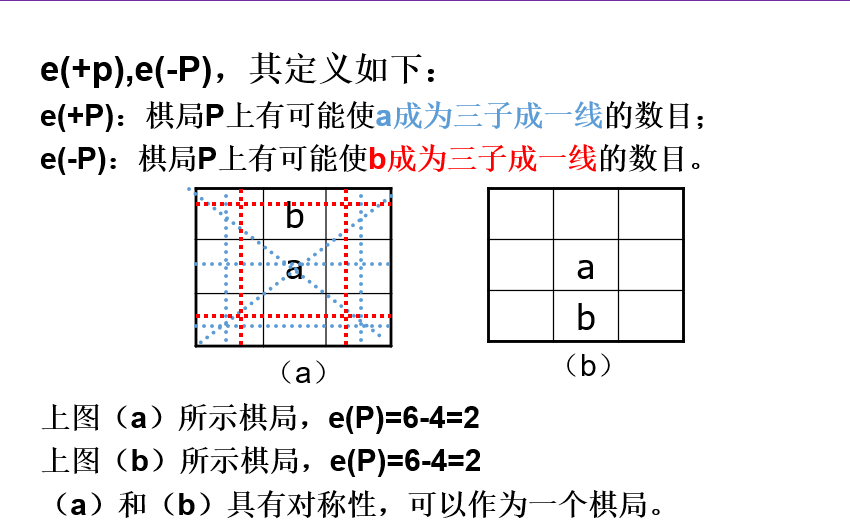
设 A 的棋子用 “a” 表示，B 的棋子用 “b” 表示。为了不致于生成太大的博弈树，假设每次仅扩展两层。估价函数定义如下：

设棋局为 P，估价函数为 e (P)。

(1) 若 P 是 A 必胜的棋局，则 e (P)=+∞。

(2) 若 P 是 B 必胜的棋局，则 e (P)=-∞。

(3) 若 P 是胜负未定的棋局，则 e (P)=e (+P)-e (-P)

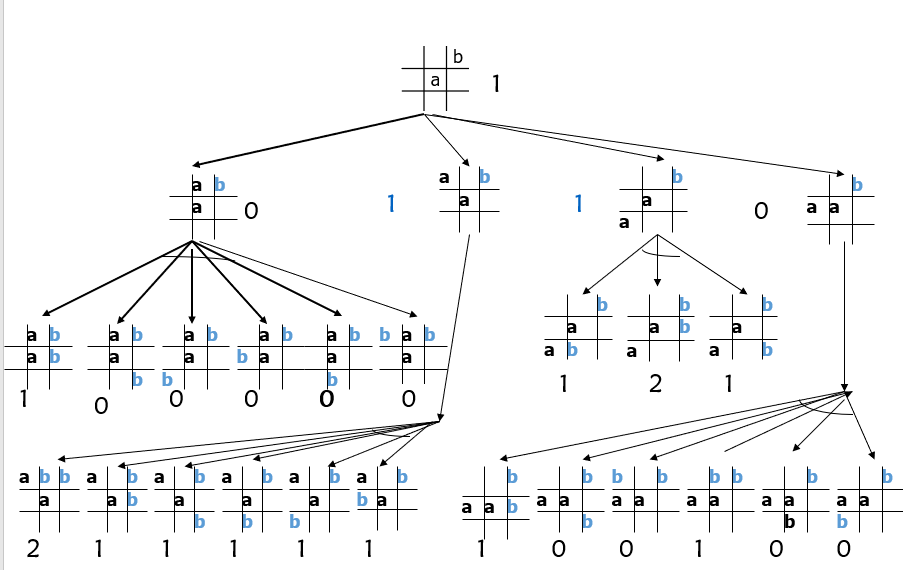
极大极小分析法的缺点是效率低。

α－ß 剪枝技术的基本思想为：

对于一个与节点 MIN, 若能估计出其倒推值的上确界 β, 并且这个 β 值不大于 MIN 的父节点 (一定是或节点) 的估计倒推值的下确界 α, 即 α≥β, 则就不必再扩展该 MIN 节点的其余子节点了 (因为这些节点的估值对 MIN 父节点的倒推值已无任何影响了)。这一过程称为 α 剪枝。

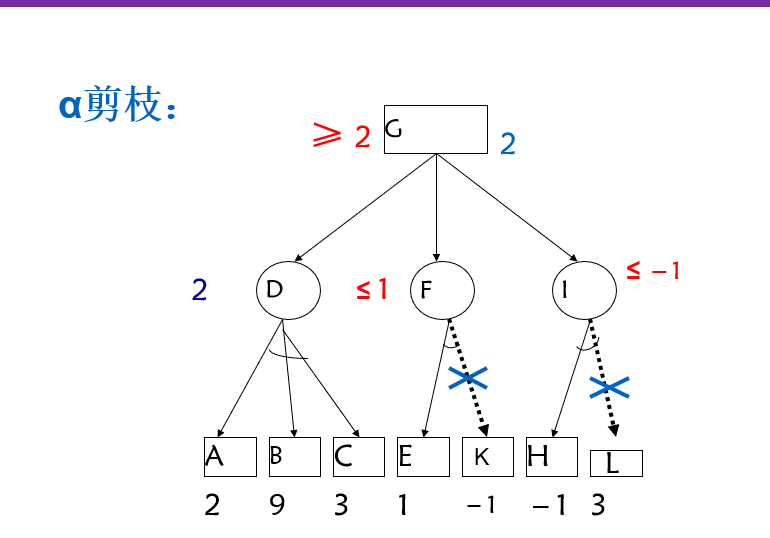
对于一个或节点 MAX, 若能估计出其倒推值的下确界 α, 并且这个 α 值不小于 MAX 的父节点 (一定是与节点) 的估计倒推值的上确界 β, 即 α≥β, 则就不必再扩展该 MAX 节点的其余子节点了 (因为这些节点的估值对 MAX 父节点的倒推值已无任何影响了)。这一过程称为 β 剪枝。

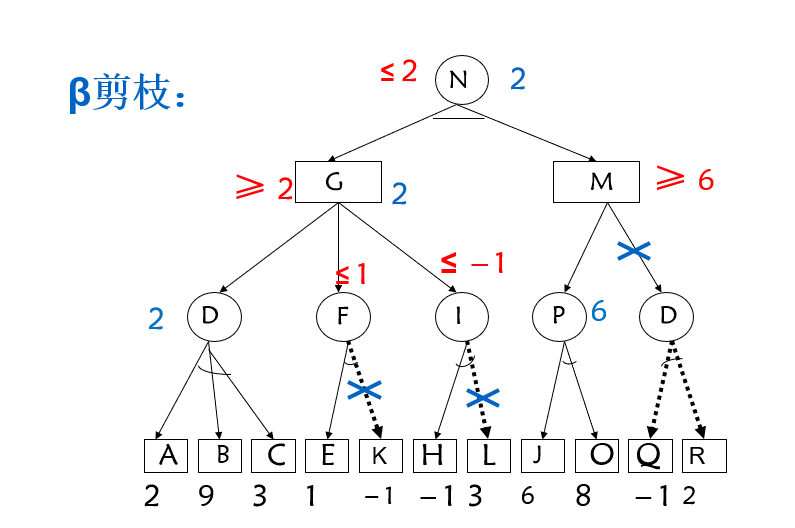
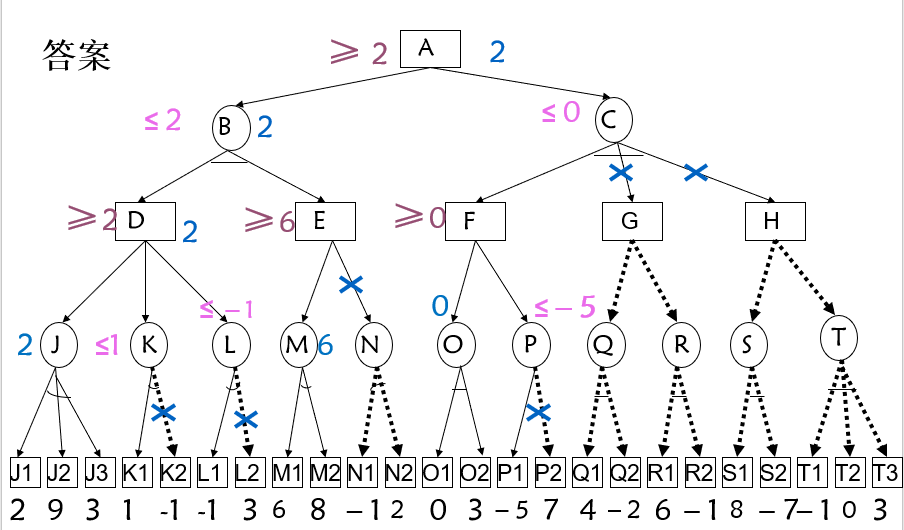
例：

 智能计算#

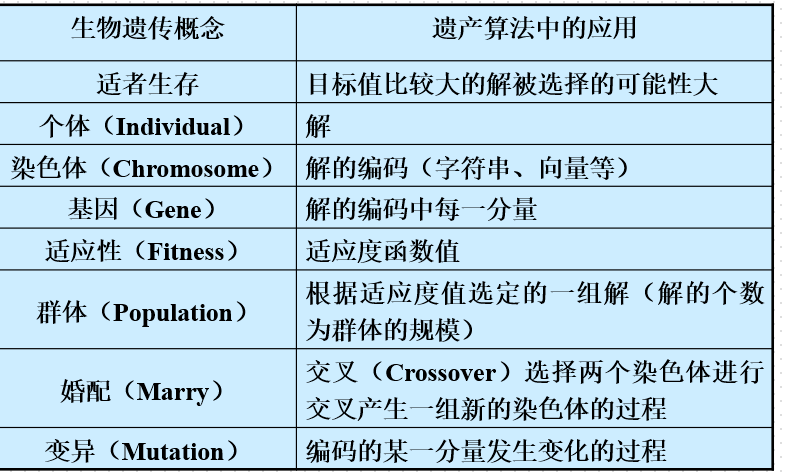
 掌握遗传算法的基本机理和求解步骤；#

基本思想

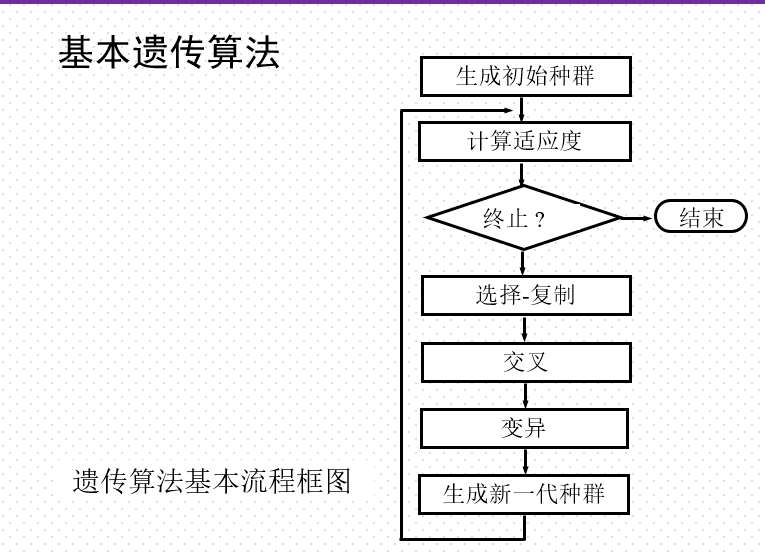
适应度函数：

尺寸变化：

在遗传算法中，将所有妨碍适应度值高的个体产生，从而影响遗传算法正常工作的问题统称为欺骗问题（deceptive problem）。 

过早收敛：缩小这些个体的适应度，以降低这些超级个体的竞争力。

停滞现象：改变原始适应值的比例关系，以提高个体之间的竞争力。

适应度函数的尺度变换（fitness scaling）或者定标：对适应度函数值域的某种映射变换。

 掌握选择 - 复制、交叉、变异三种遗传操作的设计方法；#

个体选择概率分配方法

选择操作也称为复制（reproduction）操作：从当前群体中按照一定概率选出优良的个体，使它们有机会作为父代繁殖下一代子孙。

判断个体优良与否的准则是各个个体的适应度值：个体适应度越高，其被选择的机会就越多。

个体选择概率分配方法

 了解遗传算法的应用；#

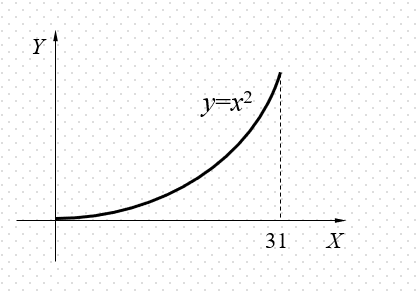
利用遗传算法求解区间［0,31］上的二次函数 y=x2 的最大值。　　

分析 

原问题可转化为在区间［0, 31］中搜索能使 y 取最大值的点 a 的问题。那么，［0, 31］ 中的点 x 就是个体， 函数值 f (x) 恰好就可以作为 x 的适应度，区间［0, 31］就是一个 (解) 空间 。这样， 只要能给出个体 x 的适当染色体编码， 该问题就可以用遗传算法来解决。

　解

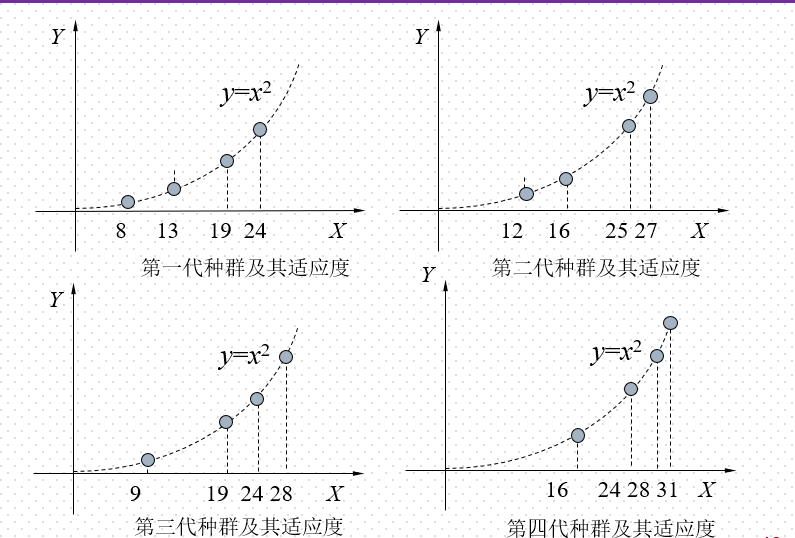
　　(1) 设定种群规模，编码染色体，产生初始种群。

将种群规模设定为 4；用 5 位二进制数编码染色体；取下列个体组成初始种群 S1:

        s1= 13 (01101),  s2= 24 (11000)

        s3= 8 (01000),    s4= 19 (10011) 

(2) 定义适应度函数。

  取适应度函数：f (x)=x^2

  　　(3) 计算各代种群中的各个体的适应度， 并对其染色体进行遗传操作，直到适应度最高的个体 (即 31（11111）) 出现为止。

首先计算种群 S1 中各个体

s1= 13(01101),    s2= 24(11000)                      

  s3= 8(01000),     s4= 19(10011)

的适应度 f (si) 。

容易求得

再计算种群 S1 中各个体的选择概率。

选择概率的计算公式为

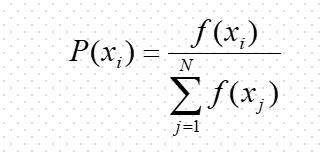
由此可求得

                          P(s1) = P(13) = 0.14

          P(s2) = P(24) = 0.49 

          P(s3) = P(8) = 0.06

          P(s4) = P(19) = 0.31   

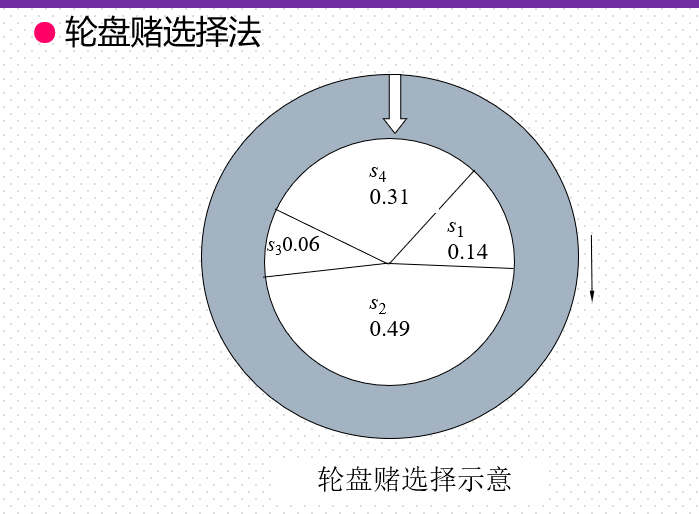
　　在算法中赌轮选择法可用下面的子过程来模拟:  　① 在［0, 1］区间内产生一个均匀分布的随机数 r。

② 若 r≤q1, 则染色体 x1 被选中。

③ 若 qk-1<r≤qk (2≤k≤N), 则染色体 xk 被选中。 其中的 qi 称为染色体 xi (i=1,  2,  …,  n) 的累积概率， 其计算公式为 

于是，得第四代种群 S4： 

s1=11111（31）,  s2=11100（28）

s3=11000（24）,  s4=10000（16） 

　  显然，在这一代种群中已经出现了适应度最高的染色体 s1=11111。于是，遗传操作终止，将染色体 “11111” 作为最终结果输出。

　　然后，将染色体 “11111” 解码为表现型，即得所求的最优解：31。

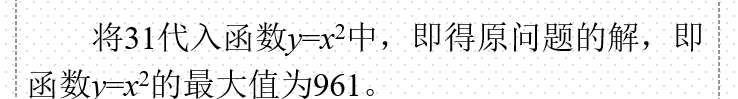
 了解粒子群优化算法#

粒子群算法的目标是使所有粒子在多维超体（multi-dimensional hyper-volume）中找到最优解。首先给空间中的所有粒子分配初始随机位置和初始随机速度。然后根据每个粒子的速度、问题空间中已知的最优全局位置和粒子已知的最优位置依次推进每个粒子的位置。随着计算的推移，通过探索和利用搜索空间中已知的有利位置，粒子围绕一个或多个最优点聚集或聚合。该算法设计玄妙之处在于它保留了最优全局位置和粒子已知的最优位置两个信息。后续的实验发现，保留这两个信息对于较快收敛速度以及避免过早陷入局部最优解都具有较好的效果。这也奠定了后续粒子群算法改进方向的基础。

基本思想

将每个个体看作 n 维搜索空间中一个没有体积质量的粒子，在搜索空间中以一定的速度飞行，该速度决定粒子飞行的方向和距离。所有粒子还有一个由被优化的函数决定的适应值。

基本原理

PSO 初始化为一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个 “极值” 来更新自己。第一个就是粒子本身所找到的最优解，这个解称为个体极值。另一个是整个种群目前找到的最优解，这个解称为全局极值。

 专家系统#

初创期

DENDRAL 系统（1968 年，斯坦福大学费根鲍姆等人）—— 推 

断化学分子结构的专家系统

MYCSYMA 系统（1971 年，麻省理工学院 ）—— 用于数学运

算的数学专家系统 

特点：高度的专业化。

专门问题求解能力强。

结构、功能不完整。

移植性差。

缺乏解释功能。

成熟期

MYCIN 系统（斯坦福大学 ）—— 血液感染病诊断专家系统 

PROSPECTOR 系统（斯坦福研究所 ）—— 探矿专家系统

CASNET 系统（拉特格尔大学）：用于青光眼诊断与治疗。

AM 系统（ 1981 年，斯坦福大学）：模拟人类进行概括、抽象和归纳推理，发现某些数论的概念和定理。

HEARSAY 系统（卡内基－梅隆大学）—— 语音识别专家系统

特点： 

（1）单学科专业型专家系统。

（2）系统结构完整，功能较全面，移植性好。

（3）具有推理解释功能，透明性好。

（4）采用启发式推理、不精确推理。

（5）用产生式规则、框架、语义网络表达知识。

（6）用限定性英语进行人－机交互。

发展期

专家系统 XCON（DEC 公司、卡内基－梅隆大学 ）：为 VAX 计算机系统制订硬件配置方案。

专家系统开发工具：

骨架系统：EMYCIN、KAS、EXPERT 等。

通用型知识表达语言： OPS5 等。

专家系统开发环境： AGE 等。

机器学习：机器学习（Machine learning）使计算机能模拟人的学习行为，自动地通过学习来获取知识和技能，不断改善性能，实现自我完善。

框架是一种 结构化的知识表示方法

编译原理中的文法属于生产式

假设我们定义了以下谓词：

Study (x)     x 肯学习

Lucky (x)     x 是幸运的

那么下列哪个谓词公式对于以下知识的表示是正确的？

"张不肯学习但他是幸运的"

﹁Study(zhang)∧Lucky(zhang)

如果定义谓词 like (x,y) 表示某一个人 x 喜欢运动项目 y，那么以下谓词公式分别表示什么意思？

本作品采用《CC 协议》，转载必须注明作者和本文链接