分类算法-支持向量机 SVM
SVM(Support Vector Machine) 指的是支持向量机,是常见的一种判别方法。在机器学习领域,是一个有监督的学习模型,通常用来进行模式识别、分类及回归分析。与其他算法相比,支持向量机在学习复杂的非线性方程时提供了一种更为清晰、更加强大的方式。
0x00线行方程组和非线性方程组的区别
线性方程组:线性方程组是各个方程关于未知量均为一次的方程组(例如2元1次方程组)。
非线性方程:非线性方程,就是因变量与自变量之间的关系不是线性的关系。
线性方程组:克莱姆法则.用克莱姆法则求解方程组 有两个前提,一是方程的个数要等于未知量的个数,二是系数矩阵的行列式要不等于零。
用克莱姆法则求解方程组实际上相当于用逆矩阵的方法求解线性方程组,它建立线性方程组的解与其系数和常数间的关系,但由于求解时要计算n+1个n阶行列式,其工作量常常很大,所以克莱姆法则常用于理论证明,很少用于具体求解。
矩阵消元法.将线性方程组的增广矩阵通过行的初等变换化为行简化阶梯形矩阵 ,则以行简化阶梯形矩阵为增广矩阵的线性方程组与原方程组同解。当方程组有解时,将其中单位列向量对应的未知量取为非自由未知量,其余的未知量取为自由未知量,即可找出线性方程组的解。
非线性方程:
非线性代数方程又称为多项式方程。令某多项式等于零可得一个多项式方程,
利用勘根法可以找出某个代数方程的解。
0x01支持向量机基础知识
-
线性可分
如下图,数据见分隔得足以分开,很容易在图中画出一条直线将数据分开,这组数据被称为线行可分数据。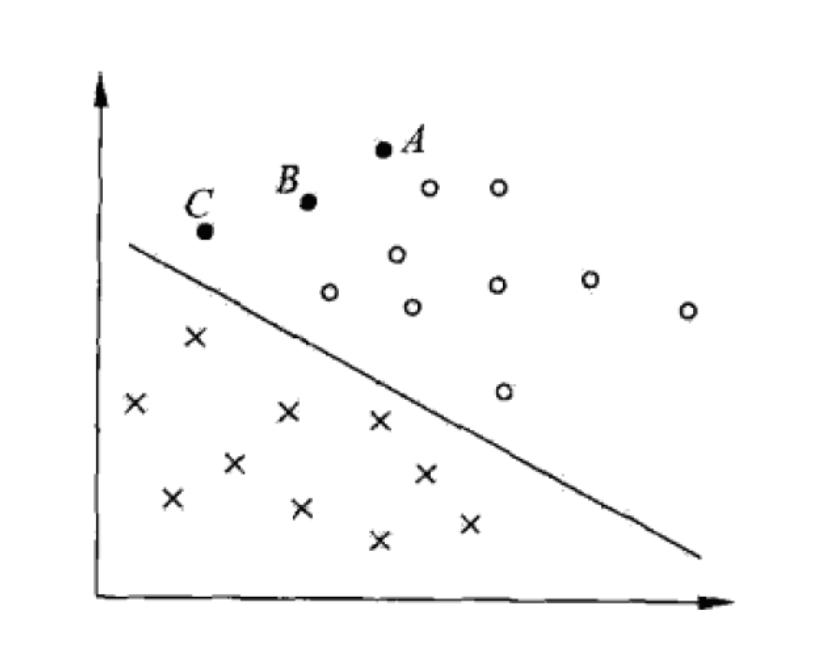
-
分隔超平面
如上图,上述将数据集分隔开来得直线成为分隔超平面,由于上面给出得数据都在二维平面上,因此此时分隔超平面就是一条直线。如果给出得数据集点是三维的,那么用来分隔数据的就是一个平面。因此更高维的情况可以以此类推,如果数据是n维的,那么就需要一个n-1维的对象来对数据进行分隔,这些统称为超平面。。 -
间隔
如下图所示,下面三个图中的都可以将数据分隔,但是哪种方式最好呢?我们希望数据点到分隔超平面的距离尽可能地远。在这里点到分割面地距离被称为间隔。间隔尽可能大是因为如果犯错或者在有限数据上训练分类器,我们希望分类器尽可能健壮。 -
支持向量
离分隔超平面最近的那些点是支持向量
分隔超平面的形式可以写成 
超平面在二维空间里就是直线,方程是ax+by+c=0超平面在三维空间里就是平面,方程是ax+by+cz+d=0 在n维空间里推广就是就是ax+by+cz+........+k=0这里的(a,b,c...)就是向量w,是由平面确定的数,(x,y,z..)是平面上任一点的坐标,就是你方程里的x,也是一个向量。
其中 w = (w1,w2,w3...wd)为法向量,决定了超平面的方向,其中d等于数据的维度,
这很好理解,假设二维的(x1,x2)点可以被 ax+b=0 分隔,这里面直线 ax+b=0 是一维的,但是这里面a和x都是二维的
b为位移项,决定了超平面与原点之间的距离
0x02最大支持向量到间隔的距离
参考资料:https://zhuanlan.zhihu.com/p/61959821
对于图中A点到分隔直线的距离为 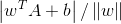
距离的理解:
上述计算结果也就是:
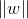 表示向量的模,
表示向量的模, ,w与w共轭的内积再开方
,w与w共轭的内积再开方
向量的内积和外积区别
向量的内积(点乘/数量积)。对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,向量内积是一个向量在另一个向量上的投影长度乘以另一个向量的长度,,如下所示,对于向量a和向量b:
![分类算法-支持向量机]
(https://cdn.learnku.com/uploads/images/202...)
a和b的点积公式为:
向量的外积(叉乘)
概括地说,两个向量的外积,又叫叉乘、叉积向量积,其运算结果是一个向量而不是一个标量。并且两个向量的外积与这两个向量组成的坐标平面垂直。定义:向量a与b的外积a×b是一个向量,其长度等于|a×b| = |a||b|sin∠(a,b),其方向正交于a与b。并且,(a,b,a×b)构成右手系。
计算方法
向量外积的性质
a × b = -b × a. (反称性)
(λa + μb) × c = λ(a ×c) + μ(b ×c). (线性)
向量外积的几何意义
在三维几何中,向量a和向量b的外积结果是一个向量,有个更通俗易懂的叫法是法向量,该向量垂直于a和b向量构成的平面。
在3D图像学中,外积的概念非常有用,可以通过两个向量的外积,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
找到支持向量后我们需要对该间隔最大化,公式:
这里的常数C用于控制最大化间隔和保证大部分点的函数间隔小于1.0这两两个目标的权重。因为所有的数据都可能有干扰数据,所以通过引入所谓的松弛变量,允许有些数据点可以处于分隔面错误的一侧。
根据上式可知,只要求出所有的a(阿尔法),那么分隔超平面就可以通过这些a(阿尔法)来表达,SVM的主要工作就是求解a(阿尔法)。
本作品采用《CC 协议》,转载必须注明作者和本文链接


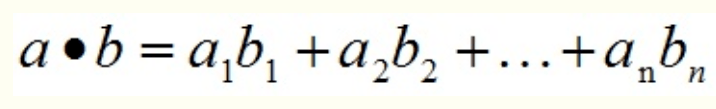
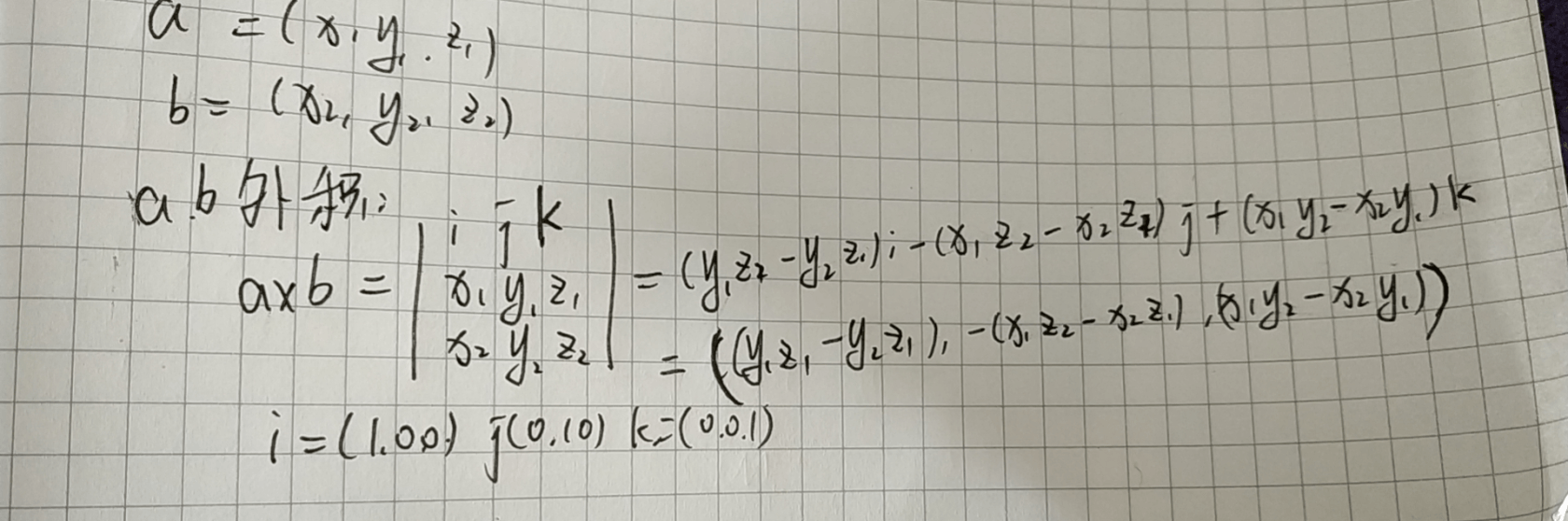



 关于 LearnKu
关于 LearnKu



