分类算法-k 邻近算法

k- 近邻 (k-NearestNeighbor，kNN) 分类算法是数据挖掘分类技术中最简单的方法之一。K- 近邻算法是通过测量不同特征值之间的距离进行分类的。基本思路是：如果一个样本在特征空间中的k 个最邻近样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在决定类别上只依据最近的一个或几个样本的类别来决定待分类样本所属的类别。KNN 算法中，所选择的邻居都是已经正确分类的对象。该方法在分类决策上只依据最邻近的一个或几个样本的类别来决定待分类样本所属的类别。

0x00欧式距离和马氏距离

欧式距离计算公式：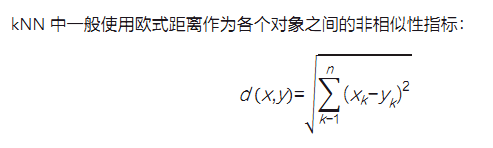

当然也可以使用马氏距离 Mahalanobis distance 等测显距离的方法。在K近够算法中，当训练集通近邻值k、距离度量、决策规则等确定下来时，整个算法实际上是利用训练集把特征空间划分成一个个子空间，训练集中的每个样本占据部分空间。 对最近邻而言，当测试祥本落在莫个训练样本的领域内，就把测试样本标记为这一类。

马氏距离是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。 对于一个均值为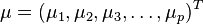，协方差矩阵为Σ的多变量矢量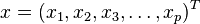，其马氏距离为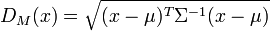

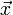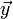马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度：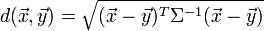

如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离；如果协方差矩阵为对角阵，其也可称为正规化的马氏距离。

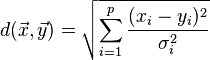
其中σi是xi的标准差。

对于上述的马氏距离，本人研究了一下，虽然看上去公式很简单的，但是其中存在很多模糊的东西，为什么马氏距离是一种考滤到各种特性之间的联系并且是尺度无关的？为什么可以使用协方差矩阵的逆矩阵去掉单位而使之尺度无关。基于此，以下是个人的一些想法。

0x01k-近邻算法的一般流程如下。

①计算测试数据与各个训练数据之间的距离。

②按照距离的递增关系进行排序。

③选取距离最小的k个点。

④确定前k个点所在类别的出现频率。

⑤返回前k个点中出现频率最高的类别作为测试数据的预测分类。

统计学习方法中参数选择-般是要在偏差(Bias)与方差(Variance)之间取得一个平衡(Tradeoff)。对kNN而言，k值的选择也要在偏差与方差之间取得平衡。若k取值很小，如k=1,则分类结果容易因为噪声点的干扰而出现错误，此时方差较大;若k取值很大，如k=N(N为训练集的样本数)，则对所有测试样本而言，结果都-一样， 分类的结果都是样本最多的类别，这样稳定是稳定了，但预测结果与真实值相差太远，偏差过大。 因此，k值既不能取太大也不能取太小，通常的做法是，利用交叉验证(Cross Vldation)评估- -系列不同的k值，选取结果最好的k值作为训练参数。

本作品采用《CC 协议》，转载必须注明作者和本文链接