「Neural Factorization Machines for Sparse Predictive Analytics」- 论文摘要

1、前言#

FM 能够有效的发现二阶组合特征，但存在的问题在于，FM 捕获的二阶组合特征是线性组合的（其表达式就是线性组合），无法捕获非线性组合特征。现在深度神经网络可以发现非线性的组合特征，例如谷歌的 Wide&Deep，微软的 DeepCross，但对于这些深度网络，存在的缺点是很难训练。本文提出 NFM 模型，其能将 FM 模型捕获的二阶线性组合特征以及神经网络捕获的高阶非线性组合特征组合起来。NFM 比 FM 更具表现力，因为 FM 可以被看作是 NFM 不含隐藏层的特例。

2、Introduction#

组合特征 (cross feature)，例如 occupation = {banker,doctor}， дender = {M,F} 则其组合特征为 occupation_ender = {banker_M,banker_F,doctor_M,doctor_F}。
FM 能够很好的捕获二阶组合特征，但其缺点是它毕竟还是属于线性模型，它的表达能力受限，而且它只能对二阶组合特征进行建模。

NFM 针对 FM 的缺点，在二阶特征组合的隐向量空间中，引入了非线性变换来提升模型非线性表达能力；同时，也可以学习到高阶的组合特征。

3、MODELLING FEATURE INTERACTIONS#

最近几年，embedding-based 方法越来越受欢迎，通过把高维稀疏的输入 embed 到低维度的稠密的隐向量空间中，模型可以学习到训练集中没有出现过的特征组合。大致分为两类：

factorization machine-based linear models
neural network-based non-linear models

3.1、FM
公式：

$\hat{y} {FM} (x) =w_0 + \sum ^n _{i=1} w_ix_i + \sum^n _{i=1} \sum^n{j=i+1} v^Tv_j \cdot x_i x_j$

FM 很好的解决了高纬度高稀疏输入特征组合的问题。通过隐向量内积来建模权重，针对在训练集中没有出现过的特征组合或者出现次数很好的特征组合，也能有效的学习。
参数：

$\theta \in \left \{ w_0, \{ w_i\},\{ v_{if}\} \right \}$

，表达式可写作：y (x) = g + hθ

3.2、DNN#

业内大部分 DNN 的架构都是：把特征的嵌入向量简单拼接起来，输入到神经网络中学习。这样简单的拼接嵌入向量，因为缺失了很多组合特征的信息效果并不好，那么只能寄希望于后面的 MLP 可以弥补不足。但是为了提高 NN 的学习能力就需要增加网络层数，复杂的网络结构会收到诸如梯度消失 / 爆炸、过拟合、degradation (随着网络层数的增加，训练准确率不升反降，非常反常) 等问题的困扰，网络的学习或者优化会非常困难。

如果不对嵌入层预训练，Wide&Deep 和 DeepCross 的性能比 FM 还差，而且 DeepCross 严重过拟合，Wide&Deep 遇到了 degradation 问题。
如果使用 FM 预训练初始化嵌入层，Wide&Deep 和 DeepCross 性能都提升了，甚至超过了 FM。Wide&Deep 的 degradation 问题也解决了，因为训练集的性能得到了提升。但是两者依旧都有过拟合的问题。实验说明 DNN 的训练学习真的存在困难。

NFM 丢弃了直接把 embedding vector 拼接输入到神经网络的做法，而是采用在 embedding 层后增加了 Bi-Interaction 操作来对二阶组合特征进行建模。这使得 low level 的输入表达的信息更加的丰富，极大的提高了后面隐藏层学习高阶非线性组合特征的能力。

4、Neural Factorization Machines#

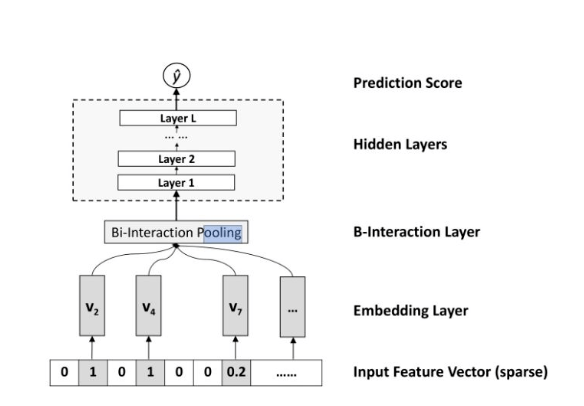
结构图：

公式：

$\hat{y}_{NFM}(x) = w_0 + \sum^n _{i=1}w_ix_i +f(x)$

其中 f (x) 是 NFM 的核心，用来学习二阶组合特征和高阶的组合特征模式。前面两项为线性回归部分，与 FM 相似。

4.1、Embedding Layer#

Embedding 将输入转换到低维度的稠密的嵌入空间中进行处理。然后与原始特征进行相乘得到 Embedding vector，Vx = {x1v1,…,xnvn}，而不是简简单单的使用 embedding_lookup。

4.2、Bi-Interaction Layer#

把 embedding vector 喂给 Bi-Interaction Layer，采用了类似 pooling 操作，把多个向量转换成一个向量，形式化如下：

$f_{BI}(V_x) = \sum^n_{i=1}\sum^n_{j=i+1} x_iv_i\bigodot x_jv_j$

对公式的理解：fBI 的输入是整个的 embedding 向量，xi xj 是特征取值，vi vj 是特征对应的 embedding 向量。中间的操作表示对应位置相乘。所以原始的 embedding 向量任意两个都进行组合，对应位置相乘结果得到一个新向量；然后把这些新向量相加，就得到了 Bi-Interaction 的输出。这个输出只有一个向量。上式可参考 FM 的优化方法得到：

$f_{BI}(V_x) =\frac{1}{2} \begin{bmatrix} (\sum^n_{i=1} x_i v_i )^2 - \sum^n _{i=1}(x_i v_i)^2 \end{bmatrix}$

它的计算复杂度是 O (NK)，其中 k 是嵌入向量的维度，N 是输入 x 中非零特征的个数。

Bi-Interaction Layer 实现了对二阶组合特征的建模，但是又没有引入额外的开销，包括参数数量和计算复杂度。

4.3、Hidden Layers#

表达式：

$\begin{matrix} z_1= \sigma (W_1 f_{BI}(V_x) + b_1),\\ z_2=\sigma (W_2 z_1 + b_1) \\ ...\\ z_L=\sigma (W_L z_{L-1} + b_L) \end{matrix}$

其中 Zi 表示的是隐藏层，以此来学习高阶组合特征。
隐藏层结构图类型（每个隐藏层大小）有 tower，constant，diamond 等，一般选用 constant 的效果要好一些。本文实验中 NFM 使用一个隐藏层得到了最好的效果。

4.4、Prediction Layer#

最后一层隐藏层 zL 到输出层最后预测结果公式如下：

$f(x) = h^Tz_L$

其中 h 是中间的网络参数。

综上 NFM 的表达式总结如下：

$\hat y_{NFM}(x) = w_0 + \sum^n_{i=1} w_ix_i +h^T\sigma_L(w_L(…\sigma(w_1F_{BI}(V_x)+b_1…) +b_L$

参数：

$\Theta = \{w_0, \{ w_i, v_i \}, h, \{ w_l, b_l\}\}$

对比 FM，NFM 模型的参数主要是 {Wl,bl}，这个是学习高阶组合特征的参数。相比于 FM 其实多出的参数就是隐藏层的参数。FM 也可以看做是一个神经网络架构，就是去掉隐藏层的 NFM。我们把去掉隐藏层的 NFM 称为 NFM-0，形式化如下：

$\begin{matrix} \displaystyle \hat y_{NFM-0} = w_0 + \sum^n _{i=1} w_ix_i +h^T \sum^n_{i=1}\sum^n_{j=i+1}x_iv_i\bigodot x_j v_j\\ = w_0 +\sum^n _{i=1}w_ix_i + \sum^n_{i=1} \sum^n_{j=i+1} \sum^k_{f=1}h_{fv_{if}v_{if}\cdot x_ix_j} \end{matrix}$

如果 h 为全 1 向量，那么此时 NFM 就是 FM。

这是第一次把 FM 看做是神经网络来处理，这样的观点对于优化 FM 提供了一些新的思路。同时，像 NN 中常用的技巧也可以应用到这里面来，比如 Dropout，实验发现在正则化 FM 的时候，使用 Dropout 比传统的 L2 正则化还要有效。

5、NFM vs Wide&Deep、DeepCross#

最重要的区别就在于 Bi-Interaction Pooling。Wide&Deep 和 DeepCross 都是用拼接操作 (concatenation) 替换了 Bi-Interaction，并且隐藏层运用 tower 结构的 MLP（或残差单元）。

Concatenation 操作的最大缺点就是它并没有考虑任何的特征组合信息，所以就全部依赖后面的 MLP 去学习特征组合，但是很不幸，MLP 的学习优化非常困难。
使用 Bi-Interaction 考虑到了二阶特征组合，使得输入的表示包含更多的信息，减轻了后面 MLP 部分的学习压力，所以可以用更简单的模型，取得更好的成绩。

6、Learning#

6.1、目标函数#

NFM 可以用于分类、回归、ranking 问题，对应着不同的目标函数。

回归：square loss
分类：Hinge Loss 或 log loss
ranking：Contrastive max-margin loss

本中以回归问题为例，使用 square loss，表达式如下：

$L_{reg} = \sum_{x\in \chi} (\hat y (x) - y(x))^2$

这里并没有正则化项，因为作者发现在 NFM 中使用 Dropout 能够得到更好的效果。

6.2、参数估计#

使用 mini-batch Adagrad 来进行参数估计，Adagrad 是 SGD 的变体，特点是每个参数都有自己的学习速率。然后让参数沿着目标函数负梯度的方向进行更新，是下降最快的方向，形式化如下：

$\theta = \theta - \eta \cdot 2(\hat y(x) - y(x))\frac{d\hat y(x)}{d\theta}$

Bi-Interaction 在求梯度的做法：

$\frac{df_{BI}\nu _X}{DV_i} = (\sum ^n _{j=1} x_jv_j)x_i - x^2_i v_i = \sum ^n _{j=1,j=1} x_ix_jv_j$

所以 NFM 的训练依旧可以是端到端的训练，只需要把 Bi-Interaction 插入到网络中即可。

6.3、Dropout#

在 NFM 中，Bi-Interaction 的输出后就增加了 Dropout 操作，随机的丢弃了一部分的输出。随后的 MLP 同样应用了 Dropout。Dropout 在 NFM 中可以有效的抑制过拟合。

6.4、Batch Normalization#

DNN 的训练面临很多问题。其中一个就是协方差偏移 (covariance shift)，意思就是：由于参数的更新，隐藏层的输入分布不断的在变化，那么模型参数就需要去学习这些变化，这减慢了模型的收敛速度。

$BN(x_i) = \gamma \bigodot (\frac{x_i - \mu _B}{\sigma _B}) + \beta$

对于隐藏层的输入，BN 在 mini-batch 数据上，把输入转换成均值为 0，方差为 1 的高斯分布。其中的 gamma、beta 是两个超参数，为了扩大模型的表达能力，如果模型发现不应用 BN 操作更好，那么就可以通过学习这两个参数来消除 BN 的影响。NFM 中 Bi-Interaction Layer 的输出就是 MLP 的第一个输出，包括后面所有隐藏层的输入都需要进行 Batch Normalization。Batch Normalization 在 NFM 中可以加快训练速度。

如果用 FM 来 pre-train 嵌入层，NFM 会收敛的非常快，但是 NFM 最终的效果并没有变好。说明 NFM 对参数有很好的鲁棒性。

7、总结#

NFM 主要特点：

引入了 Bi-Interaction Layer，采用 Pooling 操作将多个 embedding vector 转化成一个 vector
加入了 NN，用于发现高阶非线性组合特征

本作品采用《CC 协议》，转载必须注明作者和本文链接