卷积神经网络
理论
- 卷积神经网络
- 卷积操作、池化操作、全连接操作
- 深度可分离卷积
- 数据增强
- 迁移学习
卷积神经网络
「卷积神经网络」主要用于图像方向的深度学习神经网络。
结构
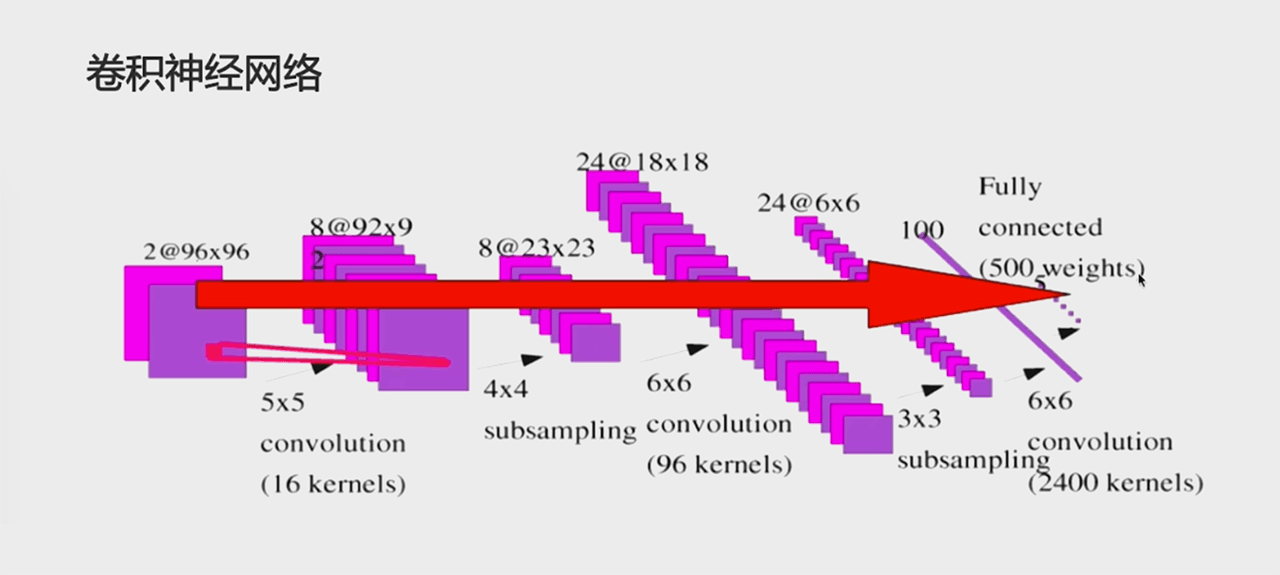
卷积神经网络:
(卷积层 + (可选)池化层) * N + 全连接层 * M
(C_{onvolutionalLayer} + (可选)S_{ubsamplingLayer})*N + D_{enseLayer} * M\\{}\\ N\geqslant1,M\geqslant0
卷积层的输入和输出都是矩阵,全连接层的输入和输出都是向量,所以最后一层卷积层后要做展平。
「卷积神经网络」适用于分类任务或回归任务,一般用于分类任务。
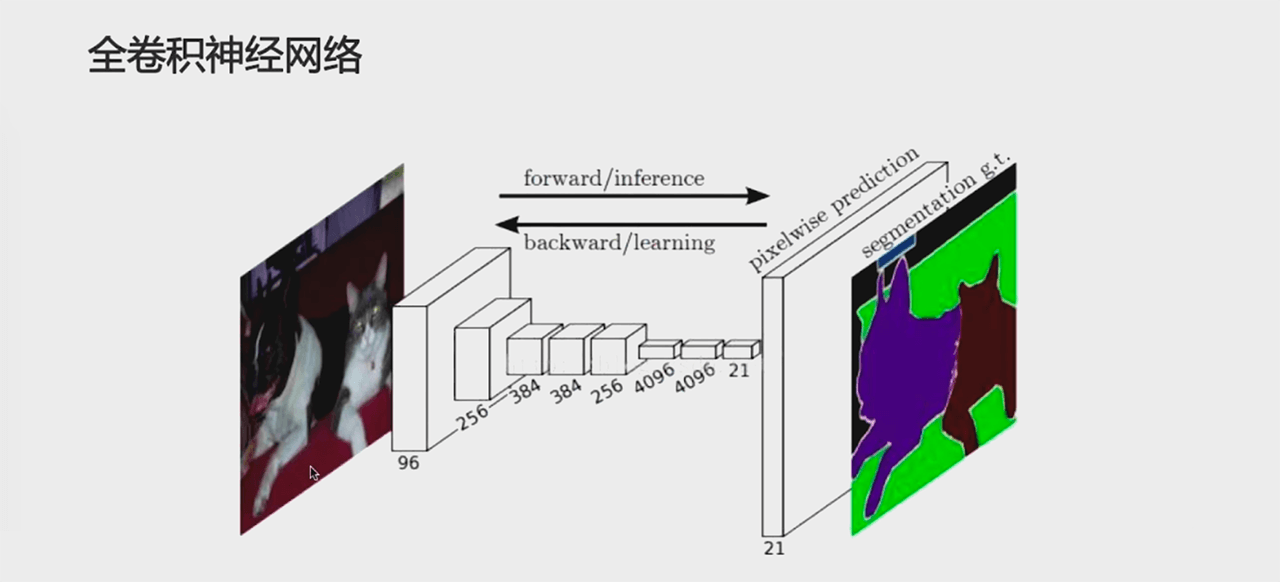
全卷积神经网络:
(卷积层 + (可选)池化层) * N + 反卷积层 * K
(C_{onvolutionalLayer} + (可选)S_{ubsamplingLayer})*N + De_{convolutionLayer} * K\\{}\\ N\geqslant1,M\geqslant0
「全卷积神经网络」适用于物体分割任务,因为输入和输出的尺寸是一样的。
卷积解决的问题
神经网络遇到的问题:
- 参数过多
- 计算资源不足
- 例:图像大小 1000*1000
- 下一层神经元为 10^6
- 全连接参数为 1000 * 1000 * 10^6=10^12
- 一层全连接层就有一万亿个参数,这是现代计算机无法承受的。
- 容易过拟合,需要更多训练数据
- 计算资源不足
解决方案之「局部连接」:
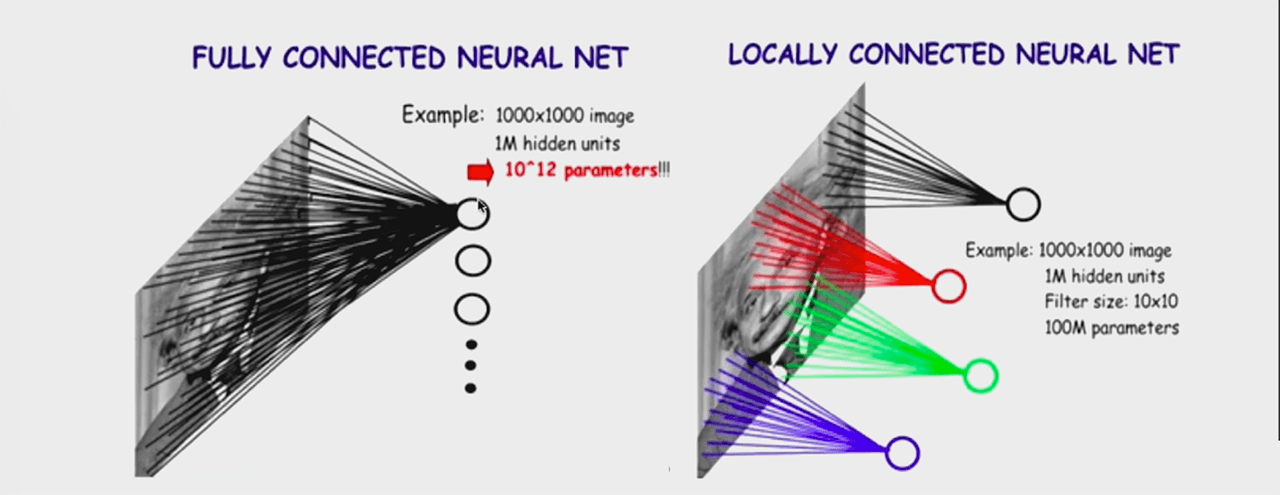
上图中,右侧是「局部连接」:
- 图像大小 1000*1000
- 下一层神经元为 10^6
- 局部连接范围为 10*10
- 全连接参数为 10 * 10 * 10^6 = 10^8
解决方案之「参数共享」:
参数共享指的是不同的局部连接之间的参数是一样的,比如上图的红色连接中有 100 个参数,蓝色连接中也有 100 个参数,这个红色连接的参数和蓝色连接的参数是同一组 100 个参数。
经过参数共享之后:
- 图像大小 1000*1000
- 下一层神经元为 10^6
- 局部连接范围为 10*10
- 全连接参数为 10 * 10 = 10^2
因为做了参数共享,所以局部范围和下一层神经元就没有关系了。
我们从 1000000000000 个参数变成了 100 个参数,为局部连接有效呢?这是图像问题本身所决定的。
对于图像问题来说,图像具备很强的区域性。比如爱因斯坦的肖像那张图中相近的像素的值很相近,对于额头、脸颊或者对于嘴部区域,相近的像素的值都很接近。对于爱因斯坦肖像图,无论构图时是把爱因斯坦的脸放在图像中间还是左上左下右上右下,仍然是一张脸。对于脸部特征来说,构图位置无论在图像中的哪里,都是脸部信息。参数共享提供了这种可能性,使得无论如何构图,都能用同一组参数进行处理,得到图像是一张脸的事实。如果不用参数共享,很有可能只能得到中间位置的脸,脸部挪到图像边上去可能就检测不出来了。
- 局部连接
- 图像的区域性
- 参数共享
- 图像特征与位置无关
小知识点补充:神经网络容量是指可以学习到的信息量。
卷积操作
卷积 —— 每个位置进行计算
输入图像:
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
卷积核:
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
输出:
| ? | ? | ? |
| ? | ? | ? |
| ? | ? | ? |
卷积核围绕输入数据滑动方向为从左往右从上往下滑动
输出size = 输入size - 卷积核size + 1
输出size = 输入size - (卷积核size - 1)
O_{size}=I_{size}-Convolutionkernel_{size}+1
左上角卷积计算「点积乘法」:
result=1\times1+1\times3+1\times7+1\times11+1\times13=35
得出输出矩阵的左上角结果:
| 35 | ? | ? |
| ? | ? | ? |
| ? | ? | ? |
第二步卷积计算「点积乘法」:
result=1\times2+1\times4+1\times8+1\times12+1\times14=40
得出输出矩阵的第二步结果:
| 35 | 40 | ? |
| ? | ? | ? |
| ? | ? | ? |
以上卷积核滑动步长默认为 1,如果步长为 2,意味着第一步卷积核对输入图像的红色部分进行计算:
1 |
2 |
3 |
4 | 5 |
6 |
7 |
8 |
9 | 10 |
11 |
12 |
13 |
14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
第一步卷积核对输入图像的红色部分进行计算:
| 1 | 2 | 3 |
4 |
5 |
| 6 | 7 | 8 |
9 |
10 |
| 11 | 12 | 13 |
14 |
15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
步长越长,输出矩阵越小,比如以上输入图像矩阵经过 3*3 卷积核计算,输出矩阵大小为 2*2:
result_{step2}=1\cdot3+1\cdot5+1\cdot9+1\cdot13+1\cdot15=45
输出:
| 35 | 45 |
| ? | ? |
步长太大会引发一个问题: 如果是一个深度卷积神经网络,每一层矩阵规格的减小,会使得图像最后消没了。 这样的问题有一个解决方法 —— 「Padding」 将输入图像矩阵外圈补 0。比如以上的输入数据补成:
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 | 2 | 3 | 4 | 5 | 0 |
0 |
6 | 7 | 8 | 9 | 10 | 0 |
0 |
11 | 12 | 13 | 14 | 15 | 0 |
0 |
16 | 17 | 18 | 19 | 20 | 0 |
0 |
21 | 22 | 23 | 24 | 25 | 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
经过卷积核计算后输出:
| ? | ? | ? | ? | ? |
| ? | ? | ? | ? | ? |
| ? | ? | ? | ? | ? |
| ? | ? | ? | ? | ? |
| ? | ? | ? | ? | ? |
这样卷积核的中间点的位活动的位置就变大了,使得输出可以变得和输入图像一样大,甚至可以变得更大,一般情况下,只需要补 0 补到一样就可以了。
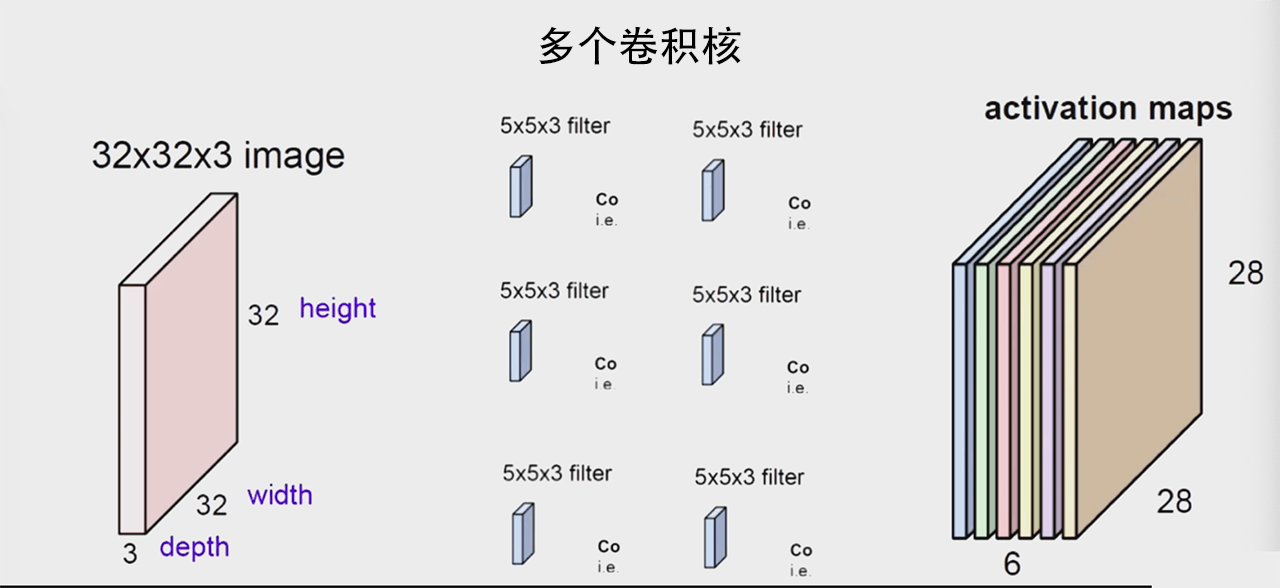
以上输入的的都单通道的,现实场景中图像是多通道的,比如 RGB 三通道,对于多通道的卷积处理方式:
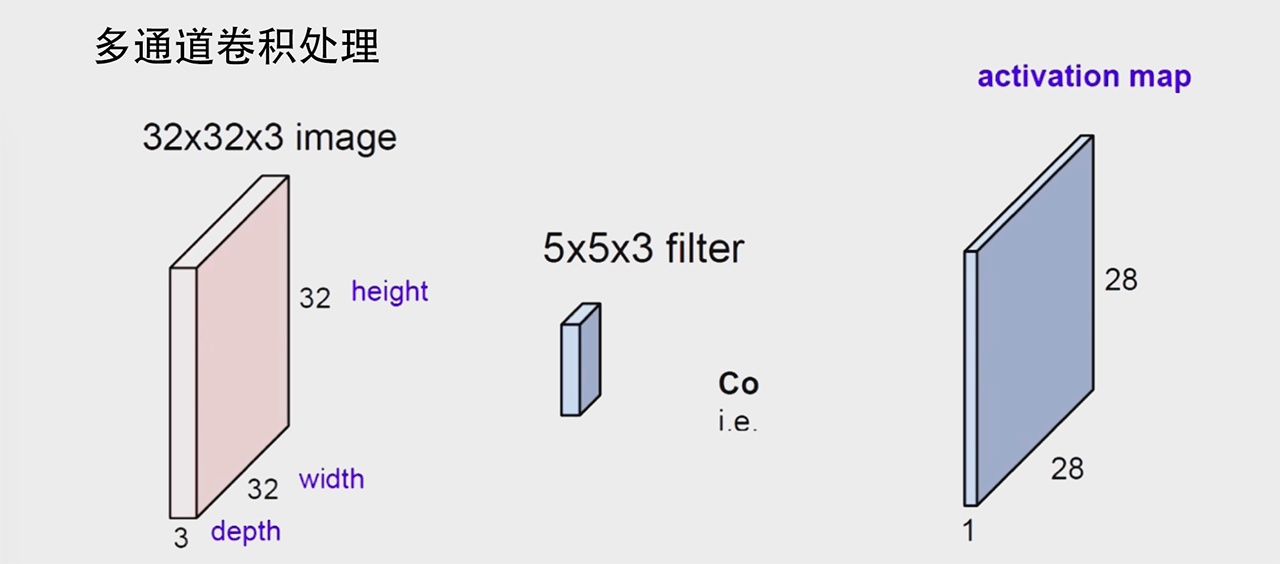
上图可以看出一个卷积核可以提取一组特征,从多通道输入变成了单通道输出,但是项目一般都需要多通道输出:
还有一种操作,输入通道数为 4,输出通道数为 2,对每个通道分别做操作,加和到输出W^1。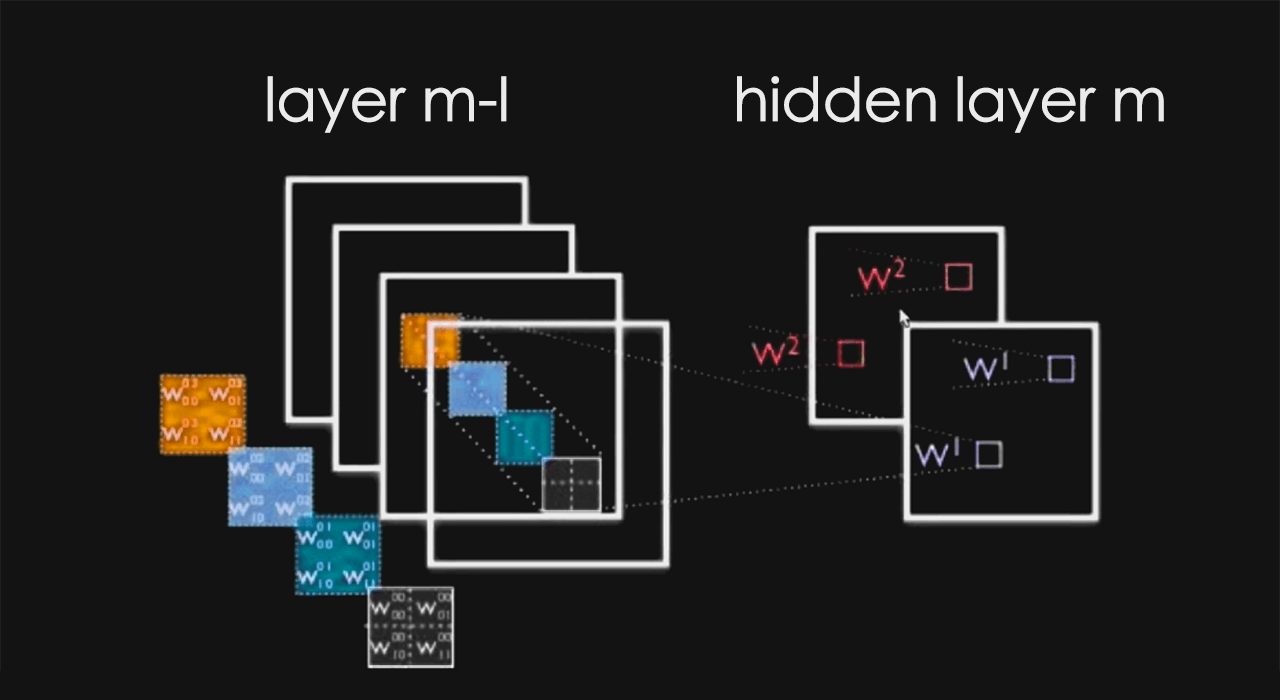
池化操作
最大值池化
输入图像
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
最大池化核:
Max-pool 操作
Stride = 2
Kernel_size = 2*2
| - | - |
| - | - |
输出:
| 7 | 9 |
| 17 | 19 |
平均池化核:
Avg-pool 操作
Stride = 2
Kernel_size = 2*2
输出:
| 4 | 6 |
| 14 | 16 |
池化操作特点:
- 常使用不重叠、不补零
- 没有用于求导的参数
- 池化层参数为步长和池化核大小
- 用于减少图像尺寸,从而减少计算量
- 一定程度平移鲁棒
- 损失了空间位置精度
本作品采用《CC 协议》,转载必须注明作者和本文链接




 关于 LearnKu
关于 LearnKu



