深度可分离卷积
模型结构
深度可分离卷积是普通卷积操作的一个变种,它可以替代不同卷积从而构成卷积神经网络。
在卷积神经网络里,把上图中左图结构替换成右图结构,就构成了深度可分离卷积神经网络。右图中 1x1 卷积就是普通卷积。
右图中 3x3 的深度可分离卷积是怎么一回事,这要从「Inception V3」模型结构说起,「Inception V3」是 Google 在 2016 年提出来的网络模型结构,这结构的思想,启发了深度可分离卷积。
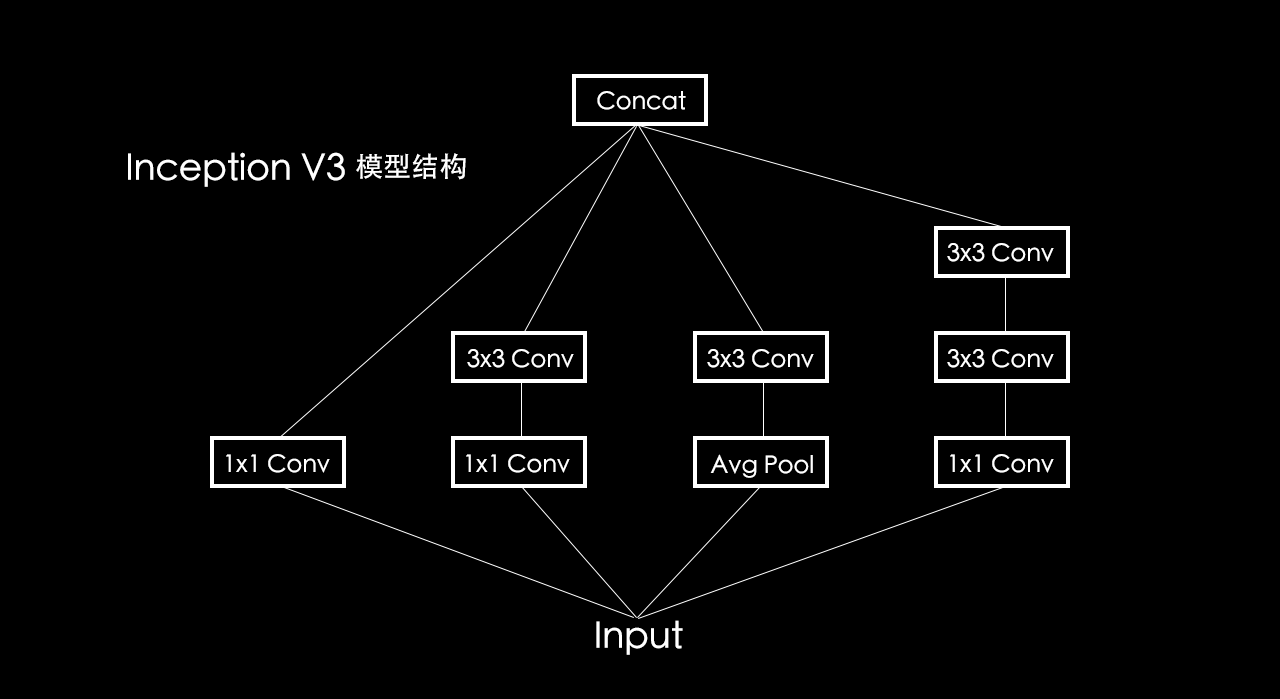
可以看到「Inception V3」模型结构中输入被分成了四个分支,最后被合并起来输入给下一个子结构。
这样做分支能得到不同尺寸「视野域」。
图同视野域提取的图像特征尺寸不同。
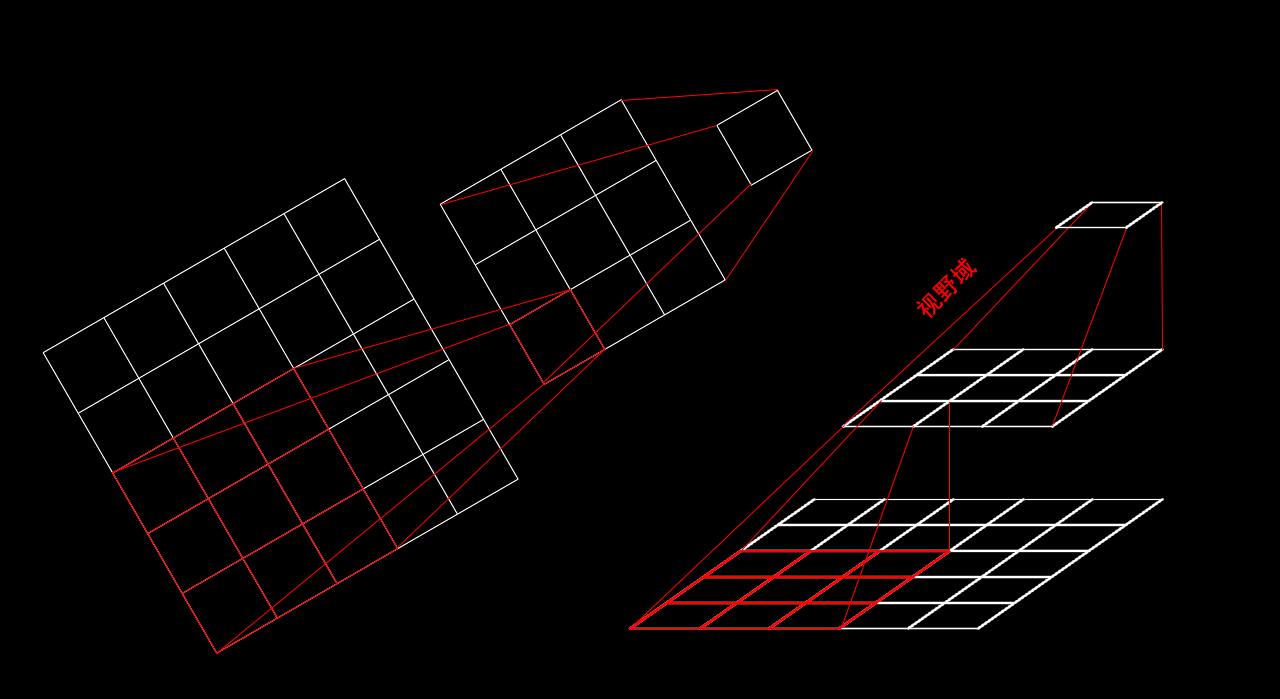
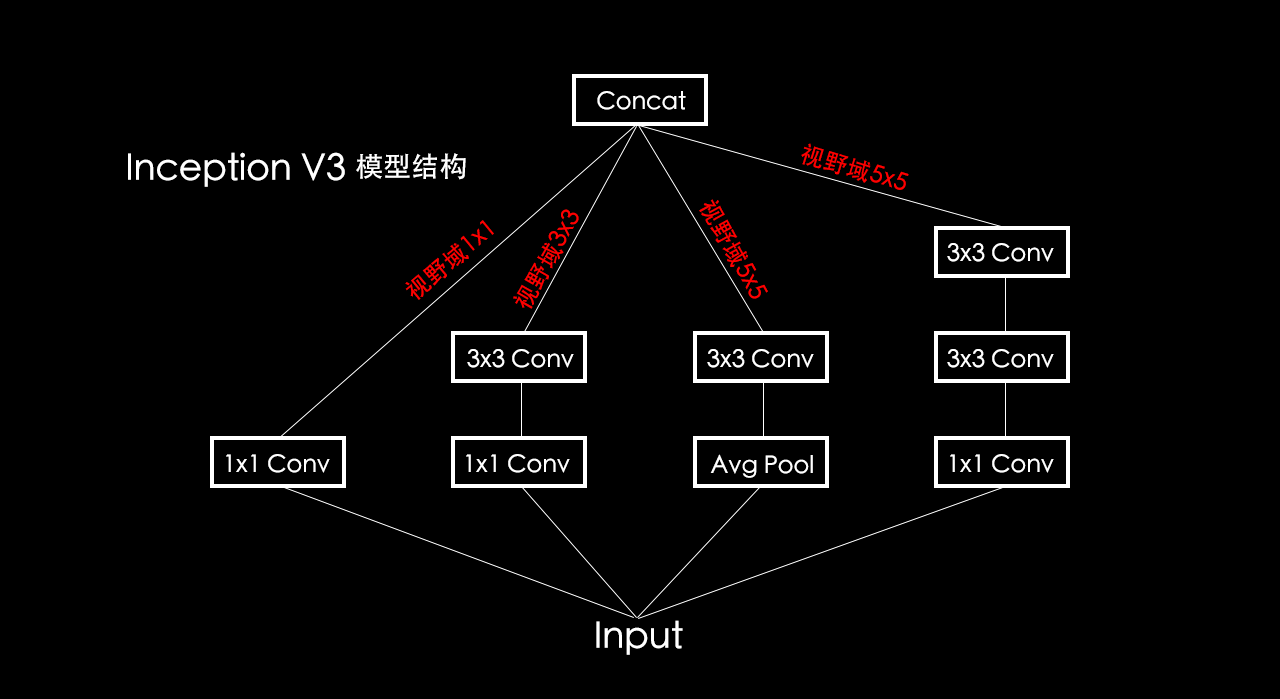
分支操作除了能得到不同的「视野域」,使数据信息更充分,相对于不做分支的模型结构还能提升效率。
深度可分离卷积模型结构
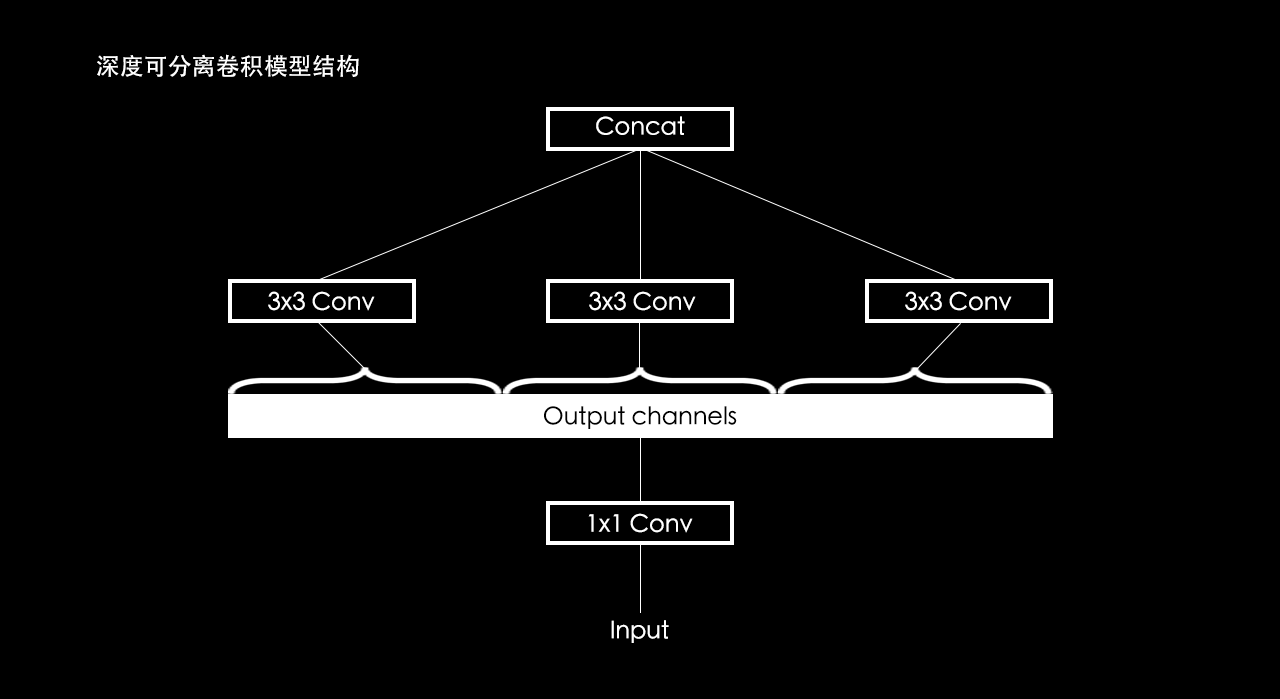
分到极致:
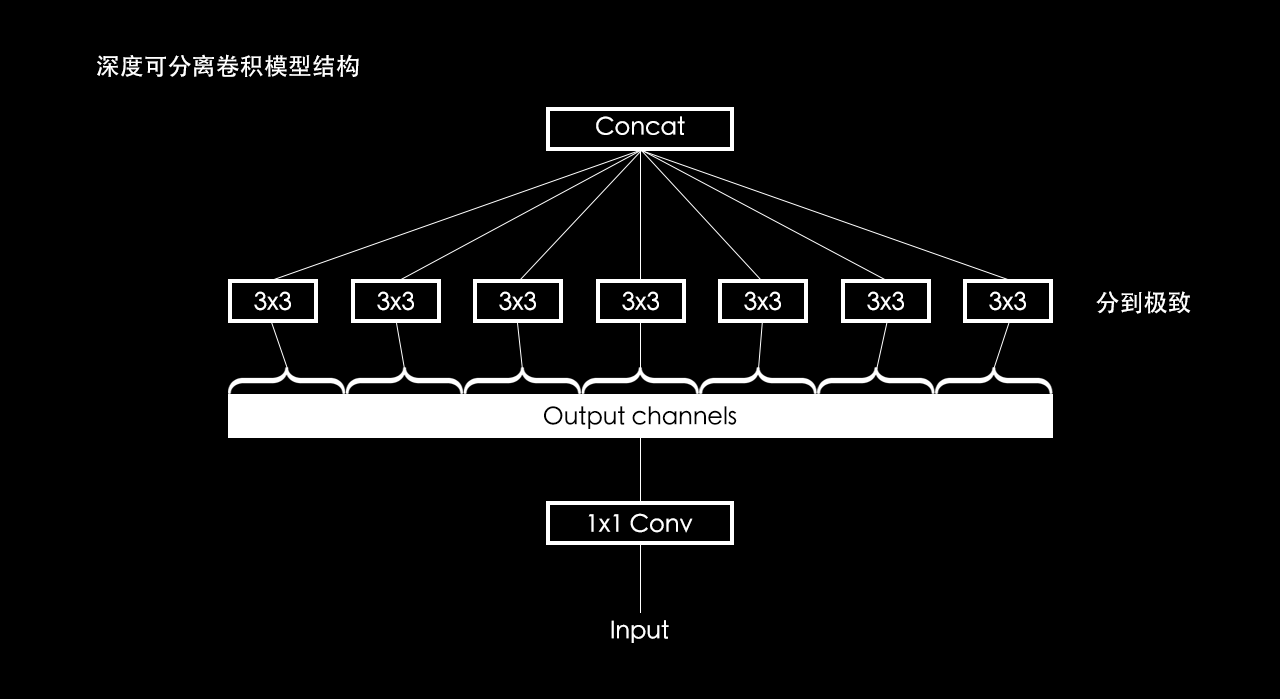

输出图像中的一个通道只和输入图像中的一个通道有关系,而不是和输入图像中的所有通道有关系。所以深度可分离卷积比起普通卷积,计算量少了很多。
普通卷积计算量:
D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F\\{}\\ D_K^2=Kernel_{size}\\{}\\ D_F^2=Input_{size}\\{}\\ M=Input_{\#channel}\\{}\\ N=Output_{\#channel}=\#Kernel
一般情况下,会把卷积核设置成正方形的,所以是D_K\cdot D_K,输入图像的大小也会设置成正方形,所以是D_F\cdot D_F。计算量公式中由于加法很简单,复杂度没有乘法高,所以忽略了加法计算。
深度可分离卷积计算量:
D_K\cdot D_K\cdot M\cdot D_F\cdot D_F\\{}\\ _{深度可分离计算量}\\{}\\ M\cdot N\cdot D_F\cdot D_F\\{}\\ _{1\times1卷积计算量}
深度可分离卷积与普通卷积的计算量加速比:
\displaystyle _{优化比例}\\{}\\ \frac{D_K\cdot D_K\cdot M\cdot D_F\cdot D_F+M\cdot N\cdot D_F\cdot D_F}{D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F}\\{}\\ =\frac{1}{N}=\frac{1}{D_K^2}
本作品采用《CC 协议》,转载必须注明作者和本文链接




 关于 LearnKu
关于 LearnKu



