基于 SVM 和增强型 PCP 特征的和弦识别

和弦识别的普遍算法简说

依据音乐理论知识于 1999 年将信号能量压缩到乐曲的 12 个音级上，提出使用12 维的音级轮廓特征音级轮廓（Pitch Class Profile, PCP）作为和弦特征进行模式匹配来识别和弦。在和弦特征方面提出了 HPCP（Harmonic PCP）特征，将其用于和弦识别的键估计系统中并取得了 66.7% 的正确键估计，应用谐波积光谱与 PCP 特征相结合的 EPCP（Enhanced PCP）特征同传统 PCP 特征相比，具有相同根音的和弦具有更好的识别率。当然还有文献结合人耳听觉特性和音乐理论提出了新的识别特征 MPCP（Mel PCP），克服了PCP 特征在低频段特征模糊和峰值处容易发生混倄的缺陷等。
对于和弦分类模型的选择，除模板匹配方法外， MPCP（Mel PCP）采用了条件随机场分割方法，该方法对观测序列没有独立性要求，具有表达长距离依赖性和交叠性特征的能力，缺点是运行时间长；采用神经网络进行和弦识别，可以有效地避免噪声对和弦识别率的影响，但该方法只能识 别有限的歌曲；此外，还有文献说到将统计学方法隐马尔可夫模型（Hidden Markov Model, HMM）应用于和弦的分割和识别中，最终的和弦识别率达到了75%。但 HMM 是一种产生式模型需要严格的独立性假设；近年来，有研究者提出将延时隐马尔可夫模型（Duration HMM）应用于和弦识别。

和弦识别流程

和弦的自动识别主要包括 2 个阶段：特征提取与和弦识别。
使用节拍跟踪同步提取基于瞬时频率的音级特征 PCP，然后将这些特征输入到结构化支持向量机 SVM 中，输出和弦标签，最后同标准和弦标签比对完成和弦的识别。

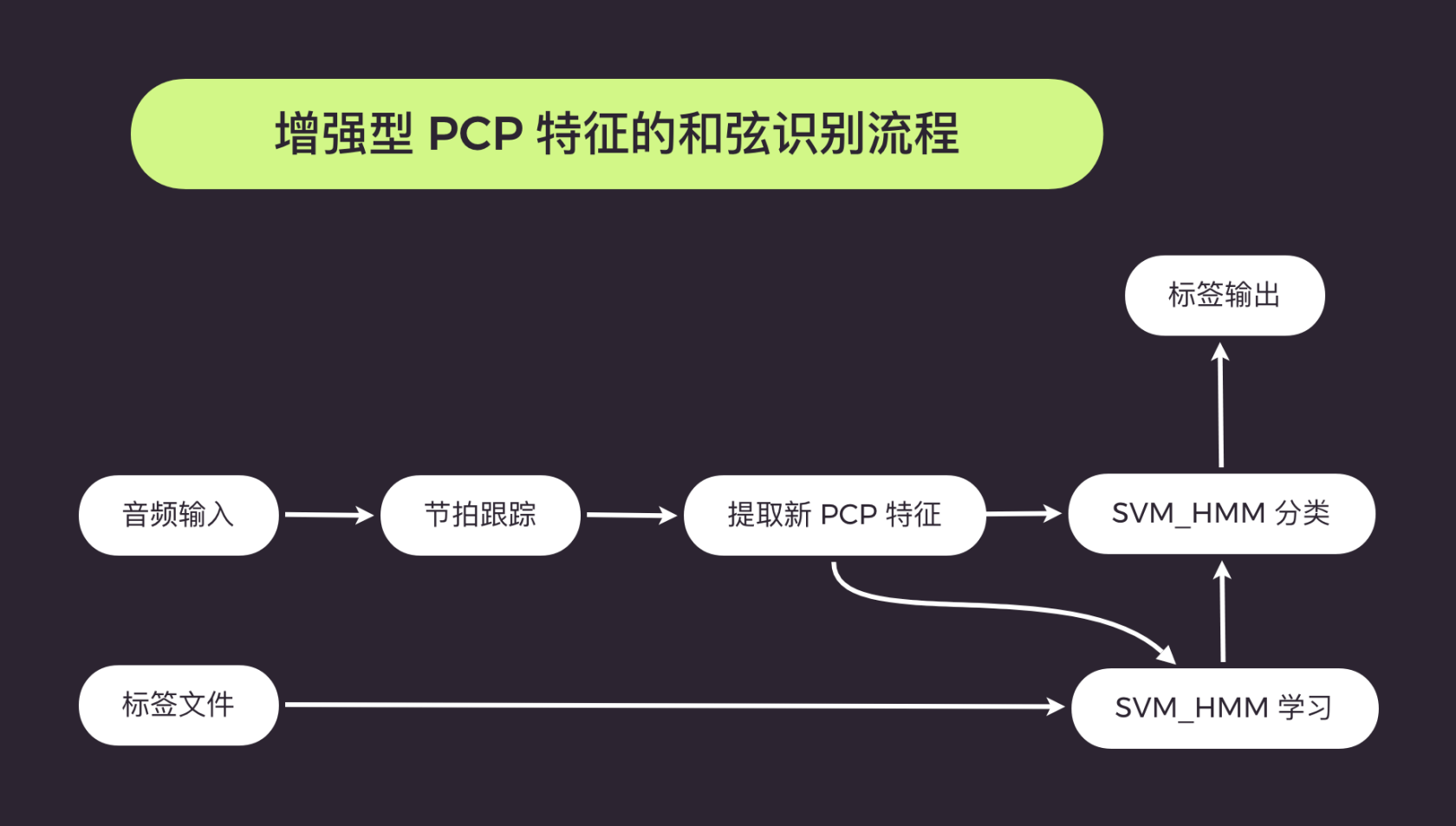
信号特征提取

信号特征的计算由节拍跟踪和 PCP 特征计算 2 个部分组成。
首先通过节拍跟踪获取与节拍构成相符的音频节拍点信息，然后计算出每个节拍间隔内的音级特征 PCP。

节拍跟踪

节拍跟踪用于获取音乐信号中的节拍信息，确定每个节拍在信号中的大致时间位置。它是自动伴奏及转录、计算机辅助音频编辑以及音乐相似性等应用的基础，同步节拍特征也是归一化不同音乐版本之间速率变化的一种很好的途径。
这里采用了「动态规划（DP）节拍跟踪算法」

音频输入\to FFT\ 变换获取起始点能量包络\to 自相关最佳速率估计\to 节拍检测

首先需将音频信号进行快速傅里叶变换（Fast Fourier Transform, FFT），通过一个权重矩阵将傅立叶频谱变换成 40 维 Mel 频谱。计算每一维频谱沿时间轴的一阶差分（只有起始点信息），将整个频谱内的值相加，滤除直流后得到起始能量包络。
然后对整个信号的起始能量进行自相关运算，并在其对数域上加高斯窗获取单一主峰值，将自相关中最大的滞后值作为最佳的速率估计。
最后将起始能量包络和全局速率输入节拍检测模块，通过动态规划算法获取节拍时间位置信息，完成节拍跟踪。

基于节拍的增强型 PCP 特征的提取

第一部分

音级特征 PCP 是音乐信息检索中广泛使用的一种信号特征。在基于瞬时频率 IF 的音级频谱中通过估计瞬时频率 IF 的光谱区域可以从噪声中区分音调元素，同时处理调谐中的差异。

结合音高频率倒谱系数 PFCC，改进了基于 IF 的 PCP 特征的提取算法，这是一种对乐器类型以及音色变化更具鲁棒性的音级特征 PCP。

将经分帧处理后的音频信号进行 FFT 变换得到每一帧的信号能量 E，对差分相位进行求导，得到代表音调的瞬时频率 IF。这时可以采用类似于 Mel 尺度的音调尺度\color{red}\lg(C\times Ε+1)代替 E，C表示音高正常数，在实验中取C=100。 然后对使用对数表示的音调进行 DCT 变换获取 PFCC 系数， 只保留上层PFCC 系数并对其进行 DCT 逆变换得到变换后的音调向量，记做\color{red}\lg E。对能量进行对数压缩是考虑到声音强度的对数感。

第二部分

进行频谱映射。按照音乐理论中的平均律以对数方式将变换后的音调向量\color{red}\lg E映射为新的音级特征 PCP，映射公式：

\displaystyle p(k)=12\times\lg\left(\frac{k\times f_s}{N\times f_r}\right)\bigg|\mathrm{mod}12\\{}\\ f_s=采样率\\{}\\ f_s/N=频率间隔\\{}\\ f_r=参考频率「对应与十二平均律中的C1音」\\{}\\ k\times f_s/N=每一个分量的频率

忽略八度关系只考虑把频率能量分为 12 个频带，将所有与某一特定音级相对应的频率值的音级分量根据以下公式相加得到一个 12 维的音级向量 PCP：

\displaystyle PCP=\sum_{k:p(k)=p}|\lg E(k)|,\ p=1,2,\cdots,12

第三部分

根据节拍跟踪得到的节拍点计算每个节拍间隔内 PCP 的平均值作为基于节拍的音级特征：

\displaystyle \overline{PCP}=\frac{1}{M}\sum_{m=1}^MPCP(p),p=1,2,\cdots,12\\{}\\ M=每个节拍内的帧数

选用不同乐器演奏同一首乐曲时得到的音级 PCP 光谱特征图：

A 乐器弹奏时的传统 PCP 光谱图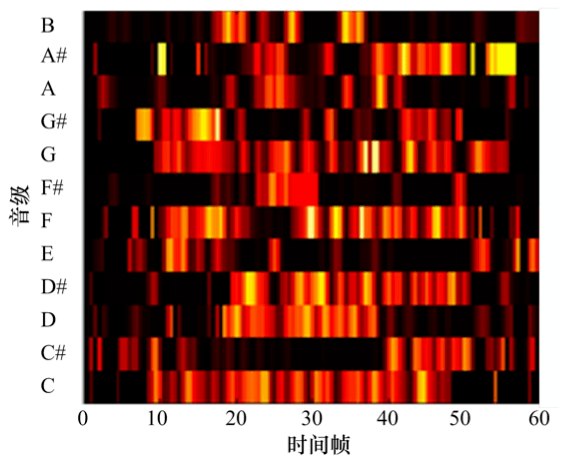

B 乐器弹奏时的传统 PCP 光谱图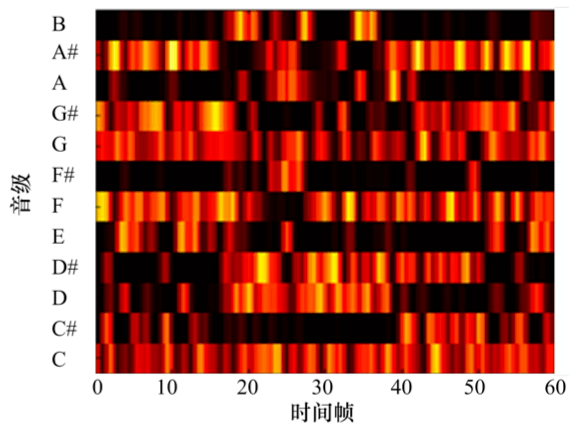

A 乐器弹奏时的增强型 PCP 光谱图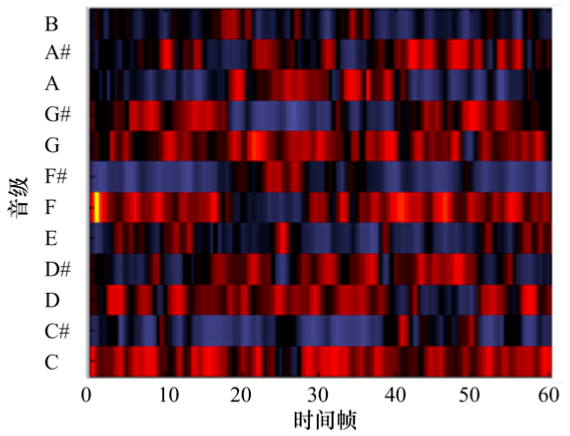

B 乐器弹奏时的增强型 PCP 光谱图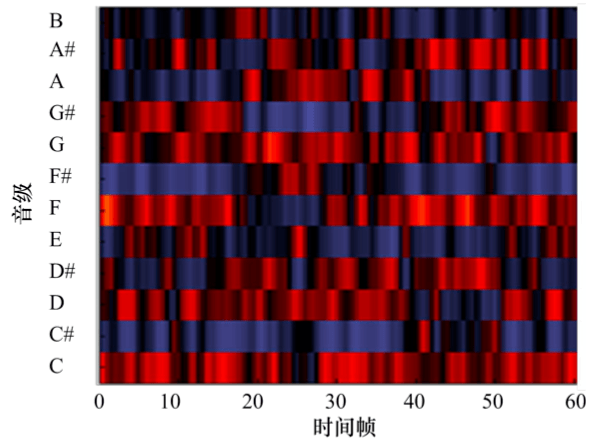

通过 A B 乐器弹奏时的增强型 PCP 光谱图来看，光谱特征之间的差异更小，说明了增强型的 PCP 特征对不同乐器的鲁棒性更强。

到此增强型 PCP 特征算法的计算完毕，接下来就是「结构化的支持向量机」了。

本作品采用《CC 协议》，转载必须注明作者和本文链接