golang实现二倍均值算法和抢红包

对抢红包，大家肯定不陌生，但是，有想过抢红包是如何实现的嘛？
首先，我们得明确一下需求和需求的限制条件。红包主要有三点限制
a.抢到的总额 = 红包的总额，不能多也不能少了
b.最小值是0.01元，即每个人都有份
c.每个人抢到的红包金额，尽量平均

假设总金额是M元，N个人，每次抢的金额=(0, (M/N) *2)，比如，还是之前说的条件，金额100，人数10，
第一个人抢的金额是 (0,20)，抢到的数值，根据正态分布，应该是10左右，远低于10的概率很小，同样远大于10的概率和很小，这里假设第一个人抢到的数值是10；
第二个人抢的金额是(0,90/9 *2)=(0,20)，同第一个人，第二个人红包金额也应该是10附近；
剩下的人，以此类推。
查阅了“微信红包的架构设计”，里面就是使用的这个方法。但是，这个算法，也不是完美的，假如第一个人抢到15，第二个人的范围是(0,18.89)，假如第二个人又抢到很高，那对后面的人是不利的

接下里我们就看看在golang当中如何来实现这个二倍均值算法吧

package main

import (
    "fmt"
    "math/rand"
    "time"
)

func main() {
    //10个人 抢10000分  也就是10个人抢100块钱
    count,amount := int64(10),int64(10000)
    remain := amount
    sum := int64(0)
    for i := int64(0);i<count;i++ {
        x := DoubleAverage(count-i, remain)
        remain -= x
        sum += x
        fmt.Println(i+1,"=",float64(x)/float64(100),", ")
    }
    fmt.Println()
    fmt.Println("总和是:",sum)
}

//提前定义能抢到的最小金额1分
var min int64 = 1
//二倍均值算法
func DoubleAverage(count,amount int64) int64 {
    if count == 1 {
        return amount
    }
    //计算出最大可用金额
    max := amount - min*count
    //计算出最大可用平均值
    avg := max / count
    //二倍均值基础上再加上最小金额 防止出现金额为0
    avg2 := 2 * avg + min
    //随机红包金额序列元素，把二倍均值作为随机的最大数
    rand.Seed(time.Now().UnixNano())
    x := rand.Int63n(avg2) + min
    return x
}

看一下结果喽：

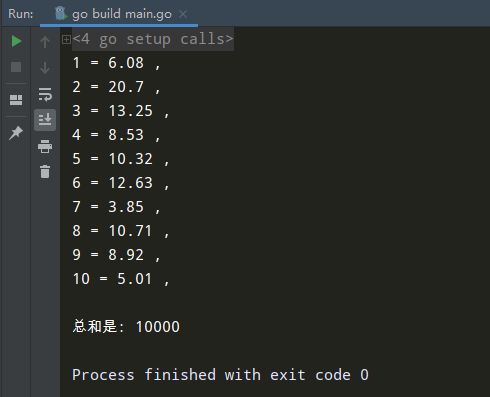
本作品采用《CC 协议》，转载必须注明作者和本文链接