基音周期估计--Yin
介绍
从本文开始,将会开始一系列的语音特征方面的介绍。第一个介绍的语音特征就是基音周期,当发浊音的时候,此时会引起声带的振动,而这个振动会呈现一定的周期性,即基音周期,基音周期的倒数叫基频(fundamental frequency,f0)。简言之,就是去求一个非完全周期函数的近似周期。基音周期用途非常广泛,可以用来检测语音噪声、特殊声音检测、男女判别,说话人识别等。针对于基音周期估计系列,主要介绍两个经典的在时域估计基音周期的方法,Yin以及pYin。本文着重介绍Yin,下一篇介绍pYin。
Yin
时域内的基音周期估计方法主要是去找语音波形的最小正周期,主要是借助于自相关函数。Yin方法求解基音周期主要有如下几个步骤,
首先是计算自相关函数(ACF),Yin采用差函数的形式
d_{t}(\tau)=\sum_{j=t}^{t+W-1}(x_{j}-x_{j+\tau})^2
其中W表示窗的点数。对于差函数而言,峰谷所对应的时延\tau可以表示周期。做减法的优点在于:如果信号幅度在逐渐增大,那么信号往后平移的越多,与原信号相乘的时候结果就会越大。这样就会导致所估计得到的基音周期过大,对应的基频过小。而减法则避免了这个问题。但是基于减法得ACF同样存在一个问题,就是总会在\tau = 0处取得最小值,将会对估计基音周期产生干扰。因此Yin方法提出了累积均值归一化差值函数,将时延值\tau = 0这种情况单独进行了考虑。
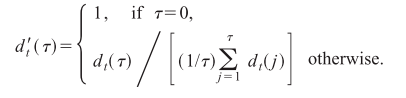
但是累积均值归一化差值函数也会存在一个问题,可能出现下图所示的情况

即峰谷不仅仅出现在上图中的最左边,并且右边的峰谷值比最左边的峰谷值还要小,此时如果直接求累积均值归一化差值函数的最小值,那么很有可能挑选到右边的峰谷,从而估计的基音周期比原基音周期大两倍,即产生了半频错误。所以就引出了Yin论文中的Step 4, 通过设立一个阈值,如果第一个峰谷值比阈值还要大,那么就选择该峰谷值对应的时延作为基音周期。如果没有峰谷值比阈值更大,此时有两种处理方法,要么选相对更小的峰谷要么认为该帧不存在基音周期。最后为了从累积均值归一化差值函数中得到准确的时延,可以先进行插值,然后再搜索得到峰谷对应的时延值。
代码实现
代码主要是参考librosa开源框架库.
import soundfile as sf
import numpy as np
from numpy.lib.stride_tricks import as_strided
def speech_frame(x, frame_length, hop_length, axis=-1):
x = np.ascontiguousarray(x)
n_frames = 1 + (x.shape[axis] - frame_length) // hop_length
strides = np.asarray(x.strides)
new_stride = np.prod(strides[strides > 0] // x.itemsize) * x.itemsize
if axis == -1:
shape = list(x.shape)[:-1] + [frame_length, n_frames]
strides = list(strides) + [hop_length * new_stride]
elif axis == 0:
shape = [n_frames, frame_length] + list(x.shape)[1:]
strides = [hop_length * new_stride] + list(strides)
return as_strided(x, shape=shape, strides=strides)
def cumulative_mean_normalized_difference(y_frames, frame_length, win_length, min_period, max_period):
# 自相关函数和功率谱互为傅里叶变换对.该种方式计算自相关函数可以节省计算量.
a = np.fft.rfft(y_frames, frame_length, axis=0)
# 疑问点1:y_frames[win_length:: -1, :],不知道为啥这样取.
b = np.fft.rfft(y_frames[win_length:: -1, :], frame_length, axis=0)
acf_frames = np.fft.irfft(a * b, frame_length, axis=0)[win_length:]
acf_frames[np.abs(acf_frames) < 1e-6] = 0
energy_frames = np.cumsum(y_frames ** 2, axis=0)
#疑问点2: 不知道为啥这样就能表示r_{t+\tau}
energy_frames = energy_frames[win_length:, :] - energy_frames[:-win_length, :]
energy_frames[np.abs(energy_frames) < 1e-6] = 0
y_yin_frames = energy_frames[0, :] + energy_frames - 2 * acf_frames
yin_numerator = y_yin_frames[min_period: max_period + 1, :]
tau_range = np.arange(1, max_period + 1)[:, None]
cumulative_mean = np.cumsum(y_yin_frames[1 : max_period + 1, :], axis=0) / tau_range
yin_denominator = cumulative_mean[min_period - 1: max_period, :]
yin_frames = yin_numerator / (yin_denominator + tiny(yin_denominator))
return yin_frames
def parabolic_interpolation(y_frames):
parabolic_shifts = np.zeros_like(y_frames)
parabola_a = (y_frames[:-2, :] + y_frames[2:, :] - 2 * y_frames[1:-1, :]) / 2
parabola_b = (y_frames[2:, :] - y_frames[:-2, :]) / 2
parabolic_shifts[1:-1, :] = -parabola_b / (2 * parabola_a + tiny(parabola_a))
parabolic_shifts[np.abs(parabolic_shifts) > 1] = 0
return parabolic_shifts
def localmin(x,axis = 0):
paddings = [(0, 0)] * x.ndim
paddings[axis] = (1, 1)
x_pad = np.pad(x, paddings, mode="edge")
inds1 = [slice(None)] * x.ndim
inds1[axis] = slice(0, -2)
inds2 = [slice(None)] * x.ndim
inds2[axis] = slice(2, x_pad.shape[axis])
return (x < x_pad[tuple(inds1)]) & (x <= x_pad[tuple(inds2)])
def tiny(x):
x = np.asarray(x)
if np.issubdtype(x.dtype, np.floating) or np.issubdtype(
x.dtype, np.complexfloating
):
dtype = x.dtype
else:
dtype = np.float32
return np.finfo(dtype).tiny
y, sr = sf.read('q1.wav')
frame_length = 2048
win_length = frame_length // 2
hop_length = frame_length // 4
y_frame = speech_frame(y, frame_length=frame_length, hop_length=hop_length)
fmax = 2000
fmin = 100
trough_threshold = 0.2
min_period = max(int(np.floor(sr / fmax)), 1)
max_period = min(int(np.ceil(sr / fmin)), frame_length - win_length - 1)
yin_frames = cumulative_mean_normalized_difference(y_frame, frame_length,
win_length, min_period, max_period)
parabolic_shifts = parabolic_interpolation(yin_frames)
is_tough = localmin(yin_frames, axis=0)
is_tough[0, :] = yin_frames[0, :] < yin_frames[1, :]
is_threshold_trough = np.logical_and(is_tough, yin_frames < trough_threshold)
global_min = np.argmin(yin_frames, axis=0)
yin_period = np.argmax(is_threshold_trough, axis=0)
no_trough_below_threshold = np.all(~is_threshold_trough, axis=0)
yin_period[no_trough_below_threshold] = global_min[no_trough_below_threshold]
yin_period = (
min_period
+ yin_period
+ parabolic_shifts[yin_period, range(yin_frames.shape[1])]
)
f0 = sr / yin_period
print(f0)其中q1.wav的波形图,语谱图以及频率响应如下图
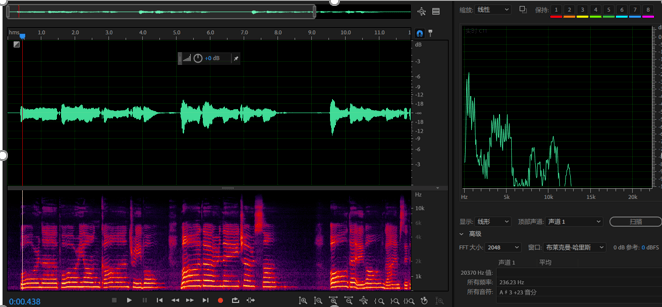
在红线处,其基频大约在237hz,和估计的基本吻合.
本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu




请问博主,q1.wav文件方便给一下吗