原理

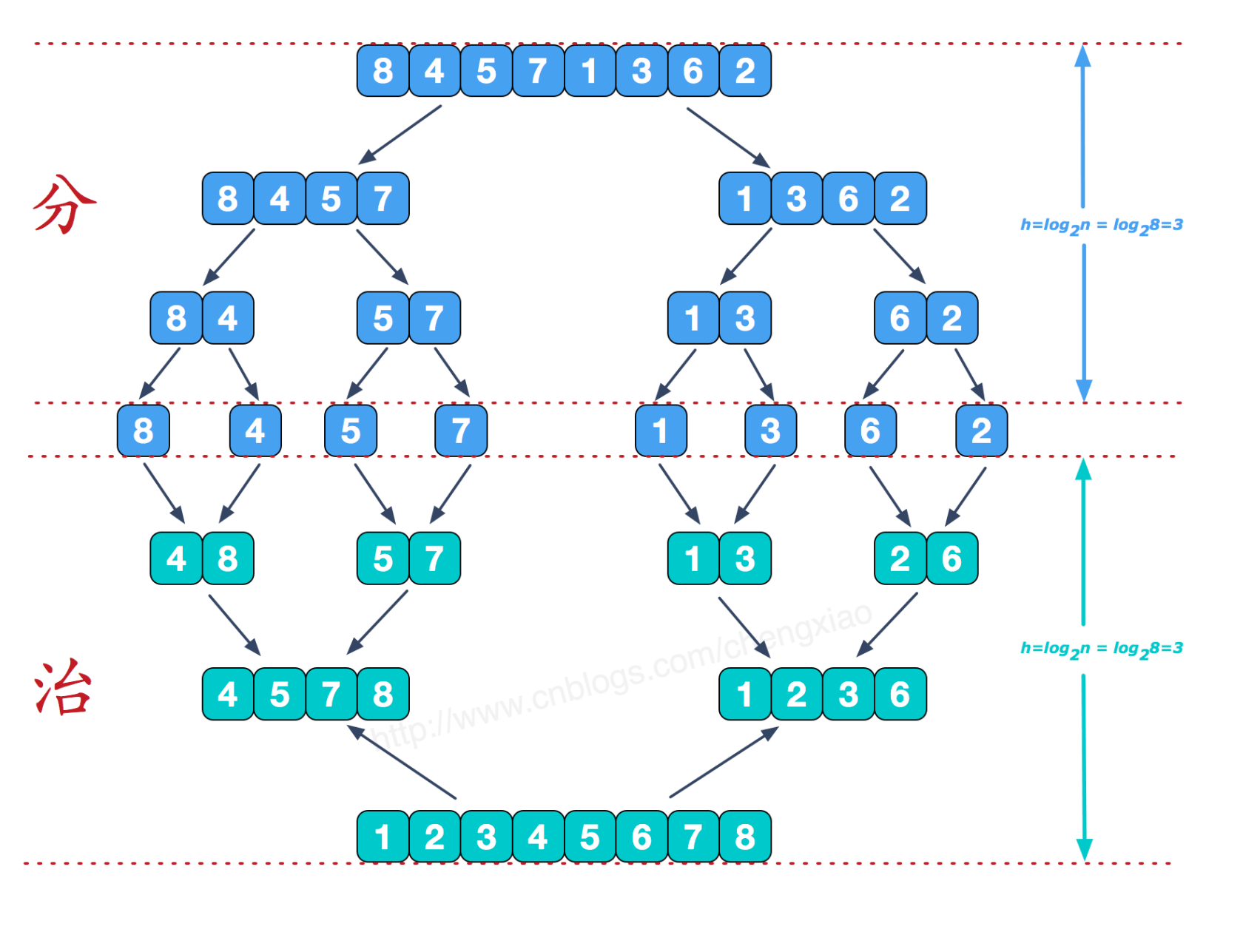
归并排序采用的分而治之的思想，就是把大的问题分成很多个小问题来解决。具体来说就是把一个数组分成 k 份，再依次往下对每一份继续切分为 k 份，直到每一份只剩余一个数字，然后再逐级合并，合并的时候排序，最终得到一个有序的数组。

当 k 取值为 2 时，又叫做 二路归并排序。

步骤

1. 先将原始数组分割为 2 份。
2. 再将这 2 份传入递归函数接着分割。
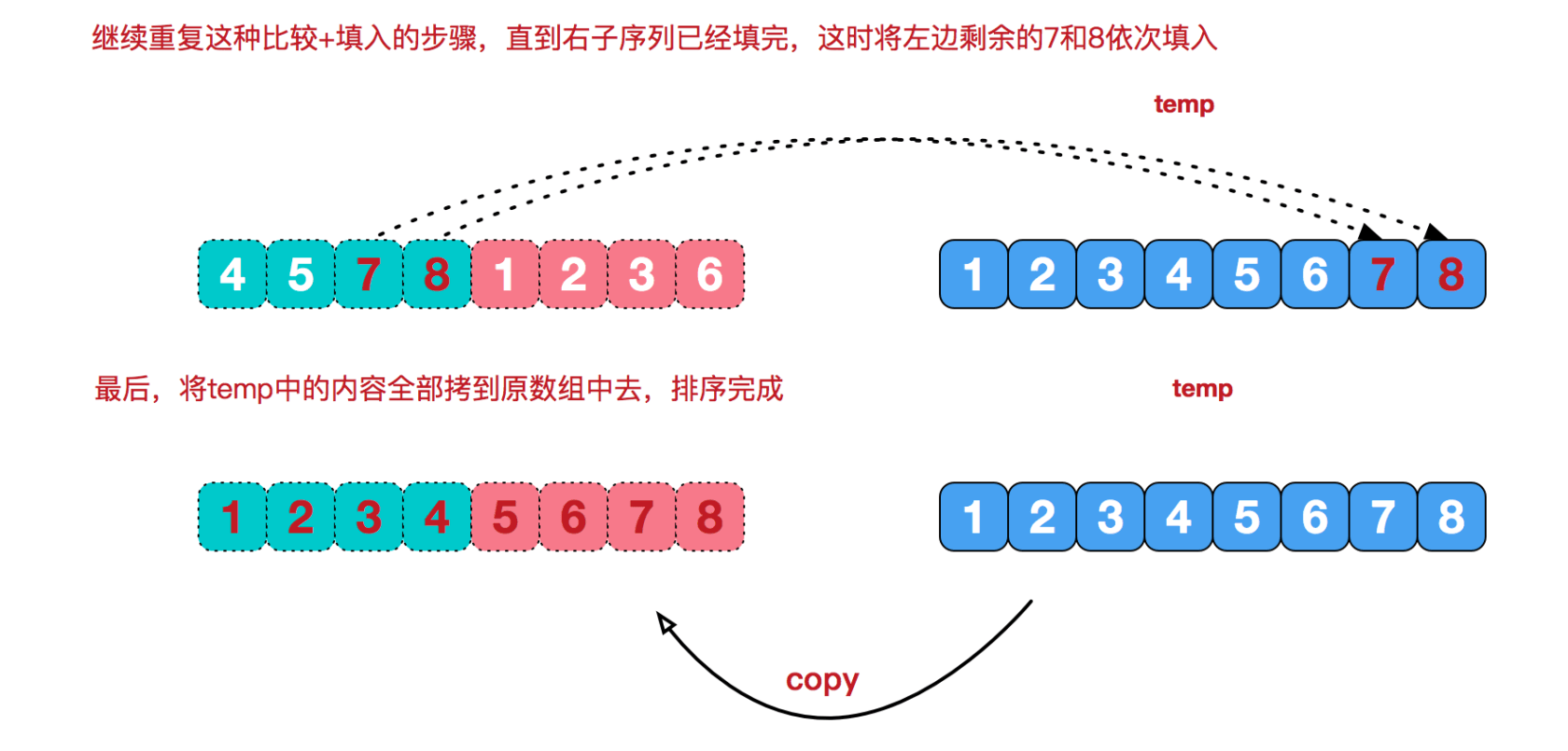
3. 将递归函数返回的数组做归并处理，归并的时候由于两侧的数组都是有序的，所以可以循环比较两侧数组的最小值，插入到一个新的归并数组中，这样归并的时间复杂度最低，为 O(n)。

此图来自：runoob.com 归并排序

代码

<?php declare(strict_types=1);

class Algorithm
{
    public function mergeSort(array $s): array
    {
        $n = count($s);
        if ($n < 2) return $s;

        $m = intval($n / 2);
        $left = $this->mergeSort(array_slice($s, 0, $m));
        $right = $this->mergeSort(array_slice($s, $m));

        $arr = [];
        while (count($left) && count($right)) {
            if ($left[0] < $right[0]) {
                $arr[] = array_shift($left);
            } else {
                $arr[] = array_shift($right);
            }
        }

        while (count($left))
            $arr[] = array_shift($left);

        while (count($right))
            $arr[] = array_shift($right);

        return $arr;
    }
}

时间复杂度

我们以一个长度为 16 的数组为例，分析其中循环的次数。

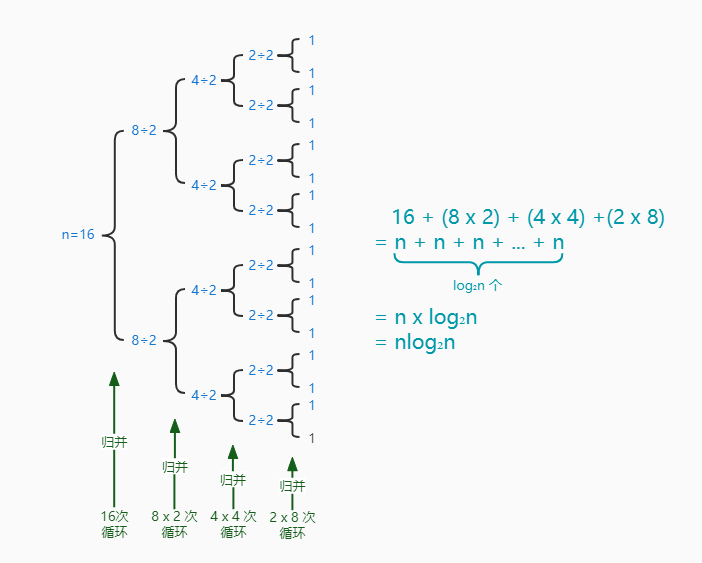
如图所示递归调用的层数是 log₂n，每一层中总的循环次数是 n，所以时间复杂度为：O(nlog₂n)

最好情况（数组本身就是由小到大排序）：O(nlog₂n)

最坏情况（数组本身就是由大到小排序）：O(nlog₂n)

空间复杂度

代码中每一层递归开辟的空间小于等于 n，返回上一层之后下层空间回收，因此空间复杂度为：O(n)

本作品采用《CC 协议》，转载必须注明作者和本文链接