2025-01-15：执行操作可获得的最大总奖励 Ⅰ。用go语言，给定一个整数数组 rewardValues，其中包含 n 个代表奖励值的数字。
你开始时的总奖励 x 为 0，并且所有下标都是未标记状态。你可以进行以下操作若干次：

1.从索引范围 [0, n - 1] 中选择一个未标记的下标 i。

2.如果 rewardValues[i] 大于当前总奖励 x，则将 rewardValues[i] 加到 x 上（即 x = x + rewardValues[i]），并将下标 i 标记为已处理。

请计算并返回通过最佳策略能够获得的最大总奖励。

1 <= rewardValues.length <= 2000。

1 <= rewardValues[i] <= 2000。

输入：rewardValues = [1,1,3,3]。

输出：4。

解释：

依次标记下标 0 和 2，总奖励为 4，这是可获得的最大值。

答案2025-01-15：

chatgpt

题目来自leetcode3180。

大体步骤如下：

1.将给定的奖励数组 rewardValues 排序，假设输入为 [1, 1, 3, 3]，排序后会变成 [1, 1, 3, 3]。

2.初始化两个大整数 f0 和 f1，f0 初始化为 1，f1 初始化为 0。

3.开始遍历排序后的奖励数组 rewardValues。

4.对于每个奖励值 x，创建两个大整数 mask 和 one。mask 用来表示当前处理的奖励的标记位，初始为0；one 表示1。

5.计算当前奖励 x 对应的mask值：mask = (1 << x) - 1。

6.计算 f1 = (f0 & mask) << x。

7.更新 f0 = f0 | f1。

8.返回 f0 中最高位1的位置减1（即 f0.BitLen() - 1）作为最大总奖励值。

总的时间复杂度分析：

• 排序数组的时间复杂度为O(nlogn)，其中 n 为奖励数组的长度。

• 遍历奖励数组的时间复杂度为 O(n)。

所以总的时间复杂度为 O(nlogn)。

总的额外空间复杂度分析：

• 额外创建了一些大整数值，但这些值的个数不随输入数组大小变化，辅助空间复杂度可以忽略不计。
  所以总的额外空间复杂度为 O(1)。

Go完整代码如下：

package main

import (
    "fmt"
    "sort"
    "math/big"
)

func maxTotalReward(rewardValues []int) int {
    sort.Ints(rewardValues)
    f0, f1 := big.NewInt(1), big.NewInt(0)
    for _, x := range rewardValues {
        mask, one := big.NewInt(0), big.NewInt(1)
        mask.Sub(mask.Lsh(one, uint(x)), one)
        f1.Lsh(f1.And(f0, mask), uint(x))
        f0.Or(f0, f1)
    }
    return f0.BitLen() - 1
}


func main() {
    rewardValues := []int{1,1,3,3}
    result := maxTotalReward(rewardValues)
    fmt.Println(result)
}

C完整代码如下：

#include <stdio.h>
#include <stdlib.h>

// 函数用来比较两个整数，供 qsort 使用
int compare(const void *a, const void *b) {
    return (*(int *)a - *(int *)b);
}

// 计算最大总奖励的函数
int maxTotalReward(int *rewardValues, int size) {
    // 排序奖赏值数组
    qsort(rewardValues, size, sizeof(int), compare);

    unsigned long long f0 = 1; // 初始值
    unsigned long long f1 = 0; // 变量 f1

    // 遍历奖赏值数组
    for (int i = 0; i < size; ++i) {
        int x = rewardValues[i];
        unsigned long long mask = (1ULL << x) - 1; // 生成掩码
        f1 = (f0 & mask) << x; // 更新 f1
        f0 |= f1; // 更新 f0
    }

    // 计算 f0 的位长度并返回
    int maxReward = 0;
    while (f0 >= (1ULL << maxReward)) {
        maxReward++;
    }

    return maxReward - 1; // 返回最大奖励
}

int main() {
    int rewardValues[] = { 1, 1, 3, 3 };
    int size = sizeof(rewardValues) / sizeof(rewardValues[0]);
    int result = maxTotalReward(rewardValues, size);
    printf("%d\n", result); // 输出结果
    return 0;
}

C++完整代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>

int maxTotalReward(std::vector<int>& rewardValues) {
    // 排序奖赏值数组
    std::sort(rewardValues.begin(), rewardValues.end());

    unsigned long long f0 = 1; // 初始值
    unsigned long long f1 = 0; // 变量 f1

    // 遍历奖赏值数组
    for (int x : rewardValues) {
        unsigned long long mask = (1ULL << x) - 1; // 生成掩码
        f1 = (f0 & mask) << x; // 更新 f1
        f0 |= f1; // 更新 f0
    }

    // 计算 f0 的位长度并返回
    return static_cast<int>(std::log2(f0)); // 使用 log2 计算位长度
}

int main() {
    std::vector<int> rewardValues = {1, 1, 3, 3};
    int result = maxTotalReward(rewardValues);
    std::cout << result << std::endl; // 输出结果
    return 0;
}

Python完整代码如下：

# -*-coding:utf-8-*-

import math

def max_total_reward(reward_values):
    reward_values.sort()
    f0, f1 = 1, 0
    for x in reward_values:
        mask, one = 0, 1
        mask = (one << x) - 1
        f1 = (f0 & mask) << x
        f0 |= f1
    return f0.bit_length() - 1

if __name__ == "__main__":
    reward_values = [1, 1, 3, 3]
    result = max_total_reward(reward_values)
    print(result)

JavaScript完整代码如下：

function maxTotalReward(rewardValues) {
    rewardValues.sort((a, b) => a - b);
    let f0 = BigInt(1);
    let f1 = BigInt(0);

    for (let x of rewardValues) {
        let mask = BigInt(1) << BigInt(x);
        mask -= BigInt(1);
        f1 = (f0 & mask) << BigInt(x);
        f0 |= f1;
    }

    return f0.toString(2).length - 1;
}

const rewardValues = [1, 1, 3, 3];
const result = maxTotalReward(rewardValues);
console.log(result);

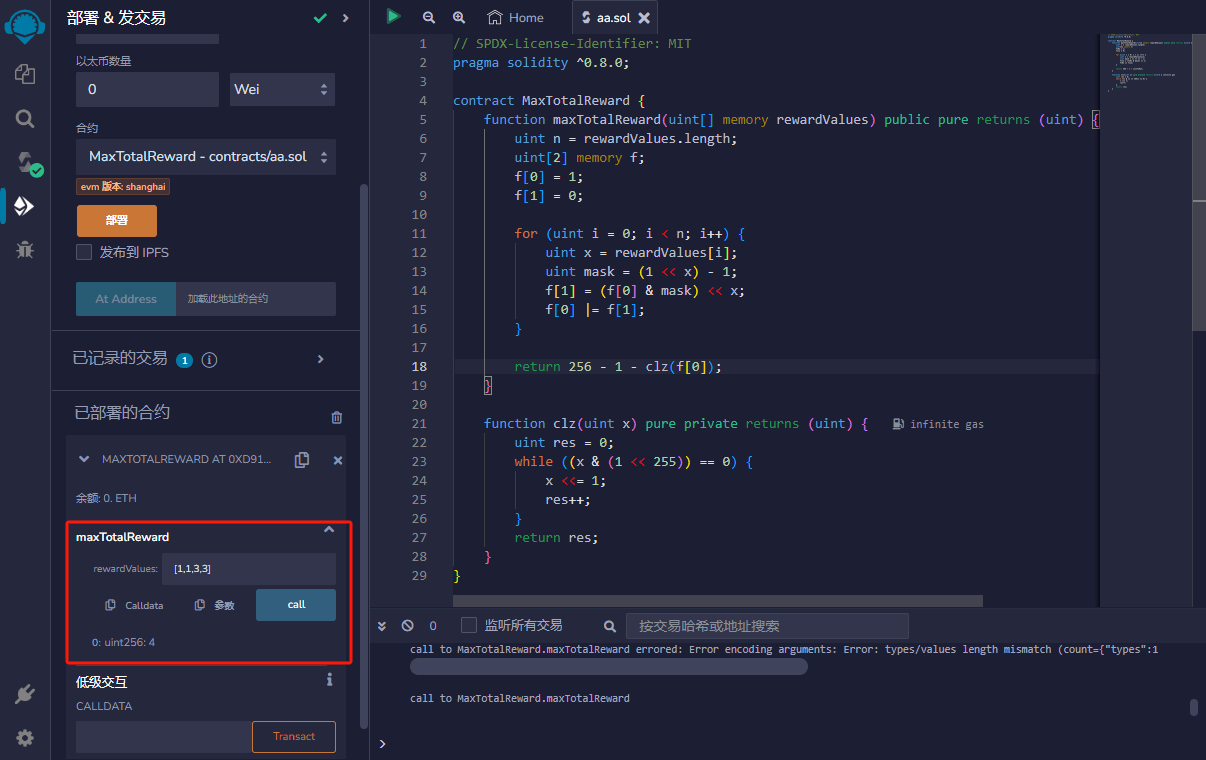
Solidity完整代码如下：

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;

contract MaxTotalReward {
    function maxTotalReward(uint[] memory rewardValues) public pure returns (uint) {
        uint n = rewardValues.length;
        uint[2] memory f;
        f[0] = 1;
        f[1] = 0;

        for (uint i = 0; i < n; i++) {
            uint x = rewardValues[i];
            uint mask = (1 << x) - 1;
            f[1] = (f[0] & mask) << x;
            f[0] |= f[1];
        }

        return 256 - 1 - clz(f[0]);
    }

    function clz(uint x) pure private returns (uint) {
        uint res = 0;
        while ((x & (1 << 255)) == 0) {
            x <<= 1;
            res++;
        }
        return res;
    }
}

本作品采用《CC 协议》，转载必须注明作者和本文链接