纯数学问题, 请在座的大学生秒杀这道初中题 - -
如图, 已知 O, A 两点坐标以及B点y2坐标, 现在需要以O 为圆心旋转角T度, 使A点转至B点. 求角度T.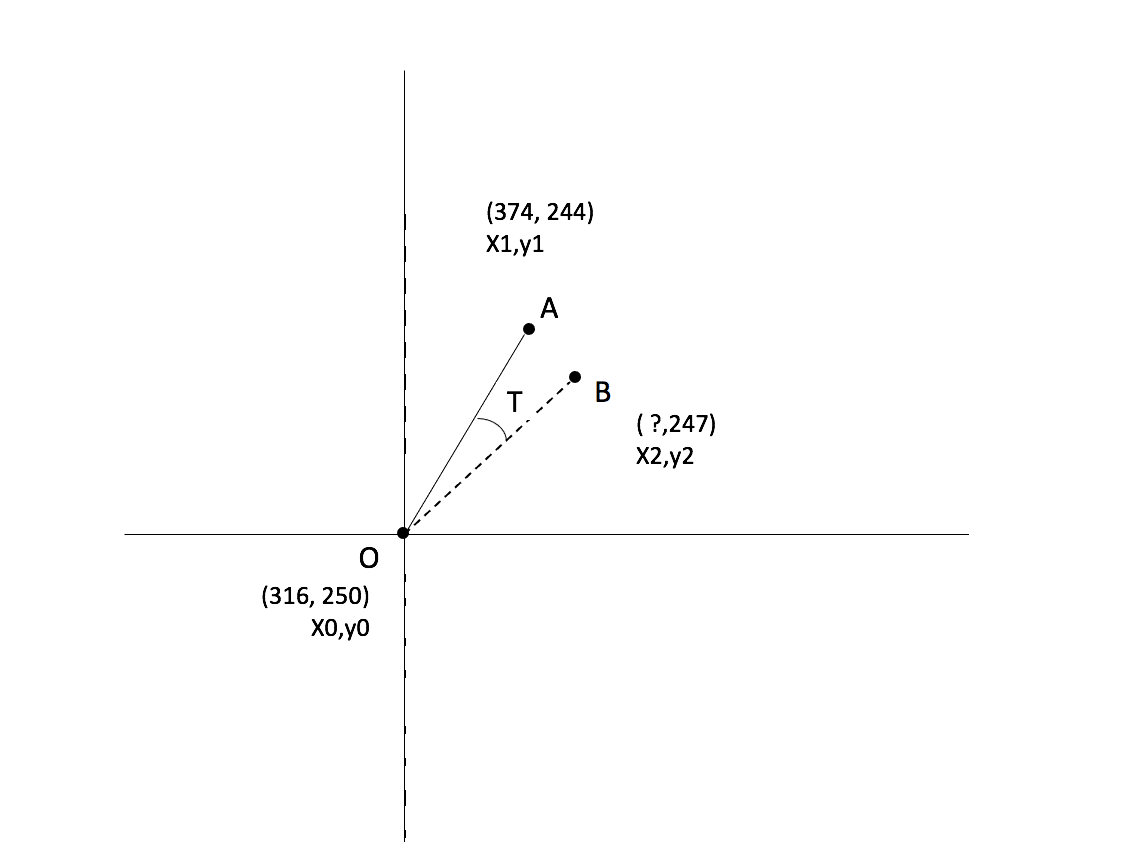
奈何本人三角函数 向量 微积分等数学知识是体育老师教的, 脑中东拼西凑的数学知识得出:
y2 =y0 + (y1-y0)CosT + (x1-x0)SinT
//得
6CosT - 58SinT - 3 =0第一: 算到这不会算了, 第二: 不知道结论是否正确
为了维护大学生的荣耀 只能来论坛求助各路大神了, 大学生一生要强!!
已知问题条件:
- 转动不会超过90度
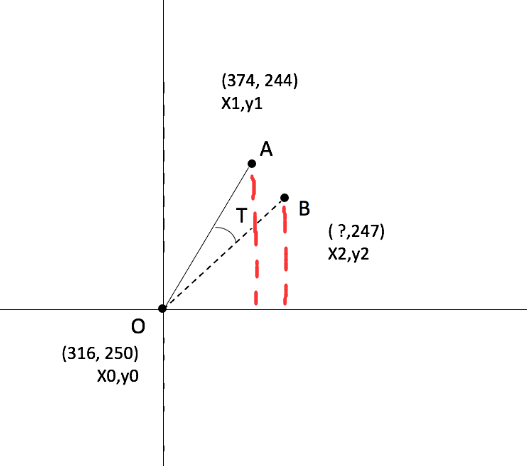如果我没记错的话，这应该是高中甚至初中的知识，求两个直接三角形的角度；当然了，我的数学知识已经全部还给老师了 :stuck_out_tongue_closed_eyes: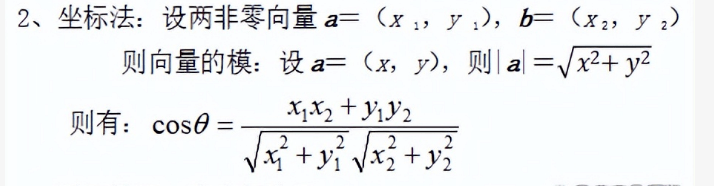
关于 LearnKu
粤公网安备 44030502004330号
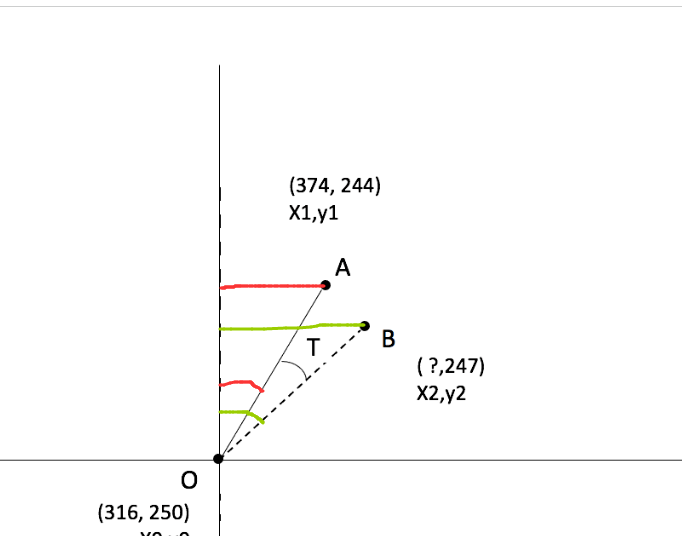
A 的角度 \tan A = \frac { 374 - 316 } { 250 - 244 }
B 的角度 \sin B = \frac{250-247}{\sqrt{58^{2} + 6^{2}}}
T 的角度就是 \tan A - \sin B
我也是网上找的，直角三角形知道两边求角度_每日一讲：解直角三角形（3.21）
如果用向量计算，因为有坐标，所以可以用坐标法:
\cos T = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^{2} + y_{1}^{2}}\sqrt{x_{2}^{2} + y_{2}^{2}}}
这种方式可能更适合用代码来实现，毕竟只有 x_{2} 是不确定的，直接把 x_{2} 当成传进来的参数就可以了