神经网络

Tresdin 的个人博客 / 1352 / 6 / 创建于 5年前 / 更新于 5年前

因为没有找到显示上标的办法，图片也会被强制换行，有几个符号需要给浏览器装一个显示 latex 公式的插件才能正常显示, Math Anywhere for chrome

开局一张图，内容全靠编，本文内容基本是围绕图3 展开的

阅读第1节需要微积分基础

第2节是对第一节内容的逐句翻译, 代码非常啰嗦, 而且时间复杂度是 O(n^4), 对代码有洁癖的同学可以按照 1-> 5-> 3 的顺序阅读

第3节不需要计算微积分，了解概念即可

阅读第5节需要线性代数基础

考虑到矩阵微分比较复杂，且对于理解神经网络不是必须的，放到了比较靠后的位置

因为我没有在别的地方找到以均方差为误差函数的神经网络实现细节，所以给出了全部的计算细节，如果你算的结果和本文不一致（大概率是我打错了），请查看代码

参考书目是我参考的书，并没有强烈推荐，淘宝链接是随机点开的，非广告。实际上《MATLAB神经网络应用设计-第2版》和《矩阵分析与应用-第1版》已经停印很久了，并不建议购买

本文主要参考: MIT 6.034, Lecture 12A: Neural Nets （网易的版本少了一课)

经典模型

神经网络做什么

神经网络[1]用于根据特征判断数据是不是某一类的问题，比如：

特征1	特征2	是不是鸟类
有羽毛	会飞	是
没有羽毛	不会飞	不是
有羽毛	不会飞	?

神经元

神经元模型如下 (图1):

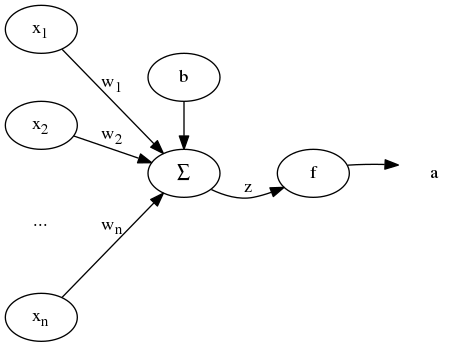
图1-神经元

神经元的输入为 [x₁, x₂, ..., x_n] , 对每一项 x_i 乘以权重 w_i 以及偏置单元 b 求和得到加权和 z, 通过激活函数(传递函数) f, 得到输出 f(z) = a。为了计算简便, 令 x₀ = 1 , w₀ = b, 输出为:

$a = f(z) = f(\\sum\_{i=0}^{n}x\_{i}w\_{i}).$

在经典模型中，激活函数为 sigmoid 函数，其定义及导数如下：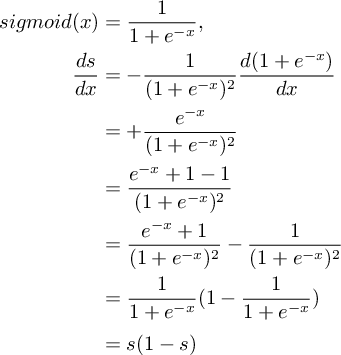

sigmoid 图像如下 (图2):

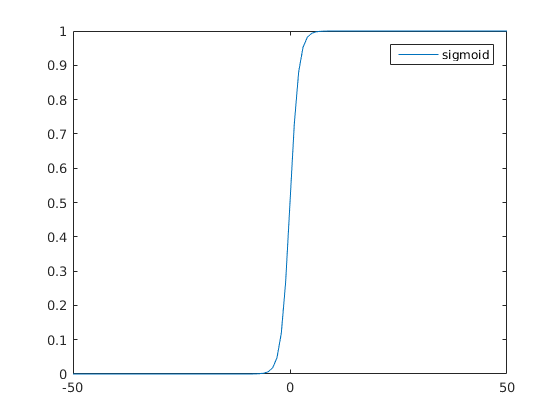
图2-sigmoid

sigmoid 函数的作用是将离散的输入压缩为 (0, 1) 之间的连续值，使离散函数可导，且其导数可以完全用因变量表示，方便计算。

神经网络

多个神经元组成神经网络 (图3):

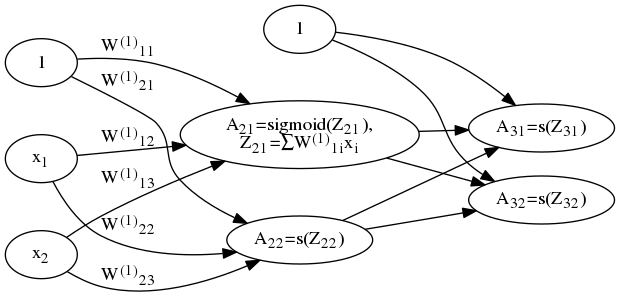
图3-神经网络

神经网络中第一层称为输入层，最后一层称为输出层，中间的层称为隐藏层。对于图3所示网络,总共有 3 层，输入层 L1 = {x₁, x₂, ..., x_n}, 输出层 L3, 和一个隐藏层 L2。从第1层到第2层的参数矩阵为 $W^{(1)}$ , 第2层到第3层的参数矩阵为 $W^{(2)}$ 。参数矩阵形式如下：

$\\vec{W}^{(1)} = \\begin{bmatrix} W^{(1)}\_{11} & W^{(1)}\_{12} & W^{(1)}\_{13} \\\\ W^{(1)}\_{21} & W^{(1)}\_{22} & W^{(1)}\_{23} \\\\ \\end{bmatrix} \\\\ \\vec{W}^{(2)} = \\begin{bmatrix} W^{(2)}\_{11} & W^{(2)}\_{12} & W^{(2)}\_{13} \\\\ W^{(2)}\_{21} & W^{(2)}\_{22} & W^{(2)}\_{23} \\\\ \\end{bmatrix}$

以上是一个糟糕的例子，看不出 $W^{(l)}$ 的大小，实际上 $W^{(l)}$ 大小为 n_{l + 1} x (n_l + 1) 。

前向传递

对于图3所示网络，考虑一组输入的情况，记第 l 层 sigmoid 单元的输入为 $Z^{(l)}$ ,输出为 $A^{(l)}$ , 由输入及参数计算输出: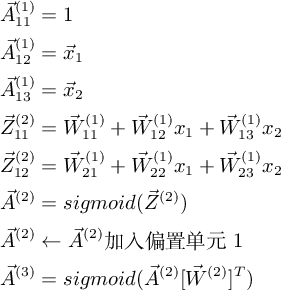
file
因为计算是从前向后进行的，称为前向传递。

损失函数

定义输出层输出 $A^{(3)}$ 和样本值 y 的均方差为损失函数(代价函数):

$J = \\frac{(\\vec{A}^{(3)} - \\vec{y})^2}{2m} \\tag{1.1} \\\\$

考虑结构风险最小化，加入正则化项:

$J\_{srm} = \\frac{(\\vec{A}^{(3)} - \\vec{y})^2}{2m} + \\frac{\\lambda}{2m} \\sum\_{l}\\sum\_{i}\\sum\_{j}(\\vec{W}\_{ij}^{(l)})^2 \\tag{1.2} \\\\$

另一个常见的损失函数是由最大似然估计[2]得出的:

$J = -\\frac{1}{m}\[\\sum\_{i=1}^{m}\\sum\_{j=1}^{n}y\_{j}^{(i)} \\ln{s(z^{(i)})\_j} + (1 - y^{(i)}\_j \\ln{(1 - s(z^{(i)}\_j))}\] + \\frac{\\lambda}{2m} \\sum\_{l} \\sum\_{i} \\sum\_{j} (W^{(l)}\_{ij})^2$

反向传递

应用链式法则[3]从后向前依次求 J 关于 $W^{(2)}, W^{(1)}$ 的偏导[4]的过程称为反向传递(BP)。因为 BP 的向量化比较复杂，先考虑只有1组输入的情况下的标量结果，即 X 的大小为 1 x n 。先计算 J 关于 $W^{(2)}_{12}$ 和 $W^{(1)}_{12}$ 的偏导: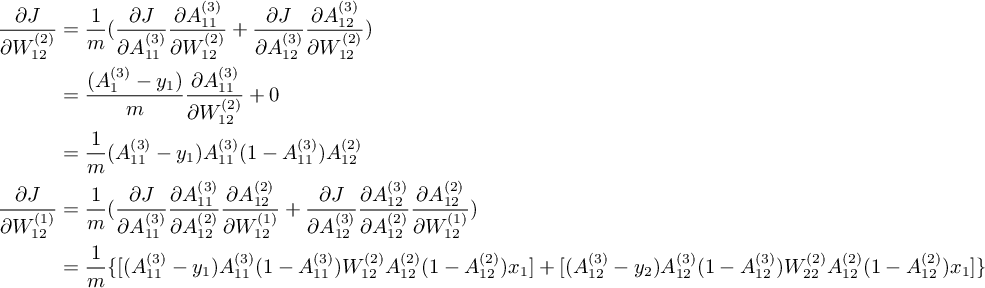
file
类似地应用链式法则，求出全部关于权重的偏导 ( $A^{(2)}_{11} = A^{(1)}_{11} = 1$ ) :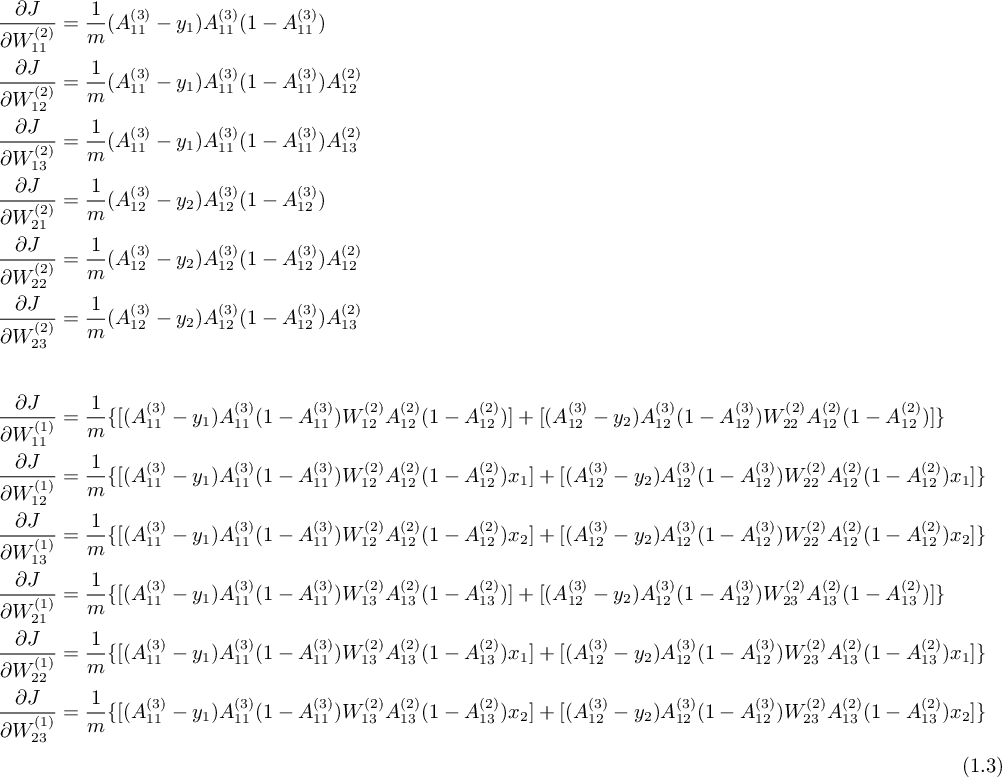
file

对比上式可以看出，在从后向前逐级计算偏导的过程中，存在着可以重复利用的项，所以（线性）增加层数带来算法复杂度的增加是线性的。

正则化项的偏导为:

$\\frac{\\partial{\\frac{\\lambda}{2m} \\sum\_{l}\\sum\_{i}\\sum\_{j}(W\_{ij}^{(l)})^2}}{\\partial{W\_{ij}^{(l)}}} = \\frac{\\lambda}{m} W\_{ij}^{(l)} \\\\$

最后，神经网络的输出和样本值接近意味着 J 尽可能小，利用梯度下降[5]求解优化问题 $argmin{J(W)}$ ,计算权重 :

$\\text{iterate:}\\\\ \\vec{W} \\gets \\vec{W} - \\alpha \\frac{\\partial{J}}{\\partial{\\vec{W}}}$

PHP 实现

准备数据

以图3所示网络对经典的鸢尾花分类。原始数据格式如下:

萼片长(cm)	萼片宽(cm)	花瓣长(cm)	花瓣宽(cm)	分类
5.1	3.5	1.4	0.2	Iris-setosa
4.9	3.0	1.4	0.2	Iris-setosa
...	...	...	...	...
7.0	3.2	4.7	1.4	Iris-versicolor
6.4	3.2	4.5	1.5	Iris-versicolor
...	...	...	...	...
6.3	3.3	6.0	2.5	Iris-virginica
5.8	2.7	5.1	1.9	Iris-virginica
...	...	...	...	...

数据前4列为特征值，最后一列为分类，总共有150行, 每50行为一种鸢尾花（3分类问题）。因为图3所示网络输入和输出单元都只有 2个，即只能处理 2 个特征的 2 分类问题，首先使用 PCA 算法将特征压缩到 2 维, 输出只判断是不是第 1 类。格式如下:

输入特征1	输入特征2	输出
-2.684207	0.326607	0
-2.715391	-0.169557	0
1.464061	0.504190	1

此处不用在意 PCA 是怎么回事, 将2维数据看做原始数据即可。

前向传播

vec2mat($v, $r, $n) 将向量 v 按行展开为 r x n 的矩阵（大多数实现都是按列展开）；
fill2d($r, $c, $v) 生成一个大小为 r x c ，值全为 v 的矩阵；
fp(array $a1, array $w) 使用输入矩阵 a1 和权重矩阵展开后的向量 w 计算输出矩阵。

// ##### 前向传播 ################
function fp(array $a1, array $w)
{
    $m = count($a1);
    $n = count($a1[0]);

    $ws = array_chunk($w, 6);
    $w1 = vec2mat($ws[0], 2, 3);
    $w2 = vec2mat($ws[1], 2, 3);

    $A1 = fill2d($m, 3, 1);
    $a2 = fill2d($m, 2, 0);
    $A2 = fill2d($m, 3, 1);
    $a3 = fill2d($m, 2, 0);

    // 输入加偏执单元
    for ($i = 0; $i < $m; $i++) {
        $A1[$i][0] = 1;
        $A1[$i][1] = $a1[$i][0];
        $A1[$i][2] = $a1[$i][1];
    }

    // compute A2, a3
    for ($i = 0; $i < $m; $i++) {
        // 1 -> 2 层
        // 加权和
        $z11 = $A1[$i][0] * $w1[0][0] + $A1[$i][1] * $w1[0][1] + $A1[$i][2] * $w1[0][2];
        $z12 = $A1[$i][0] * $w1[1][0] + $A1[$i][1] * $w1[1][1] + $A1[$i][2] * $w1[1][2];

        $a2[$i][0] = sigmoid($z11);
        $a2[$i][1] = sigmoid($z12);

        // A2 加入偏置单元
        $A2[$i][0] = 1;
        $A2[$i][1] = $a2[$i][0];
        $A2[$i][2] = $a2[$i][1];

        // 2 -> 3 层
        $z21 = $A2[$i][0] * $w2[0][0] + $A2[$i][1] * $w2[0][1] + $A2[$i][2] * $w2[0][2];
        $z22 = $A2[$i][0] * $w2[1][0] + $A2[$i][1] * $w2[1][1] + $A2[$i][2] * $w2[1][2];
        $a3[$i][0] = sigmoid($z21);
        $a3[$i][1] = sigmoid($z22);
    }

    return $a3;
}

计算损失

a3 是最后一层的输出
y 是样本输出
m 是样本数量
w 是参数矩阵
lambda 是正则化参数

// 计算损失
$J = 0;
for ($i = 0; $i < $m; $i++) {
    $J += pow($a3[$i][0] - $y[$i][0], 2) + pow($a3[$i][1] - $y[$i][1], 2);
}
$J = $J / (2 * $m);

// 加入正则化项
$r = 0;
for ($i = 0; $i < 2; $i++) {
    // $j 从1开始也可以
    for ($j = 0; $j < 3; $j++) {
        $r += pow($w1[$i][$j], 2);
        $r += pow($w2[$i][$j], 2);
    }
}
$r = $r * $lambda / (2 * $m);

// 结构风险最小化损失
$Jsrm = $J + $r;

反向传播

Ai 是第 i 层的输出
mat2vec(array $m) 将矩阵 m 按行展开为向量（大多数实现是按列）

// 初始化 J 对 w2 的偏导
$p2 = fill2d(2, 3, 0);
// 初始化 J 对 w1 的偏导
$p1 = fill2d(2, 3, 0);

for ($i = 0; $i < $m; $i++) {
    $delta1 = 1 / $m * ($a3[$i][0] - $y[$i][0]) * $a3[$i][0] * (1 - $a3[$i][0]);
    $delta2 = 1 / $m * ($a3[$i][1] - $y[$i][1]) * $a3[$i][1] * (1 - $a3[$i][1]);
    $p2[0][0] += $delta1 * $A2[$i][0];
    $p2[0][1] += $delta1 * $A2[$i][1];
    $p2[0][2] += $delta1 * $A2[$i][2];
    $p2[1][0] += $delta2 * $A2[$i][0];
    $p2[1][1] += $delta2 * $A2[$i][1];
    $p2[1][2] += $delta2 * $A2[$i][2];
}
// 加入正则化项的偏导
$p2[0][0] += $lambda / $m * $p2[0][0]; // 这一项不加也可以
$p2[0][1] += $lambda / $m * $p2[0][1];
$p2[0][2] += $lambda / $m * $p2[0][2];
$p2[1][0] += $lambda / $m * $p2[1][0]; // 这一项不加也可以
$p2[1][1] += $lambda / $m * $p2[1][1];
$p2[1][2] += $lambda / $m * $p2[1][2];

for ($i = 0; $i < $m; $i++) {
    $delta1 = 1 / $m * (
        ($a3[$i][0] - $y[$i][0]) * $a3[$i][0] * (1 - $a3[$i][0]) * $w2[0][1] +
        ($a3[$i][1] - $y[$i][1]) * $a3[$i][1] * (1 - $a3[$i][1]) * $w2[1][1]
    ) * $A2[$i][1] * (1 - $A2[$i][1]);

    $delta2 = 1 / $m * (
        ($a3[$i][0] - $y[$i][0]) * $a3[$i][0] * (1 - $a3[$i][0]) * $w2[0][2] +
        ($a3[$i][1] - $y[$i][1]) * $a3[$i][1] * (1 - $a3[$i][1]) * $w2[1][2]
    ) * $A2[$i][2] * (1 - $A2[$i][2]);

    $p1[0][0] += $delta1 * $A1[$i][0];
    $p1[0][1] += $delta1 * $A1[$i][1];
    $p1[0][2] += $delta1 * $A1[$i][2];
    $p1[1][0] += $delta2 * $A1[$i][0];
    $p1[1][1] += $delta2 * $A1[$i][1];
    $p1[1][2] += $delta2 * $A1[$i][2];
}

// 加入正则化项的偏导
$p1[0][0] += $lambda / $m * $p1[0][0]; // 这一项不加也可以
$p1[0][1] += $lambda / $m * $p1[0][1];
$p1[0][2] += $lambda / $m * $p1[0][2];
$p1[1][0] += $lambda / $m * $p1[1][0]; // 这一项不加也可以
$p1[1][1] += $lambda / $m * $p1[1][1];
$p1[1][2] += $lambda / $m * $p1[1][2];

// 偏导矩阵转向量
$p = array_merge(mat2vec($p1), mat2vec($p2));

梯度下降

w 是各权重矩阵展开后组合而成的向量
p 是各偏导矩阵展开后组合而成的向量
alpha 是学习率
返回下降后的权重向量

 // w <- w - alpha * (partial J) / (partial w)
function gradDesc(array $w, float $alpha, array $partial)
{
    $n = count($w);
    for ($i = 0; $i < $n; $i++) {
            $w[$i] = $w[$i] - $alpha * $partial[$i];
    }
    return $w;
}

训练和测试

code/php/run.php 显示了训练和测试的过程

<?php

require("snn.php");

// 初始化迭代次数
$iter = 300;
// 初始化梯度下降参数
$alpha1 = array_pad([], $iter, 0.1); // 固定参数
$alpha2 = range($iter * 0.01, 0, -0.01); // 递减参数
// 初始化正则化参数
$lambda = 1;

// 载入数据
$fx = file('iris-2.data');
$fy = file('iris-y.data');
$y = [];
$x = [];
$xTest = [];
$yTest = [];

// 取样本数据
for ($i = 0; $i < 40; $i++) {
    $x[] = str_getcsv($fx[$i]);
    if (intval($fy[$i]) < 1) {
        $y[] = [1, 0];
    } else {
        $y[] = [0, 1];
    }
}
for ($i = 50; $i < 130; $i++) {
    $x[] = str_getcsv($fx[$i]);
    if (intval($fy[$i]) < 1) {
        $y[] = [1, 0];
    } else {
        $y[] = [0, 1];
    }
}

// 取测试数据
for ($i = 40; $i < 50; $i++) {
    $xTest[] = str_getcsv($fx[$i]);
    $yTest[] = intval($fy[$i]);
}
for ($i = 130; $i < 150; $i++) {
    $xTest[] = str_getcsv($fx[$i]);
    $yTest[] = intval($fy[$i]);
}

// 0 -> [1, 0], 1 -> [0, 1]

// 随机初始化参数矩阵
$w1 = [];
$w2 = [];
for ($i = 0; $i < 2; $i++) {
    $w1r = [];
    $w2r = [];
    for ($j = 0; $j < 3; $j++) {
        $w1r[] = (rand(1, 99) - 50) / 100;
        $w2r[] = (rand(1, 99) -50) / 100;
    }
    $w1[] = $w1r;
    $w2[] = $w2r;
}

// 迭代
$JHistory = [];
$w = array_merge(mat2vec($w1), mat2vec($w2));

for ($i = 0; $i < $iter; $i++) {
    $res = compute($x, $y, $w, $lambda);
    $JHistory[] = $res["J"];
    // 使用固定学习率
    // $w = gradDesc($w, $alpha1[$i], $res["P"]);
    // 使用递减学习率
    $w = gradDesc($w, $alpha2[$i], $res["P"]);
}

// 在测试集上验证
$a3 = fp($xTest, $w);
$JHistory[] = $res["J"];
$hatY = [];
$total = 0;
$correct = 0;

$m = count($xTest);
for ($i = 0; $i < $m; $i++) {
    $arr = $a3[$i];
    // [0, 1]-> 1; [1, 0] -> 0
    if ($arr[0] > $arr[1]) {
        $hat = 0;
    } else {
        $hat = 1;
    }
    $hatY[] = $hat;
    // 比较预测值和实际值
    if ($hat <= intval($yTest[$i])) {
        $correct++;
    }
    $total++;
}
// 输出正确率
echo "Correct: $correct / $total\n";
// output: Correct: 30 / 30

// 保存最终估计值
$csv = fopen("haty.csv", "w");
fputcsv($csv, $hatY);
fclose($csv);

// 保存损失历史
$csv = fopen("historyCost.csv", "w");
fputcsv($csv, $JHistory);
fclose($csv);

经过调节参数最终输出正确稳定到 1。以下为迭代误差图像: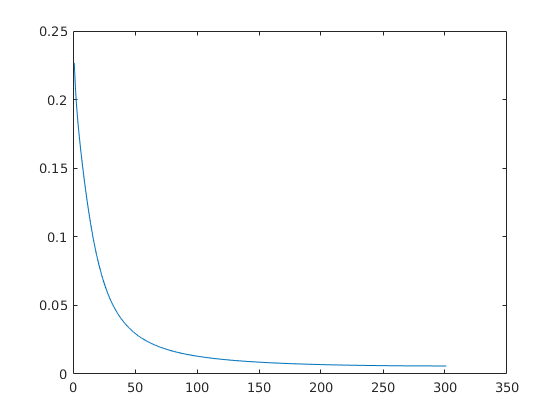
file

使用 API

code/php/useApi.php 使用 fann 扩展对 4 特征鸢尾花分类,

<?php

// 层数
$num_layers = 3;
// 第1层特征数
$num_n1 = 4;
// 第2层特征数
$num_n2 = 3;
// 第3层特征数
$num_n3 = 3;
// 创建标准反向传播神经网络
$fann = fann_create_standard($num_layers, $num_n1, $num_n2, $num_n3);
// 设置隐藏层激活函数为 sigmoid
fann_set_activation_function_hidden($fann, FANN_SIGMOID);
// 设置输出层激活函数为 sigmoid
fann_set_activation_function_output($fann, FANN_SIGMOID);
// 设置训练停止函数为 均方差
fann_set_train_stop_function($fann, FANN_STOPFUNC_MSE);
// 设置训练算法为每次求均方差后更新权重
fann_set_training_algorithm($fann, FANN_TRAIN_BATCH);
// 训练次数
$iter = 1000;
// 用户函数，无
$userFunc = 0;
// 误差小于 $stopError 时停止训练
$stopError = 1E-6;
// 由数据文件进行训练,
fann_train_on_file($fann, 'iris-4-train.data', $iter, $userFunc, $stopError);
// 保存网络
fann_save($fann, 'fann.net');
// 读测试数据
$x = fopen('iris-4-test-x.data', 'r');
// 运行测试
$hat = [];
while ($arr = fgetcsv($x)) {
    $output = fann_run($fann, $arr);
    arsort($output);
    $hat[] = array_keys($output)[0];
}
fclose($x);

// 输出预测值
echo join($hat, ","), PHP_EOL;

/*
 * output:
 * 0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2
 */

// 销毁网络
fann_destroy($fann);

fann 使用的数据格式:

数据用空格和换行分割;
第 1 行 3 个数代表: "样本数", "输入特征数", "输出特征数";
从第 2 行开始，依次为一行输入，一行输出.

    2 4 3
    5.10 3.50 1.40 0.20
    1 0 0
    4.90 3.00 1.40 0.20
    1 0 0

局部最优

梯度下降主要的问题在于，如果使用太大的学习率，损失函数不能收敛，使用太小的学习率，函数将收敛到第一个遇到的局部最小值。局部最小值会随着神经元的增而增加。对于这一问题，本文采用的处理是，学习率从大到小递减（模拟退火）。当隐藏层很多（深度学习网络），使用本文的方法几乎不可能得到全局最优解，许多实现中用遗传算法求优化问题。

向量化实现

向量微分

由以下向量微分公式[6]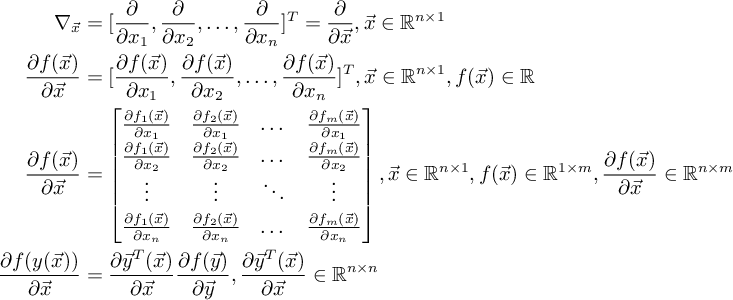
file
和 1.3式, 可以得出前向/反向传播的一般情况。设：
file
那么:
file

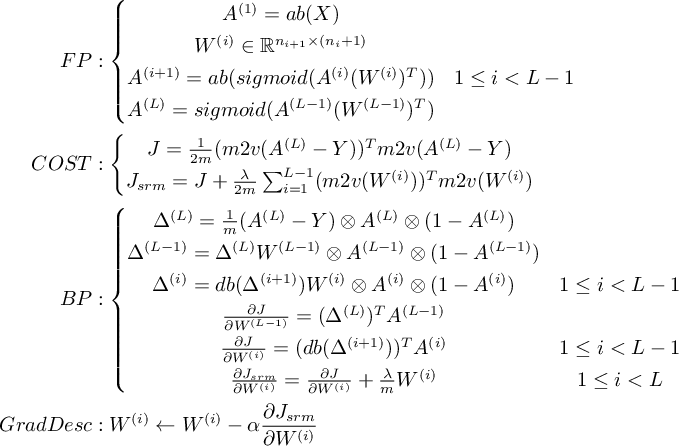
向量微分的性质可以直接推广到矩阵。

矩阵 B = f(A)，求 B 对 A 的导数 ∂B / ∂ A 即是 B 中每个元素分别对 A 中每个元素求导，可以分子 B 按行展开，分母 A 按列展开，或B按列展开，A按行展开，分别求导，使用哪一种展开规则都可以，只要保持一致（当使用不同的规则，有一种要转置）即可。然后将得到的微分单元按展开的规则逆向合并为一个矩阵，再由初等行/列变换化为最简型。

Matlab/Octave 实现

[W, P] = initWeight(X, Y, hiddenLayer) 由输入矩阵 X, 输出矩阵 Y, 和隐藏层数目 hiddenLayer 初始化参数矩阵集合 W 和均方差对 W 的偏导矩阵集合 P

function [W, P] = initWeight(X, Y, hiddenLayer)
% 初始化参数和偏导矩阵%, 隐藏层单元数等于输入层单元数, 全连接
% input:
%     hidden_layer: scalar, number of hidden layer
% output:
%     W: matrix cell array, weigth
%     P: matrix cell array, partial
    n1 = size(X, 2);
    n2 = size(Y, 2);
    for k = 1: hiddenLayer
        W{k} = rand(n1, n1 + 1) - 0.5;
        P{k} = zeros(n1, n1 + 1);
    end
    W{k + 1} = rand(n2, n1 + 1) - 0.5;
    P{k + 1} = zeros(n1, n1 + 1);
end

A = fp(X, W) 由输入矩阵 X 和参数矩阵集合 W 计算每层的输出集合 A

function A = fp(X, W)
% 前向传播
% input:
%     X - matrix cell array
%     W - matrix cell array
% output:
%     A - matrix cell array
    m = size(X, 1);
    A{1} = [ones(m, 1), X];
    for k = 1: length(W) - 1
        A{k + 1} = [ones(m, 1), sigmoid(A{k} * (W{k})')];
    end
    A{k + 2} = sigmoid(A{k + 1} * (W{k + 1})');
end

J = cost(A, Y, W, lambda) 由输出层输出矩阵 X, 样本输出矩阵 Y, 参数矩阵集合 W, 正则化参数 lambda 计算正则化均方差 J

function J = cost(A, Y, W, lambda)
% 计算均方误差
% input:
%     A - matrix
%     Y - matrix
%     W - matrix cell array
%     lambda - scalar
% output:
%     J - scalar
    m = size(Y, 1);
    d = A - Y;
    J = 1 / (2 * m) * d(:)' * d(:);

    % 正则项
    r = 0;
    for k = 1: length(W)
        w = W{k};
        r = r + w(:)' * w(:);
    end
    r = lambda * r / (2 * m);

    % 正则化误差
    J = J + r;
end

P = bp(A, W, Y, lambda) 由每层输出矩阵集合 A, 参数矩阵集合 W, 样本输出矩阵 Y, 正则化参数 lambda 计算均方差对 W 的偏导矩阵集合 P

function P = bp(A, W, Y, lambda)
% 后向传播求偏导
% input:
%     A - matrix cell array
%     Y - matrix
%     J - scalar
% output:
%     P - matrix cell array

% 求每一层的偏导
    m = size(Y, 1);
    l = length(A);
    Delta{l} = 1 / m * (A{l} - Y) .* (A{l} .* (1 - A{l}));
    Delta{l - 1} = Delta{l} * W{l - 1} .* (A{l - 1} .* (1 - A{l - 1}));
    for k = l - 2: -1: 2
        % 偏置单元与前一层的偏导无关
        D = Delta{k + 1}(:, 2: end); 
        Delta{k} = D * W{k} .* (A{k} .* (1 - A{k}));
    end

    % 求权重的偏导
    l = length(W);
    for k = 1: l - 1
        D = Delta{k + 1}(:, 2: end);
        P{k} = D' * A{k};
        % 加入正则化项的偏导
        P{k} = P{k} + lambda / m * W{k};
    end
    P{l} = (Delta{l + 1})' * A{l} + lambda / m * W{l};
end

W = gradDesc(alpha, W, P) 由学习率 alpha, 参数矩阵集合 W, 均方差对 W 的偏导矩阵集合 P 计算梯度下降更新后的参数矩阵集合 W

function W = gradDesc(alpha, W, P)
% 梯度下降
% input:
%     alpha - scalar, learning ratio
%     W - matrix cell array, weight
%     P - matrix cell array, partial
% output:
%     W - matrix cell array, weight
    for k = 1: length(W)
        W{k} = W{k} - alpha * P{k};
    end
end

code/matlab/run.m 使用以上函数测试鸢尾花分类

clear;close;clc;
% 准备数据

% matlab 可以使用 iris_dataset
% ##########################
% [X, Y] = iris_dataset;
% X = X';
% Y = Y';
% ##########################

% octave 需要手动下载数据
% ############################
data = load('iris-150x5.data');
X = data(:, 1:end-1);
y = data(:, end);
yu = unique(y);
yn = length(yu);
Y = zeros(length(y), yn);
for k = 1: yn
    Y(:, k) = (y == yu(k));
end
% ############################

% 按列归一化
for k = 1: size(X, 2)
    X(:, k) = (X(:, k) - mean(X(:, k))) / (max(X(:, k)) - min(X(:, k)));
end

Xtrain = [X(1: 40, :); X(51: 90, :); X(101:140, :)];
Ytrain = [Y(1: 40, :); Y(51: 90, :); Y(101: 140, :)];
Xtest = [X(41: 50, :); X(91: 100, :); X(141: 150, :)];
Ytest = [Y(41: 50, :); Y(91: 100, :); Y(141: 150, :)];

% 创建一个神经网络
% 隐藏层数为: hidden_layer 
% 连接方式为: 全连接
% 激活单元为: sigmoid
% 隐藏层单元数为: 输入层单元数
% 误差为: 均方误差
% 误差传递方式: 反向传播
% 优化算法: 梯度下降
% 数据读取方式: 每一行为一组数据
% 正则化项: l2

% 隐藏层
hiddenLayer = 2;
% 学习率, 其长度决定迭代次数
Alpha{1} = 10 * ones(500, 1);
Alpha{2} = 50: -0.1: 0.1;
% 正则化参数
lambda = 0.1;
% 训练误差
Jtrain = [];
% 测试误差
Jtest = [];

[W, P] = initWeight(Xtrain, Ytrain, hiddenLayer);
A = fp(Xtrain, W);

color = '.rgbk';
for ia = 1: length(Alpha)
    alpha = Alpha{ia};
    iter = length(alpha);
    for k = 1: iter
        P = bp(A, W, Ytrain, lambda);
        W = gradDesc(alpha(k), W, P);
        A = fp(Xtrain, W);
        Jtrain(k) = cost(A{hiddenLayer + 2}, Ytrain, W, lambda);
        B = fp(Xtest, W);
        Jtest(k) = cost(B{hiddenLayer + 2}, Ytest, W, lambda);
    end
    HatY = B{hiddenLayer + 2};
    % 显示结果, matlab 可以用 vec2ind
    [value, index] = max(HatY');
    disp(index);
    plot(Jtrain, color(ia * 2)); hold on; plot(Jtest, color(ia * 2 + 1)); 
end

legend({'train(static)', 'test(static)', 'train(dynamic)', 'test(dynamic)'});

code/matlab/run.m 执行结果: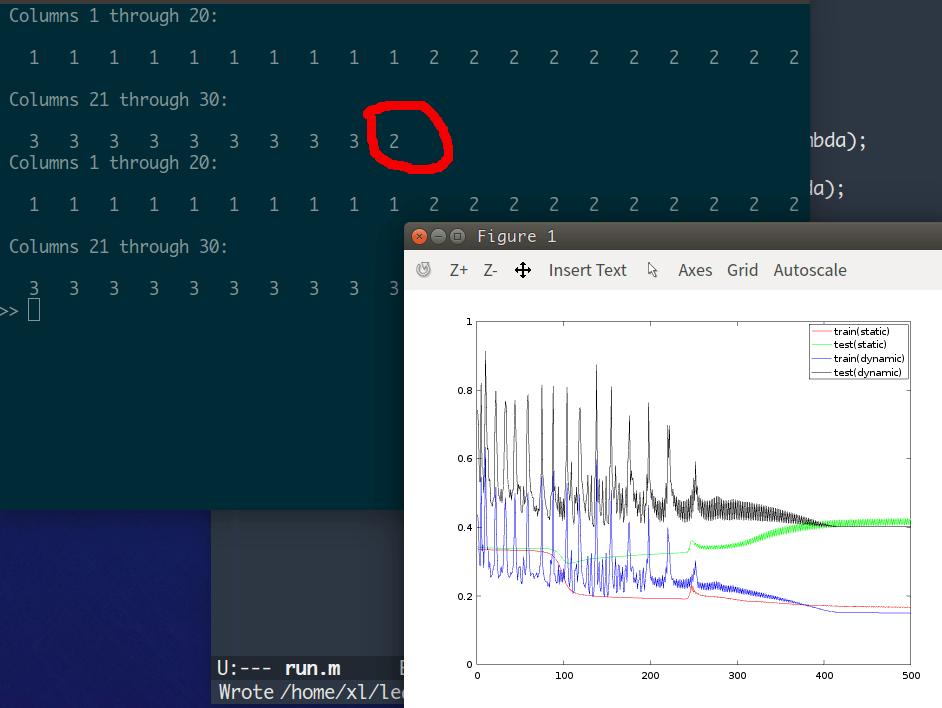
file

从上图可以看出，固定学习率为 10 的情况下，由于学习率稍大 (经测试 8 比较合适)，测试集的误差 (绿线) 有小幅波动。此时，即使对鸢尾花这个性质良好的数据分类，也有概率会出错。

在这个例子中，初始学习率若小于 1, 函数也会收敛 (局部最小值), 此时某一层的输出会全为 0, 之后的输出就没有意义了, 对应输出全为 1, 2, 3 中的一个。

最后

硬件实现

图3 所示网络只有加法单元, 乘法单元和 s 单元，都是最基础的数字电路原件，非常易于硬件实现，用 FPGA 实现也非常容易。

神经网络的变化

从图3 可以看出，神经网络的变化在于神经元的激活函数和连接方式，比如：

当激活函数使用卷积函数，构成卷积神经网络。
当连接中出现环路，构成递归神经网络，此时网络具有记忆，可以处理与顺序有关的问题。

改变求最优解的方式不算改变神经网络。

过拟合

可以证明 , 随着隐藏层的增加，神经网络可以以任意精度逼近任意连续函数。神经网络的问题在于，对样本的拟合能力太强，以至于不能很好的泛化到预测数据上。 matlab 中神经网络工具箱采用的做法是，将数据集随机分出一部分作为测试集，当训练集和测试集的误差都在减小则继续迭代，若训练集误差下降而测试集误差上升则停止迭代。

另外，每次训练随机去掉一些神经元，也有助于削弱过拟合。

初始化权重的方式对神经网络有很大的影响。

更多内容参考[1]。

附件下载

下载地址 ,选择附件: neuralNetwork.zip
文件说明

如果环境为 Windows 或 OS X, 有可能数据文件无法使用，执行 code/tools.py 生成数据再复制到代码所在目录即可
代码都是可以运行的，如果报错，请检查环境配置
code/matlab/SNN.m 是一个面向对象的神经网络实现，需要稍作修改才能在 octave 中运行，因为其中 logsig 和 vec2ind 函数是 matlab 才有的
如果公式里面的字看不清楚，可以查看附件里面的 nn.html ,这个是 js 渲染的，可以无限放大
如果用 PHP 实现向量化运算， math-php, php-ml 是两个现成的实现，但是它们的时间复杂度都是 O(n^3)。提供了一个用 php-cpp 封装 arma 作为 PHP 扩展的例子: linalgExtension, 时间复杂度大概是 O(n)。对比了几个 C 和 C++ 的库，arma 基本是最好用的了