监督学习基础概念

监督学习简介

给定一组数据点 \lbrace x^{(1)},…,x^{(m)}\rbrace 和与其对应的输出 {y^{(1)},…,y^{(m)}}，我们想要建立一个分类器，学习如何从 x 预测 y。

预测类型

不同类型的预测模型总结如下表：

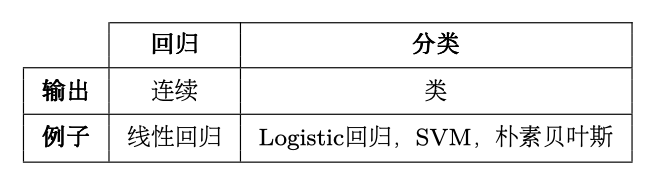
型号类型

不同型号总结如下表：

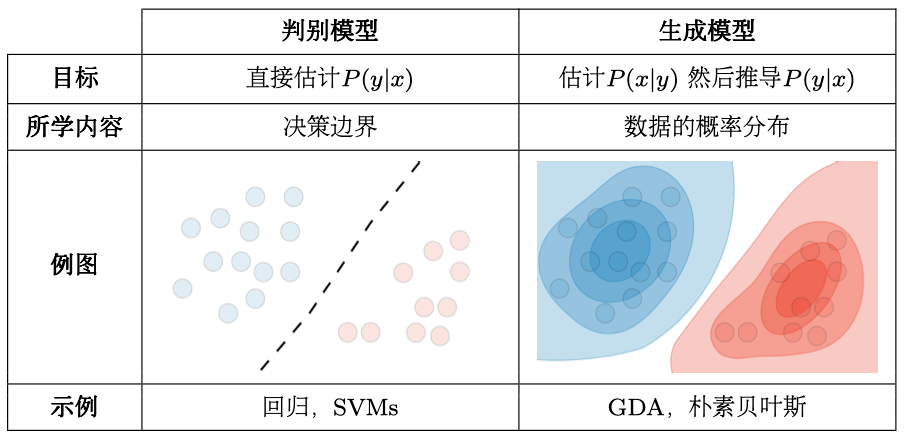
符号和一般概念

假设

假设我们选择的模型是h_\theta。对于给定的输入数据x^{(i)}，模型预测输出是h_\theta(x^{(i)})。

损失函数

损失函数是一个L:(z,y)\in \R \times Y \rightarrow L(z,y)\in \R的函数，其将真实数据值 y 和其预测值 z 作为输入，输出他们的不同程度。常见的损失函数总结如下表：

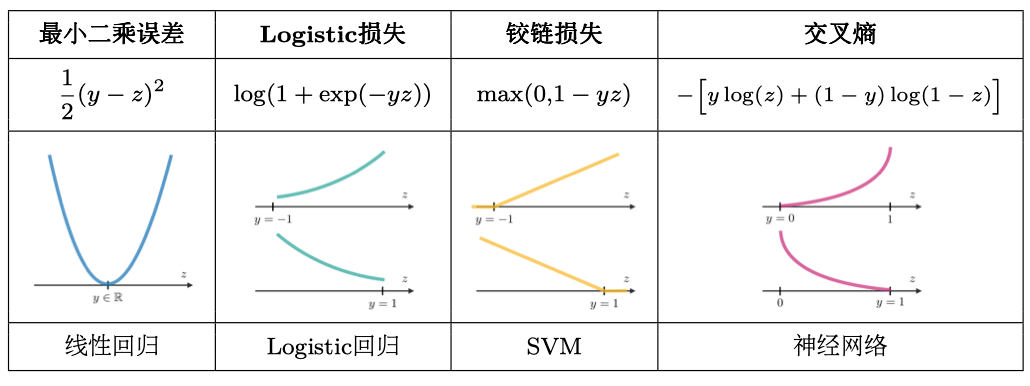
成本函数

成本函数J通常用于评估模型的性能，使用损失函数L定义如下：

J(\theta)=\sum\limits_{i=1}^mL(h_\theta(x^{(i)}),y^{(i)})

梯度下降

记学习率为\alpha\in \R，梯度下降的更新规则使用学习率和成本函数J，表示如下：

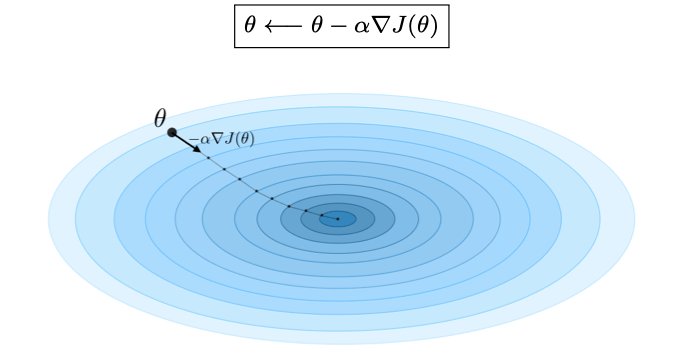
备注：随机梯度下降（SGD）是根据每个训练样本进行参数更新，而批量梯度下降是在一批训练样本 上进行更新。

似然

给定参数\theta的模型L(\theta)的似然性通过最大化似然性来找到最佳参数\theta。在实践中，我们使用更容易优化的对数似然l(\theta)=\log(L(\theta))。我们有：

\theta^{opt}=\arg \max L(\theta)

牛顿算法

牛顿算法是一种数值方法，目的是找到一个\theta使得l^\prime(\theta)=0，其更新规则如下：

\theta\leftarrow \theta - \frac{l^\prime(\theta)}{l^{\prime\prime}(\theta)}

备注：多维泛化，也称为Newton-Raphson 方法，具有以下更新规则：

\theta\leftarrow \theta - (\nabla_\theta^2l(\theta))^{-1}\nabla_\theta l(\theta)

本作品采用《CC 协议》，转载必须注明作者和本文链接