监督学习之支持向量机

支持向量机的目标是找到使决策界和训练样本之间最大化最小距离的线。

最优间隔分类器#

最有间隔分类器$h$ 是这样的：

$h(x)=sign(w^Tx-b)$

其中$(w,b)\in\R^n \times\R$ 是以下最优化问题的解决方案：

$\min\frac{1}{2}||w||^2$

使得

$y^{(i)}(w^Tx^{(i)}-b)\ge1$

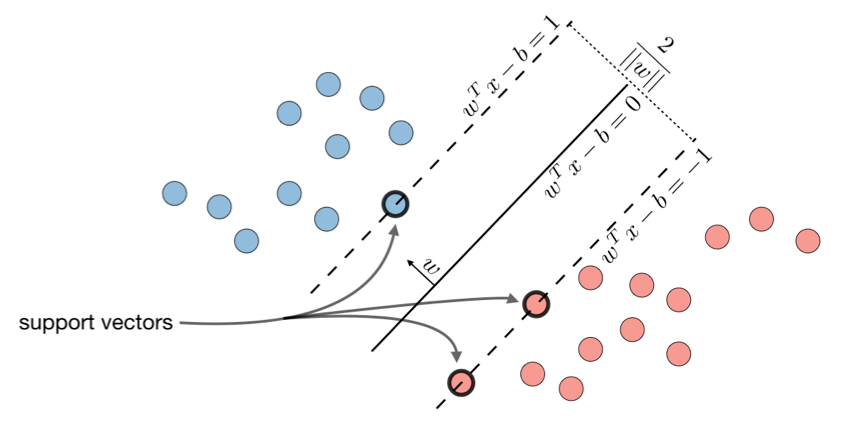
备注：该线定义为$w^Tx-b=0$

合页损失#

合页损失用于 SVM，定义如下：

$L(z,y)=[1-yz]_+=\max(0,1-yz)$

核#

给定特征映射$\phi$，我们定义核$K$ 为：

$K(x,z)=\phi(x)^T\phi(z)$

在实践中，由$K(x,z)=\exp(-\frac{||x-z||^2}{2\sigma^2})$ 定义的核$K$ 被称为高斯核，并且经常使用这种核。

备注：我们说我们使用「核技巧」来计算使用核的成本函数，因为我们实际上不需要知道显式映射$\phi$， 通常，这非常复杂。相反，只需要$K(x,z)$ 的值。

拉格朗日#

我们将拉格朗日$\mathcal{L}(w,b)$ 定义如下：

$\mathcal{L}(w,b)=f(w)+\sum\limits_{i=1}^l\beta_ih_i(w)$

备注：系数$\beta_i$ 被称为拉格朗日乘子

本作品采用《CC 协议》，转载必须注明作者和本文链接