循环神经网络

理论

Embedding 与 Padding

• Embedding 是把神经网络应用到 NLP 上的关键层，能够把词语转化成数字，从而让循环神经网络可以读取。
• 序列式问题
• 循环神经网络
• LSTM 模型

  Embedding

  One-hot 编码
• Word -> index -> [0, 0, 0, …, 0, 1, 0, …, 0]
  Dense embedding
• Word -> index -> [1.2, 4.2, 2.9, …, 0.1]

  Padding

• Word index: [3,2,5,9,1]
• padding: [3,2,5,9,1,0,0,0,0,0]

  0: unknow word（UNK）
  如果位数不足，用「padding」，如果位数溢出，用「截断」。

合并

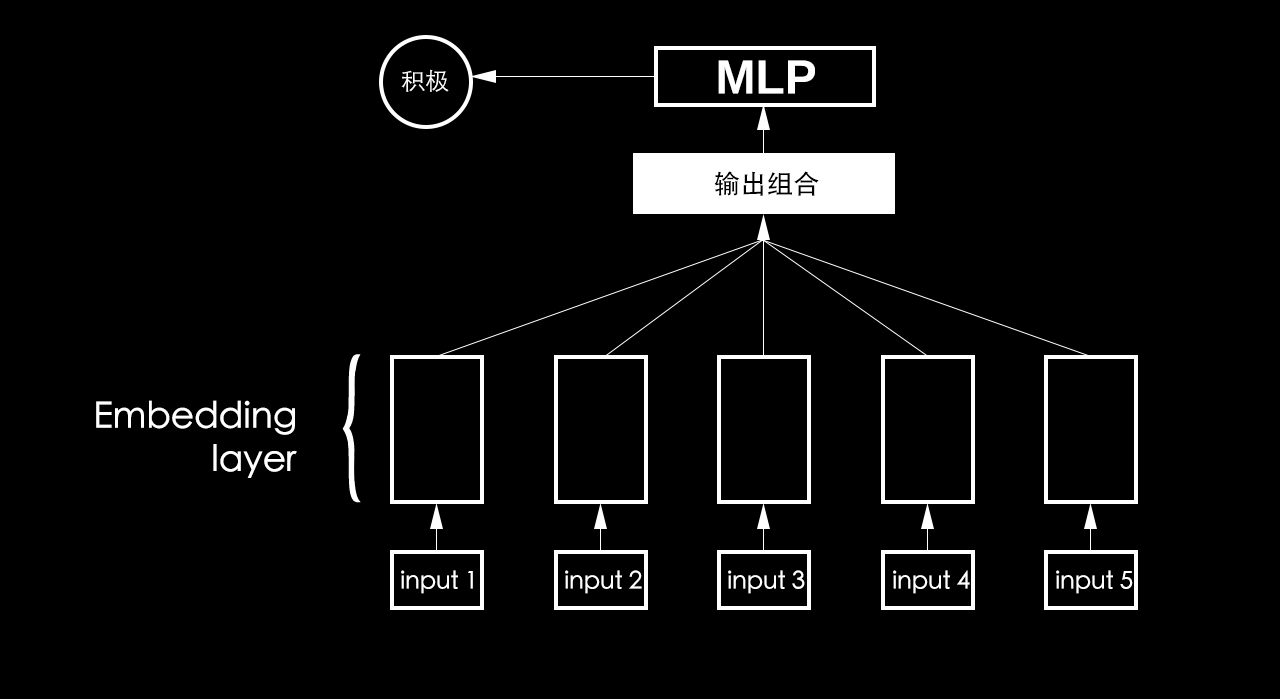
合并 + padding 的缺点

合并 + padding 的操作会使信息丢失，比如多个 embedding 合并，会产生 Pad 噪音，无主次。这样做会有太多的无效计算，非常抵消，因为有太多的 padding。

序列式问题

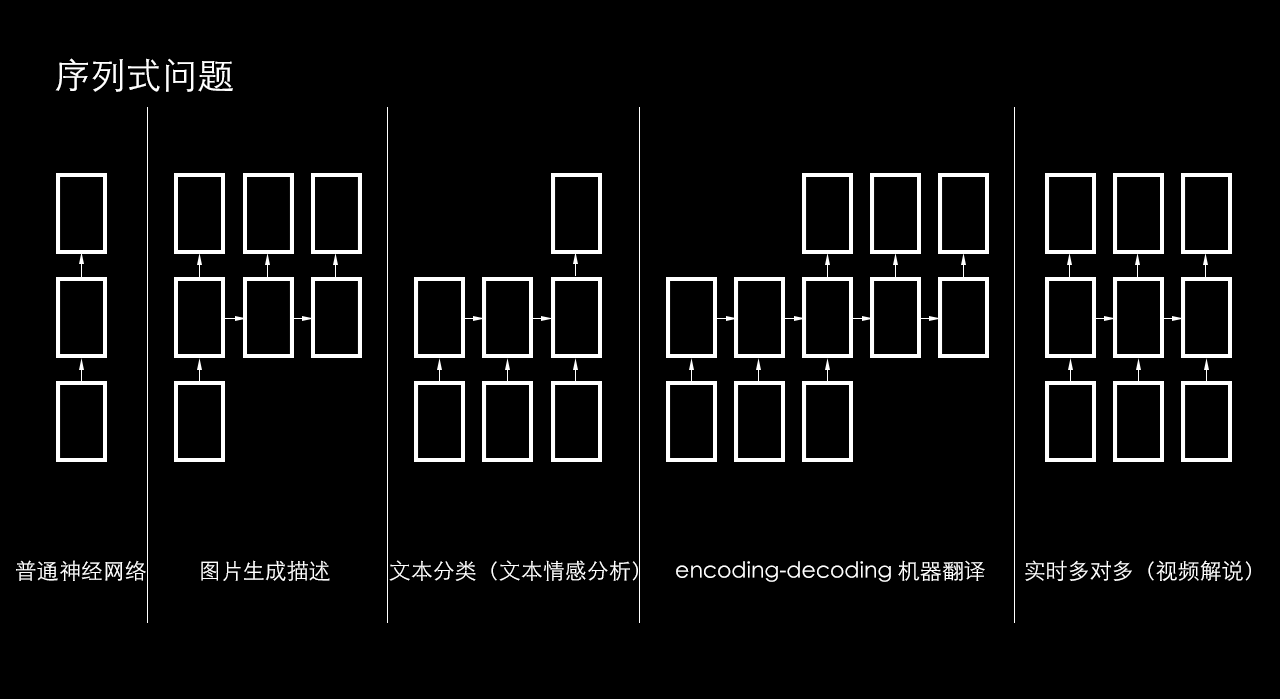
循环神经网络

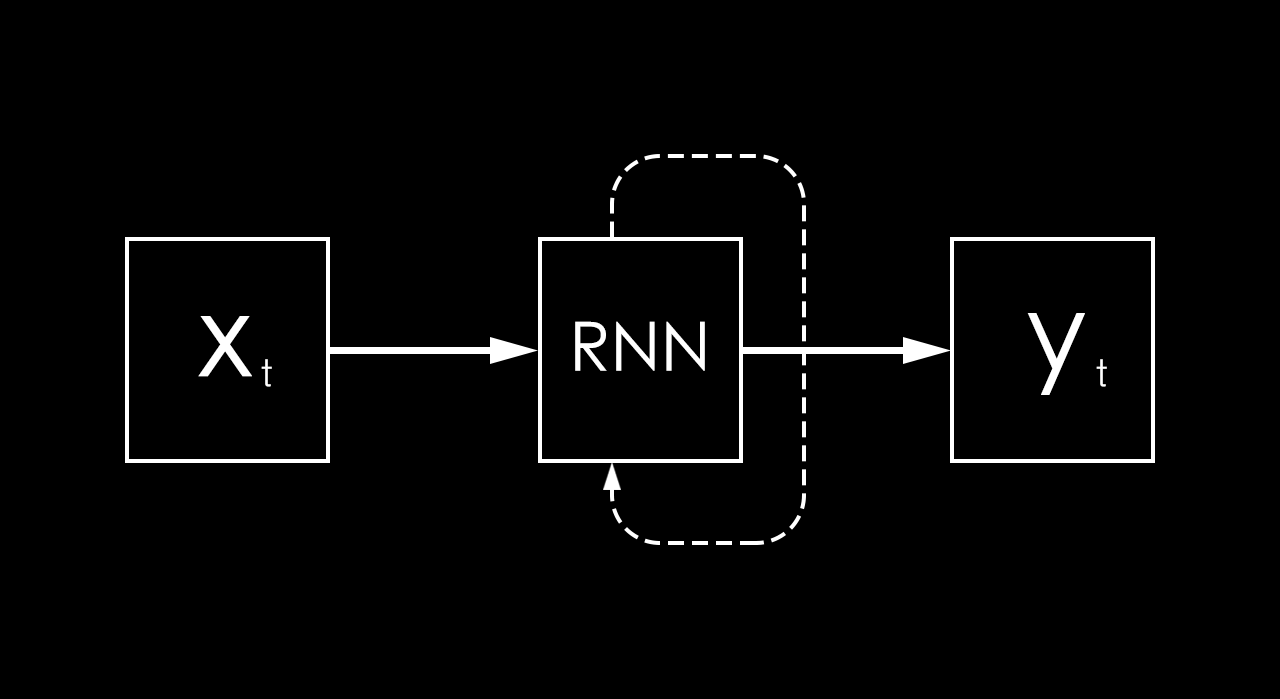
上图中虚线的作用是维护一个状态作为下一步的额外输入，每一步使用同样的激活函数和参数。

s_t=f_W(s_{t-1},x_t)

s_t代表新状态，s_{t-1}代表旧状态，x_t代表输入，f_W代表「RNN」的计算函数。

s_t=f_W(s_{t-1},x_t)\\{}\\ \downarrow\\{}\\ s_t=\tanh(Ws_{t-1}+Ux_t)\\{}\\ \widehat{y_t}=\mathrm{softmax}(Vs_t)

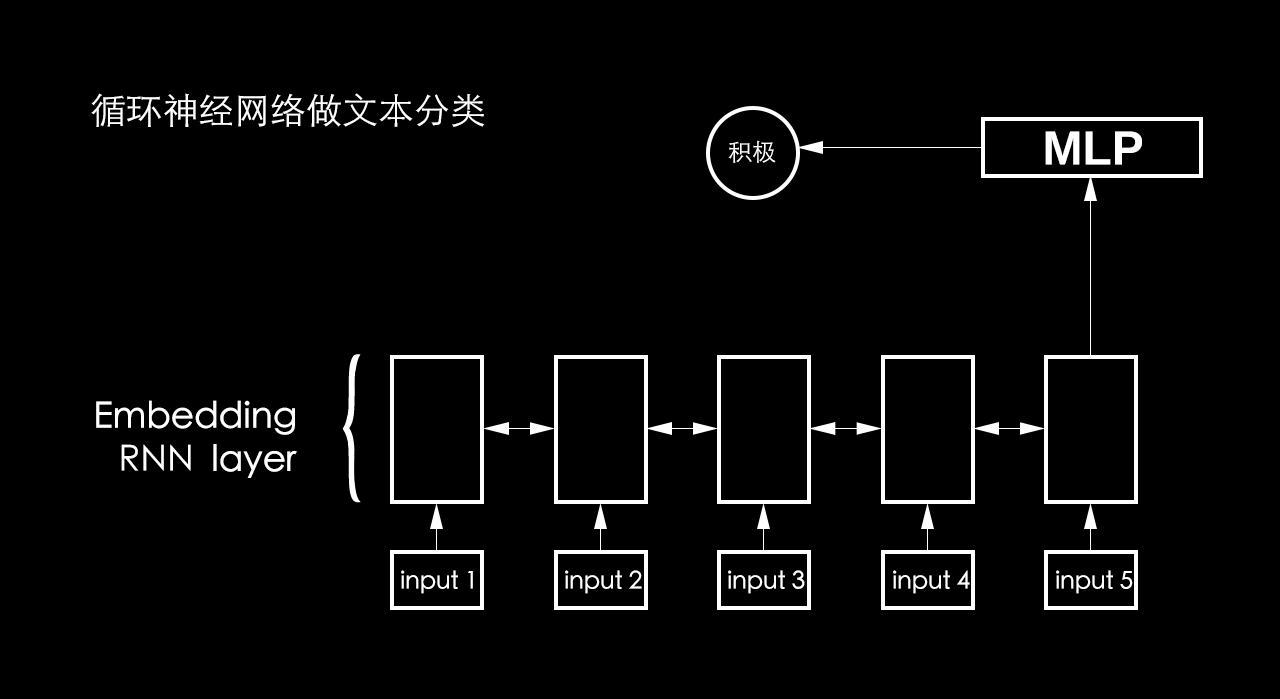
传统文本处理任务的方法中一般将 TF-IDF 向量作为特征输入。显而易见，这样的表示实际上丢失了输入的文本序列中每个单词的顺序。在神经网络的建模过程中，一般的前馈神经网络，如卷积神经网络，通常接受一个定长的向量作为输入。卷积神经网络对文本数据建模时，输入变长的字符串或者单词串，然后通过滑动窗口加池化的方式将原先的输入转换成一个固定长度的向量表示，这样做可以捕捉到原文本中的一些局部特征，但是两个单词之间的长距离依赖关系还是很难被学习到。
循环神经网络却能很好地处理文本数据变长并且有序的输入序列。它模拟了人阅读一篇文章的顺序，从前到后阅读文章中的每一个单词，将前面阅读到的有用信息编码到状态变量中去，从而拥有了一定的记忆能力，可以更好地理解之后的文本。
其网络结构如下图所示：

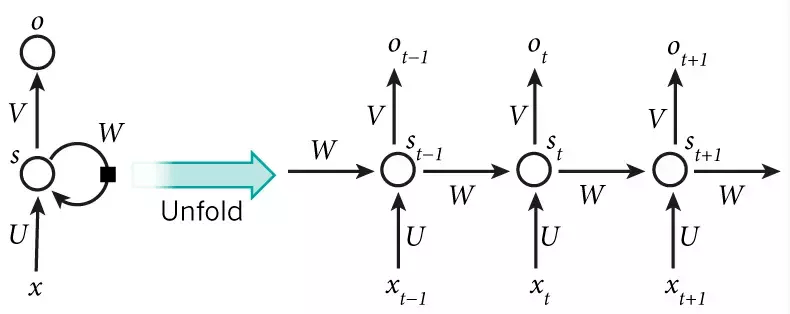
由图可见，t是时刻，x是输入层，s是隐藏层，o是输出层，矩阵W就是隐藏层上一次的值作为这一次的输入的权重。
输出层o和隐藏层s的计算方法：

\displaystyle o_t=g(Vs_t)\\{}\\ s_t=f(Ux_t+Ws_{t-1})

可以连续查看o_t迭代关系：

\displaystyle o_t=g(Vs_t)\\{}\\ =Vf(Ux_t+Ws_{t-1})\\{}\\ =Vf(Ux_t+Wf(Ux_{t-1}+Ws_{t-2}))\\{}\\ =Vf(Ux_t+Wf(Ux_{t-1}+Wf(Ux_{t-2}+Ws_{t-3})))\\{}\\ =Vf(Ux_t+Wf(Ux_{t-1}+Wf(Ux_{t-2}+Wf(Ux_{t-3}+...))))

其中f和g为激活函数，U为输入层到隐含层的权重矩阵，W为隐含层从上一时刻到下一时刻状态转移的权重矩阵。在文本分类任务中，f可以选取\tanh函数或者\mathrm{ReLU}函数，g可以采用\mathrm{Softmax}函数。

通过最小化损失误差（即输出的y与真实类别之间的距离），我们可以不断训练网络，使得得到的循环神经网络可以准确地预测文本所属的类别，达到分类目的。相比于卷积神经网络等前馈神经网络，循环神经网络由于具备对序列顺序信息的刻画能力，往往能得到更准确的结果。

训练算法

RNN 的训练算法为：BPTT
BPTT 的基本原理和 BP 算法是一样的，同样是三步：
1.前向计算每个神经元的输出值；
2.反向计算每个神经元的误差项值，它是误差函数E对神经元j的加权输入的偏导数；
3.计算每个权重的梯度。
最后再用随机梯度下降算法更新权重。
具体参考：详解循环神经网络(Recurrent Neural Network)
最后由链式法则得到下面以雅可比矩阵来表达的每个权重的梯度：

\displaystyle 循环层权重矩阵W的梯度的公式\\{}\\ \nabla _WE=\sum_{i=1}^t\nabla _W {_{_i}}E\\{}\\ =\left [\begin{matrix} \delta_1^ts_1^{t-1} & \delta_1^ts_2^{t-1} & \cdots & \delta_1^ts_n^{t-1}\\{}\\ \delta_2^ts_1^{t-1} & \delta_2^ts_2^{t-1} & \cdots & \delta_2^ts_n^{t-1}\\{}\\ \vdots & \vdots & \ddots & \vdots\\{}\\ \delta_n^ts_1^{t-1} & \delta_n^ts_2^{t-1} & \cdots & \delta_n^ts_n^{t-1} \end{matrix} \right] +\cdots+\left [\begin{matrix} \delta_1^1s_1^0 & \delta_1^1s_2^0 & \cdots & \delta_1^1s_n^0\\{}\\ \delta_2^1s_1^0 & \delta_2^1s_2^0 & \cdots & \delta_2^1s_n^0\\{}\\ \vdots & \vdots & \ddots & \vdots\\{}\\ \delta_n^1s_1^0 & \delta_n^1s_2^0 & \cdots & \delta_n^1s_n^0 \end{matrix} \right]\\{}\\ 循环层权重矩阵U的梯度的公式\\{}\\ \nabla_U{_{_t}}E=\left[ \begin{matrix} \delta_1^tx_1^t & \delta_1^tx_2^t & \cdots & \delta_1^tx_m^t\\{}\\ \delta_2^tx_1^t & \delta_2^tx_2^t & \cdots & \delta_2^tx_m^t\\{}\\ \vdots & \vdots & \ddots & \vdots\\{}\\ \delta_n^tx_1^t & \delta_n^tx_2^t & \cdots & \delta_n^tx_m^t \end{matrix} \right]

由于预测的误差是沿着神经网络的每一层反向传播的，因此当雅克比矩阵的最大特征值大于1时，随着离输出越来越远，每层的梯度大小会呈指数增长，导致梯度爆炸；反之，若雅克比矩阵的最大特征值小于1，梯度的大小会呈指数缩小，产生梯度消失。对于普通的前馈网络来说，梯度消失意味着无法通过加深网络层次来改善神经网络的预测效果，因为无论如何加深网络，只有靠近输出的若干层才真正起到学习的作用。这使得循环神经网络模型很难学习到输入序列中的长距离依赖关系。
RNN梯度下降的详细推导

梯度爆炸的问题可以通过梯度裁剪来缓解，即当梯度的范式大于某个给定值时，对梯度进行等比收缩。而梯度消失问题相对比较棘手，需要对模型本身进行改进。深度残差网络是对前馈神经网络的改进，通过残差学习的方式缓解了梯度消失的现象，从而使得我们能够学习到更深层的网络表示；而对于循环神经网络来说，长短时记忆模型及其变种门控循环单元等模型通过加入门控机制，很大程度上弥补了梯度消失所带来的损失。

在英文里递归神经网络（recursive neural network）和循环神经网络（recurrent neural net work）都简称 RNN，雪上加霜的是，有些地方把 recurrent neural network 翻译成递归伸进网络，或者，时间递归神经网络。
一般提到的 RNN 指的是 recurrent neural network，也就是循环神经网络。

本作品采用《CC 协议》，转载必须注明作者和本文链接