数据结构与算法整理总结---图

如何理解“图”？

和树⽐起来，这是⼀种更加复杂的⾮线性表结构。

我们知道，树中的元素我们称为节点，图中的元素我们就叫作顶点（vertex）。从我画的图中可以看出来，图中的⼀个顶点可以与任意其他顶点建⽴连接关系。我们把这种建⽴的关系叫作边（edge）。

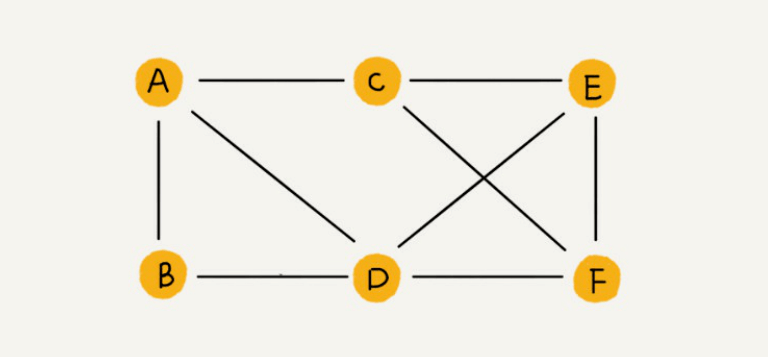
我们⽣活中就有很多符合图这种结构的例⼦。就拿微信举例⼦吧。我们可以把每个⽤户看作⼀个顶点。如果两个⽤户之间互加好友，那就在两者之间建⽴⼀条边。所以，整个微信的好友关系就可以⽤⼀张图来表示。其中，每个⽤户有多少个好友，对应到图中，就叫作顶点的度（degree），就是跟顶点相连接的边的条数。

实际上，微博的社交关系跟微信还有点不⼀样，或者说更加复杂⼀点。微博允许单向关注，也就是说，⽤户A关注了⽤户B，但⽤户B可以不关注⽤户A。那我们如何⽤图来表示这种单向的社交关系呢？

我们可以把刚刚讲的图结构稍微改造⼀下，引⼊边的“⽅向”的概念。

如果⽤户A关注了⽤户B，我们就在图中画⼀条从A到B的带箭头的边，来表示边的⽅向。如果⽤户A和⽤户B互相关注了，那我们就画⼀条从A指向B的边，再画⼀条从B指向A的边。我们把这种边有⽅向的图叫作“有向图”。以此类推，我们把边没有⽅向的图就叫作“⽆向图”。

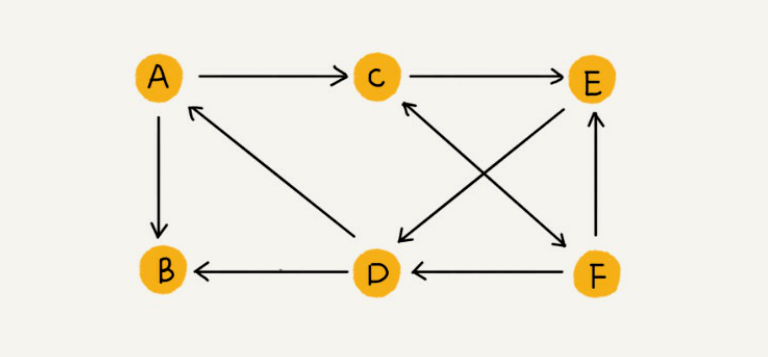
⽆向图中有“度”这个概念，表示⼀个顶点有多少条边。在有向图中，我们把度分为⼊度（In-degree）和出度（Out-degree）。

顶点的⼊度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例⼦，⼊度就表示有多少粉丝，出度就表示关注了多少⼈。

QQ中的社交关系要更复杂的⼀点。不知道你有没有留意过QQ亲密度这样⼀个功能。QQ不仅记录了⽤户之间的好友关系，还记录了两个⽤户之间的亲密度，如果两个⽤户经常往来，那亲密度就⽐较⾼；如果不经常往来，亲密度就⽐较低。如何在图中记录这种好友关系的亲密度呢？

这⾥就要⽤到另⼀种图，带权图（weighted graph）。在带权图中，每条边都有⼀个权重（weight），我们可以通过这个权重来表示QQ好友间的亲密度。

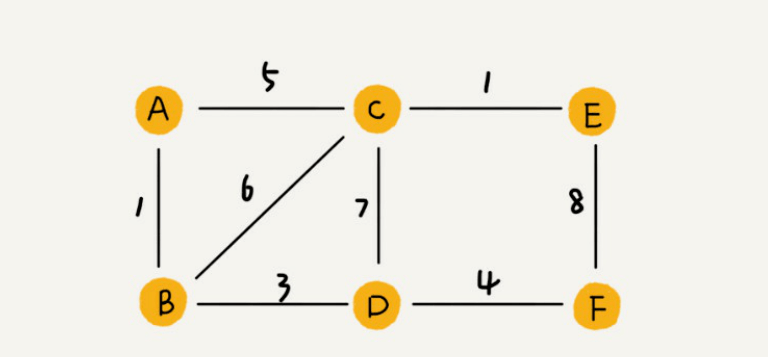
邻接矩阵存储⽅法

图最直观的⼀种存储⽅法就是，邻接矩阵（Adjacency Matrix）。

邻接矩阵的底层依赖⼀个⼆维数组。对于⽆向图来说，如果顶点i与顶点j之间有边，我们就将A[i][j]和A[j][i]标记为1；对于有向图来说，如果顶点i到顶点j之间，有⼀条箭头从顶点i指向顶点j的边，那我们就将A[i][j]标记为1。同理，如果有⼀条箭头从顶点j指向顶点i的边，我们就将A[j][i]标记为1。对于带权图，数组中就存储相应的权重。

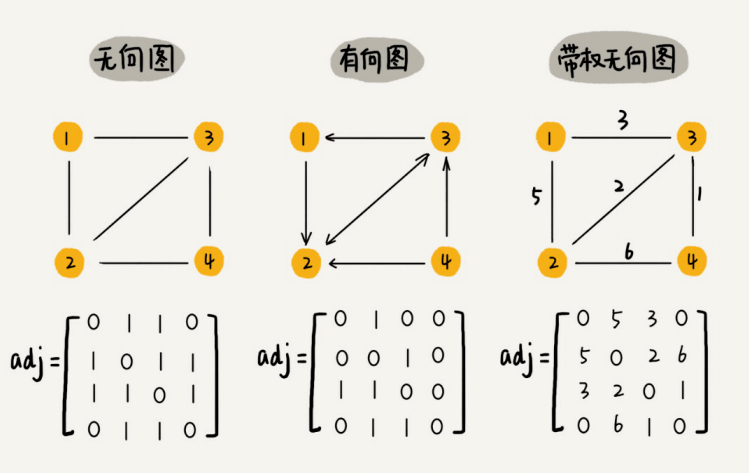
⽤邻接矩阵来表示⼀个图，虽然简单、直观，但是⽐较浪费存储空间。为什么这么说呢？

对于⽆向图来说，如果A[i][j]等于1，那A[j][i]也肯定等于1。实际上，我们只需要存储⼀个就可以了。也就是说，⽆向图的⼆维数组中，如果我们将其⽤对⻆线划分为上下两部分，那我们只需要利⽤上⾯或者下⾯这样⼀半的空间就⾜够了，另外⼀半⽩⽩浪费掉了。

还有，如果我们存储的是稀疏图（Sparse Matrix），也就是说，顶点很多，但每个顶点的边并不多，那邻接矩阵的存储⽅法就更加浪费空间了。⽐如微信有好⼏亿的⽤户，对应到图上就是好⼏亿的顶点。但是每个⽤户的好友并不会很多，⼀般也就三五百个⽽已。如果我们⽤邻接矩阵来存储，那绝⼤部分的存储空间都被浪费了。

但这也并不是说，邻接矩阵的存储⽅法就完全没有优点。⾸先，邻接矩阵的存储⽅式简单、直接，因为基于数组，所以在获取两个顶点的关系时，就⾮常⾼效。其次，⽤邻接矩阵存储图的另外⼀个好处是⽅便计算。这是因为，⽤邻接矩阵的⽅式存储图，可以将很多图的运算转换成矩阵之间的运算。⽐如求解最短路径问题时会提到⼀个Floyd-Warshall算法，就是利⽤矩阵循环相乘若⼲次得到结果。

邻接表存储⽅法

针对上⾯邻接矩阵⽐较浪费内存空间的问题，我们来看另外⼀种图的存储⽅法，邻接表（Adjacency List）。

乍⼀看，邻接表是不是有点像散列表？每个顶点对应⼀条链表，链表中存储的是与这个顶点相连接的其他顶点。另外我需要说明⼀下，图中画的是⼀个有向图的邻接表存储⽅式，每个顶点对应的链表⾥⾯，存储的是指向的顶点。对于⽆向图来说，也是类似的，不过，每个顶点的链表中存储的，是跟这个顶点有边相连的顶点。

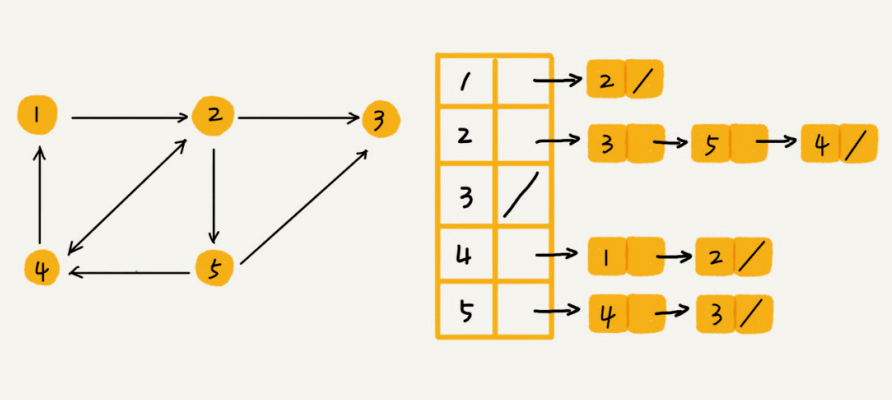
邻接矩阵存储起来⽐较浪费空间，但是使⽤起来⽐较节省时间。相反，邻接表存储起来⽐较节省空间，但是使⽤起来就⽐较耗时间。

就像图中的例⼦，如果我们要确定，是否存在⼀条从顶点2到顶点4的边，那我们就要遍历顶点2对应的那条链表，看链表中是否存在顶点4。⽽且，我们前⾯也讲过，链表的存储⽅式对缓存不友好。所以，⽐起邻接矩阵的存储⽅式，在邻接表中查询两个顶点之间的关系就没那么⾼效了。

本作品采用《CC 协议》，转载必须注明作者和本文链接