深入理解数据结构--二叉树（进阶篇1）

在上篇整理了二叉树的相对基础的信息深入理解数据结构–二叉树（基础篇）

接下来深入讲解二叉树的进阶内容

二叉查找树

二叉查找树(Binary Search Tree)，顾名思义，是用来查找数据的。它在二叉树的基础上，增加了几个规则：

1. 如果左子树不为空，则左子树上所有节点的值均小于根节点的值。
2. 如果右子树不为空，则右子树上所有节点的值均大于根节点的值。
3. 左、右子树也都是二叉查找树。

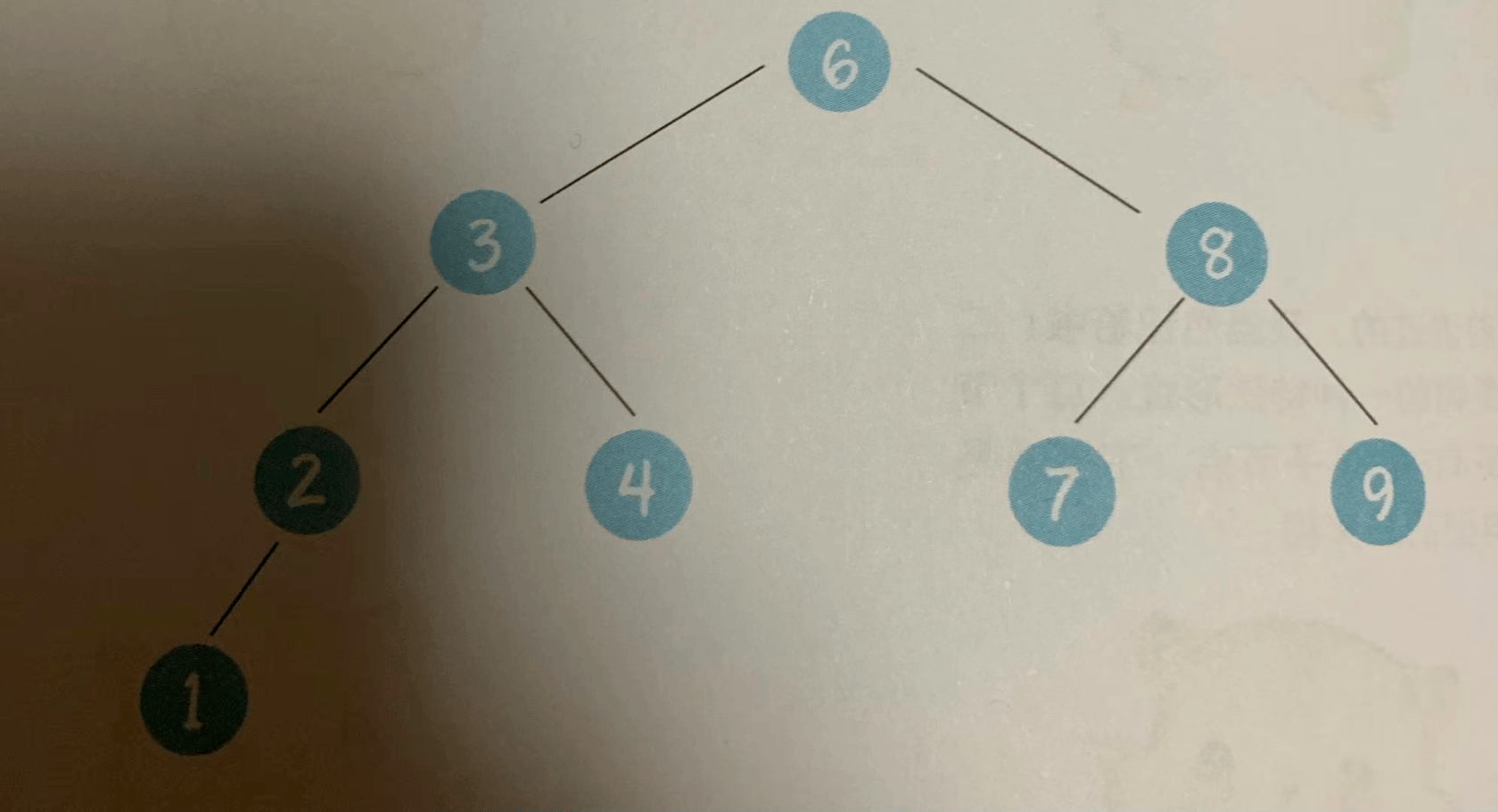
下图就是一颗标准的二叉查找树：

二叉树的代码结构用go的结构体来实现如下：

type binaryTree struct {
    value int
    leftNode *binaryTree
    rightNode *binaryTree
}

二叉查找树有三个操作：查找、插入和删除

二叉树的查找

假设我们要查找的值是4，查找过程如下：

1. 访问根节点6，发现4<6

2. 访问根节点6的左孩子节点3，发现4>3

3. 访问节点3的右孩子节点4，发现正是要查找的节点

对于一个节点分布相对平衡的二叉查找树，如果节点总数是n，那么查找节点的时间复杂度就是O(logn)，和树的深度成正比

实现代码如下：

//节点查找
func findNode(num int,tree *binaryTree) bool{
    targetNode := tree
    for targetNode != nil{
        if targetNode.value == num {
            return true
        }else if targetNode.value > num {
            targetNode = targetNode.leftNode
        }else {
            targetNode = targetNode.rightNode
        }
    }
    return false
}

二叉树的插入

二叉树的插入遍历过程与查找类似，这里就直接写代码实现

//节点插入
func insertNode(tree *binaryTree,node *binaryTree) *binaryTree {

    if tree.value == 0 {
        return node
    }
    if tree.value == node.value {
        return tree
    }else if tree.value > node.value {
        //往左子树走,为空则直接插入节点
        if tree.leftNode == nil {
            tree.leftNode = node
        }else {
            tree.leftNode = insertNode(tree.leftNode,node)
        }
    }else {
        //往右子树走,为空则直接插入节点
        if tree.rightNode == nil {
            tree.rightNode = node
        }else {
            tree.rightNode = insertNode(tree.rightNode,node)
        }
    }
    return tree
}

二叉树的删除

相对查找和插入，二叉树的删除过程相对复杂一些，代码实现上也有对应的逻辑

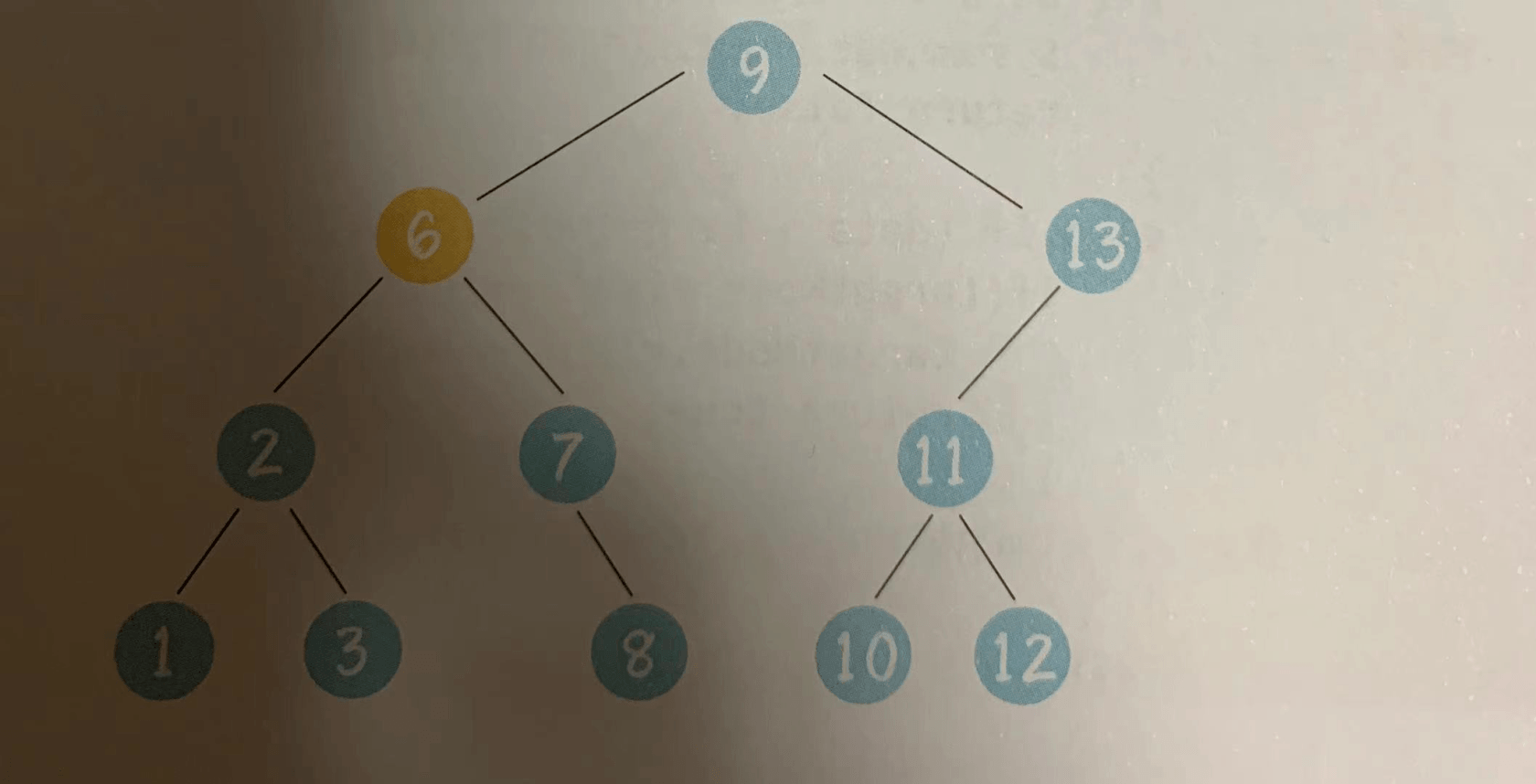
二叉树的删除操作，可分为三种情况：

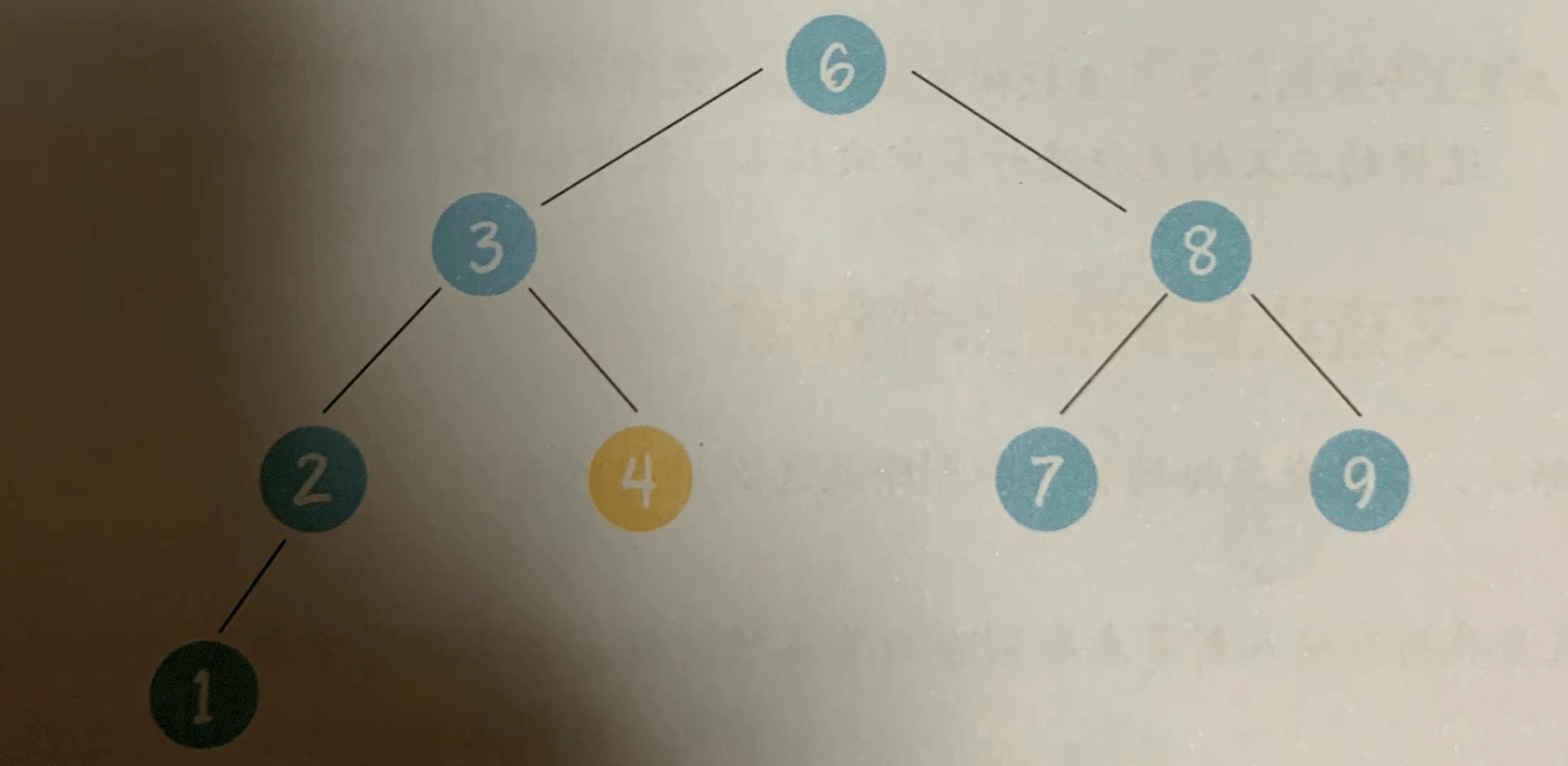
情况1，待删除的节点没有子节点

上图中，待删除的节点12是叶子节点，没有孩子，因此直接删除即可

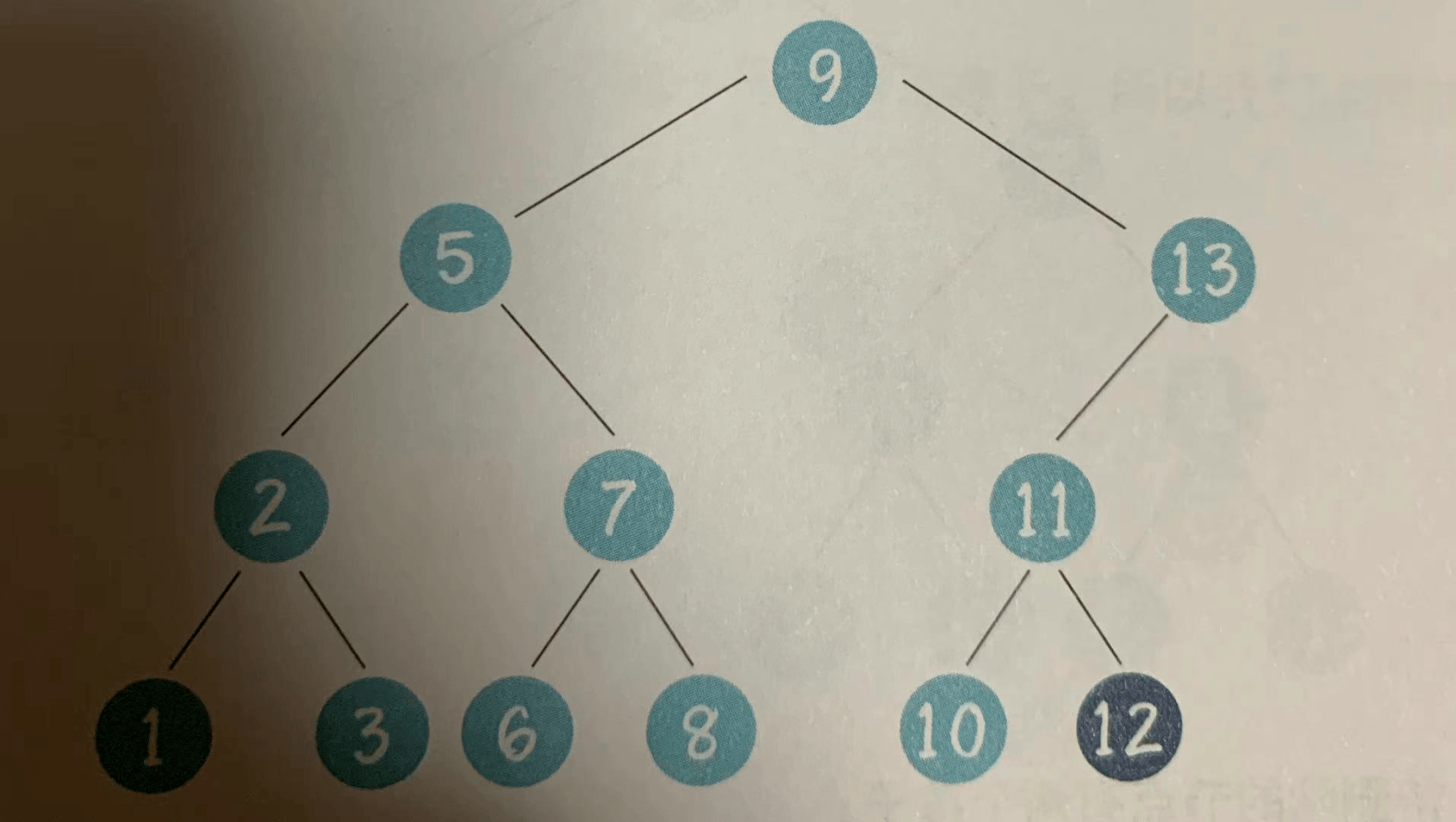
情况2，待删除的节点有一个孩子

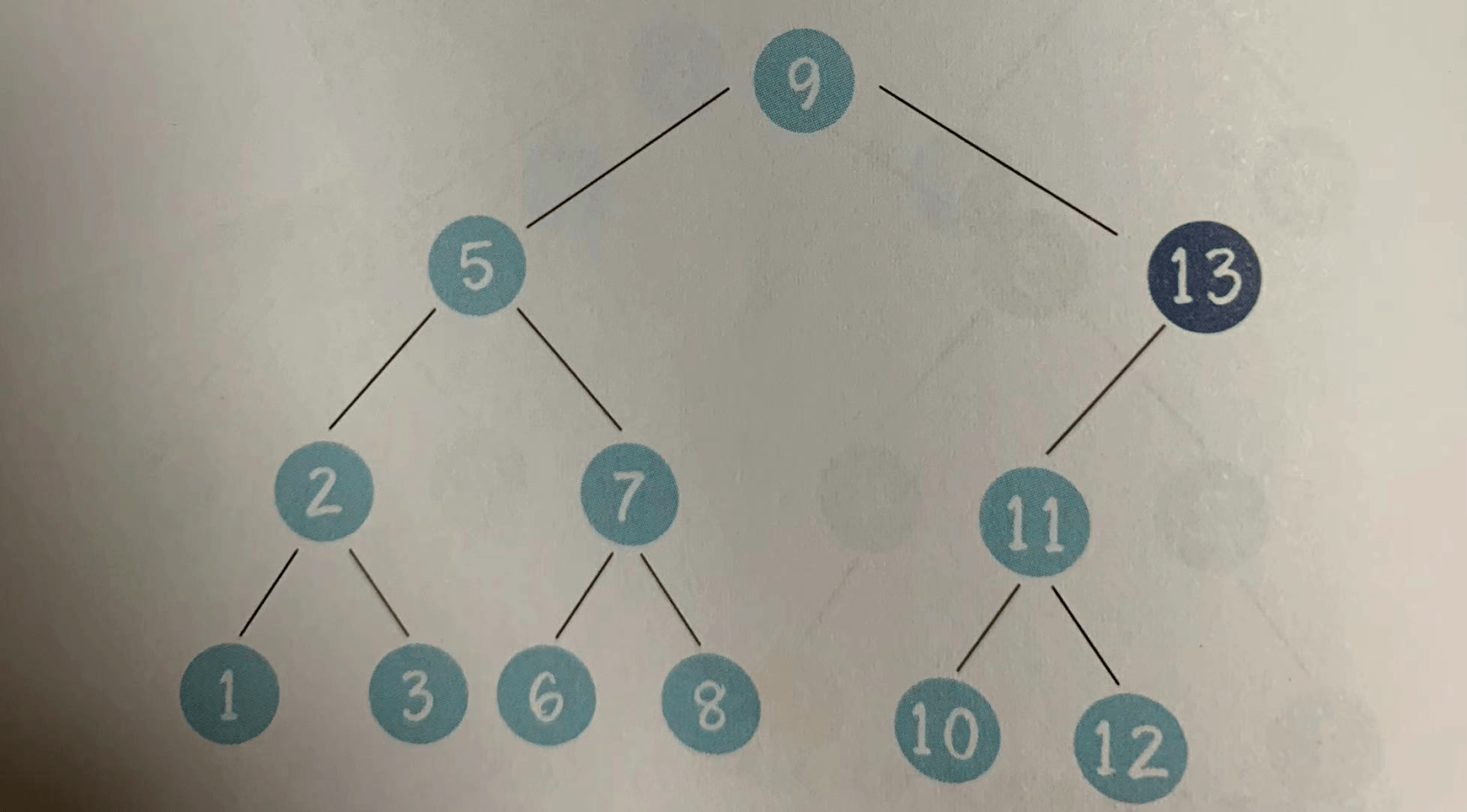
上图中，待删除的节点13只有左孩子，于是我们让左孩子节点11取代被删除的节点，节点11以下的节点关系无须变动

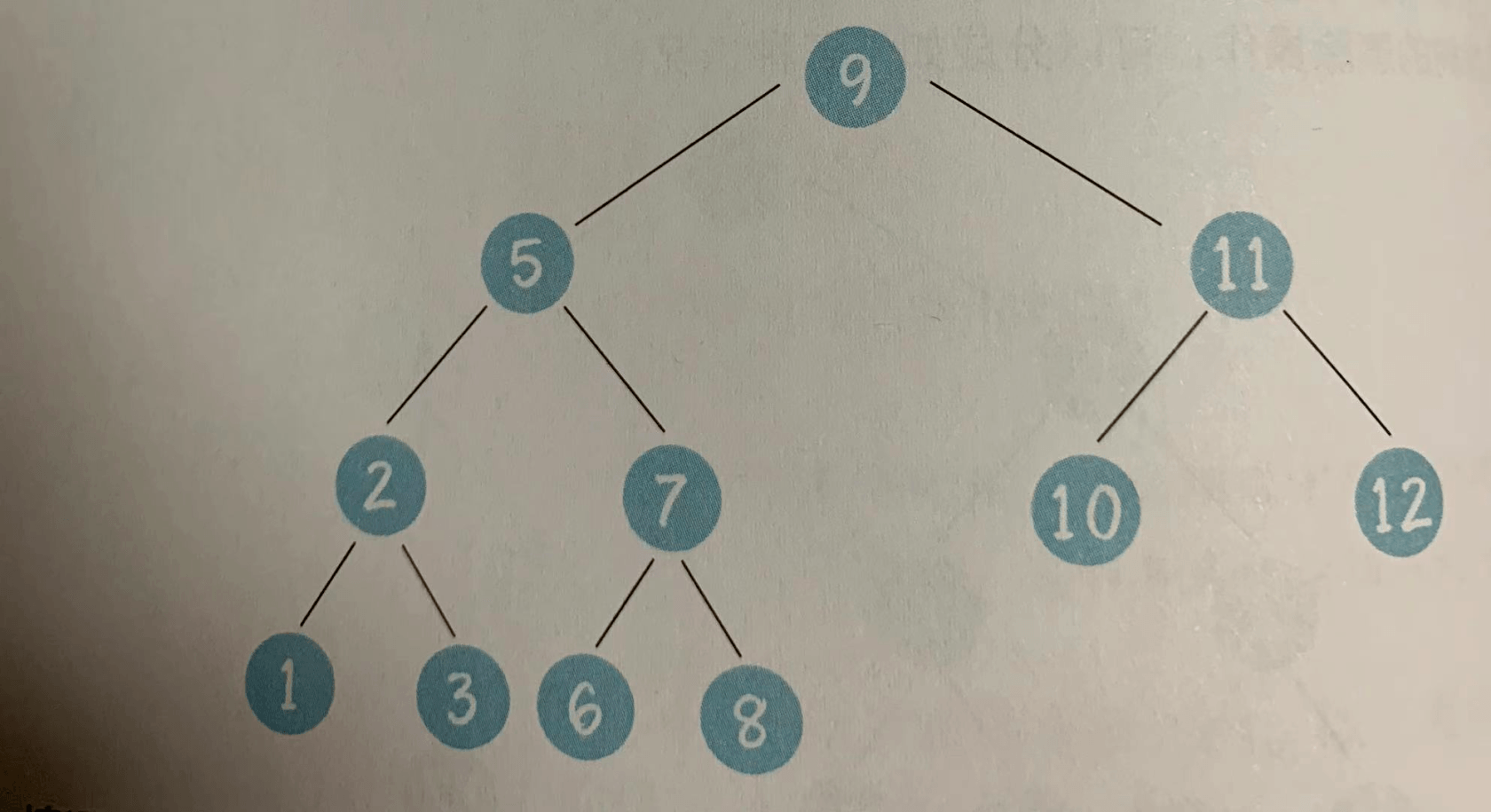
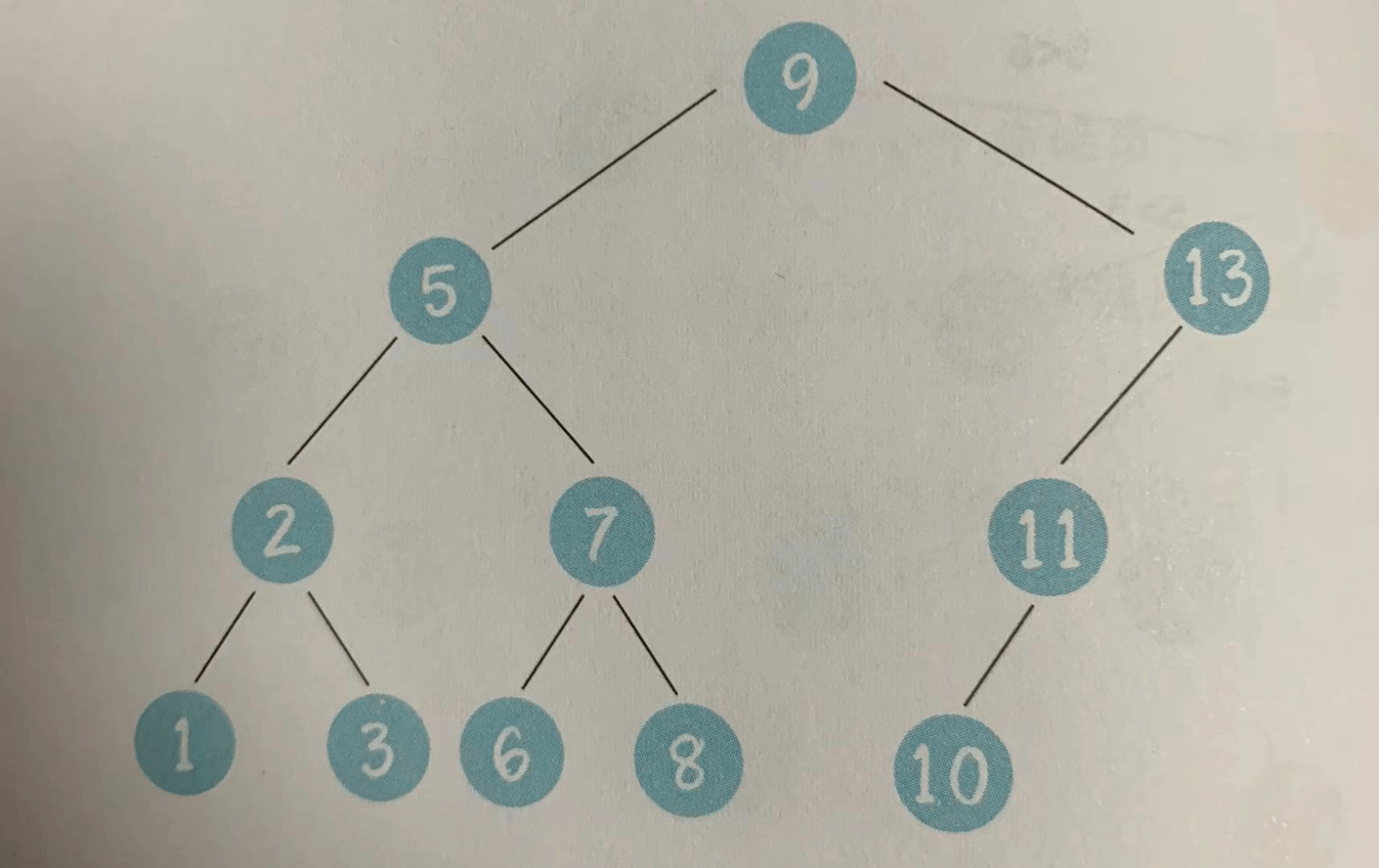
情况3，待删除的节点有两个孩子

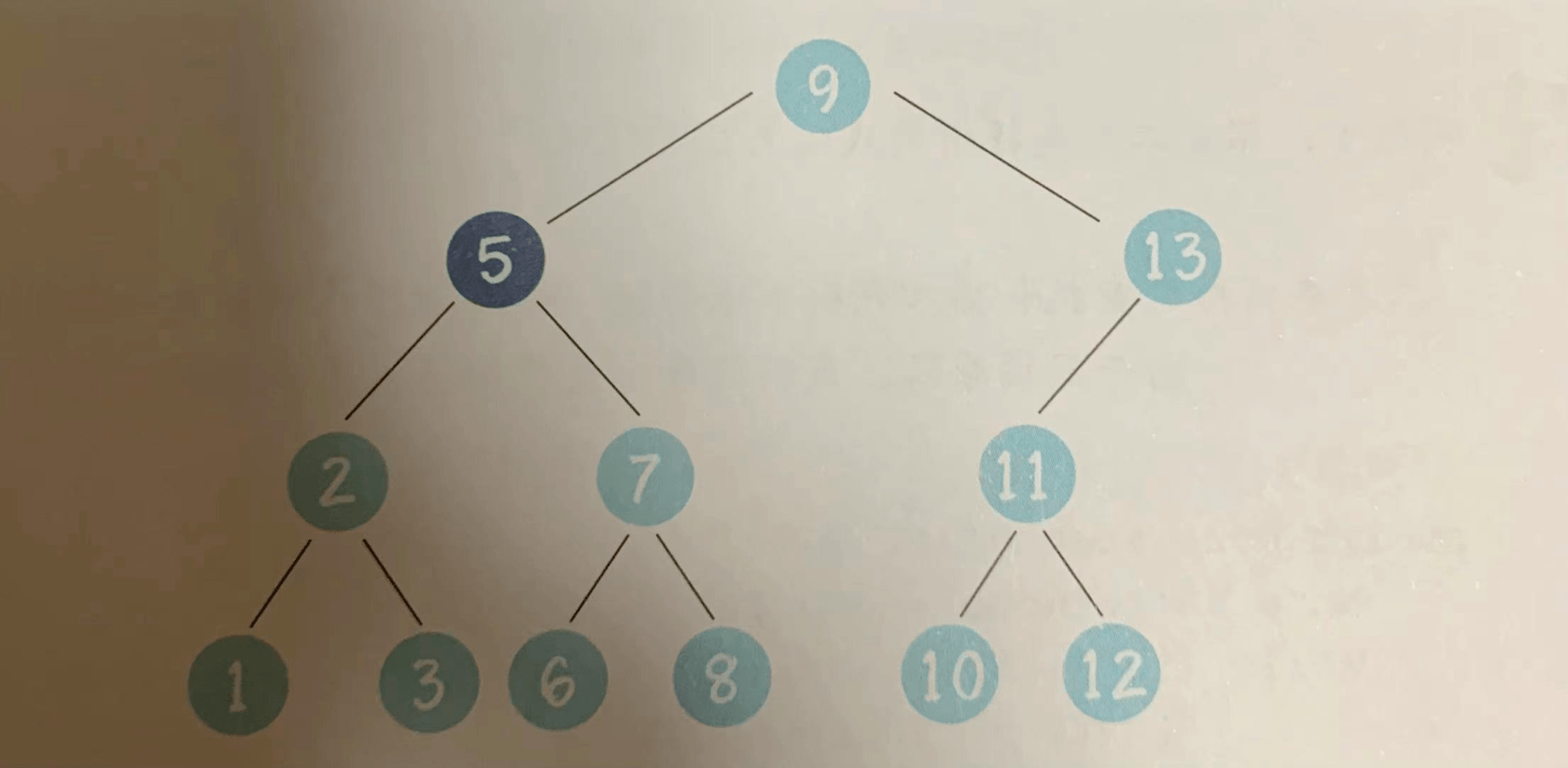
上图中，待删除的节点5有两个孩子，这种情况比较复杂。需要选择与待删除节点最接近的节点来取代它。

上面的例子中，节点3仅小于节点5，节点6仅大于节点5.两者都是合适的选择。但习惯上我们选择仅大于待删除节点的节点，也就是用节点6来取代它。

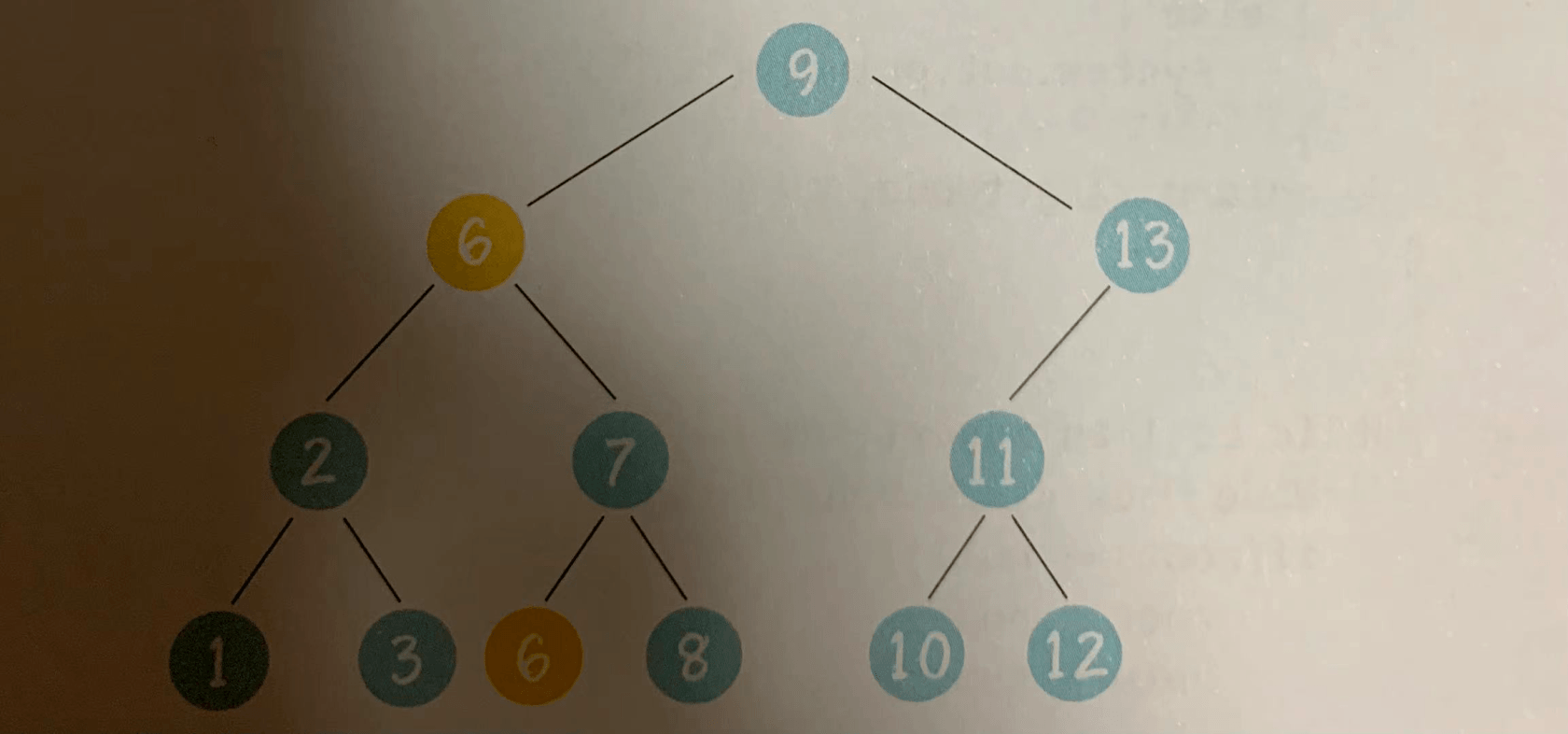
被选中的节点6，仅大于节点5，因此一定没有左孩子。所以我们按照情况1或情况2的方式，删除多余的节点6。

代码实现如下，实现上相对复杂一点，需要运用递归的方式去处理：

//删除节点
func deleteNode(num int,tree *binaryTree) *binaryTree{
   //先查看删除的值是否存在树当中
  find := findNode(num,tree)
   if find {
      //配置到节点值，执行删除操作
  if tree.value == num {
         //删除的节点无左右节点
  if tree.leftNode == nil && tree.rightNode == nil {
            tree = &binaryTree{}
         }else if tree.leftNode == nil && tree.rightNode != nil {
            //左节点为空，右节点不为空
  tree = tree.rightNode
         }else if tree.rightNode == nil && tree.leftNode != nil {
            //右节点为空，左节点不为空
  tree = tree.leftNode
         }else{
            //节点左右节点都存在
  tree = replaceNode(tree)
         }
      }else if tree.value > num {
         tree.leftNode = deleteNode(num,tree.leftNode)
      }else {
         tree.rightNode = deleteNode(num,tree.rightNode)
      }
   }
   return tree
}

//替换删除节点
func replaceNode(tree *binaryTree) *binaryTree{
   //删除的节点无左右节点
  if tree.leftNode == nil && tree.rightNode == nil {
      tree = &binaryTree{}
   }else if tree.leftNode == nil && tree.rightNode != nil {
      //左节点为空，右节点不为空
  tree = tree.rightNode
   }else if tree.rightNode == nil && tree.leftNode != nil {
      //右节点为空，左节点不为空
  tree = tree.leftNode
   }else{
      //节点左右节点都存在，则从右子树查找节点替代父节点
 //若右节点下没有左右节点,则直接用右节点的值替换，并删除右节点  
     if tree.rightNode.leftNode == nil && tree.rightNode.rightNode == nil {
         tree.value = tree.rightNode.value
         tree.rightNode = &binaryTree{}
      }else if tree.rightNode.leftNode == nil && tree.rightNode.rightNode != nil {
         //若右节点下左节点为空，右节点不为空，则右节点的值替换，并将右节点的右节点替换过来
  tree.value = tree.rightNode.value
         tree.rightNode = tree.rightNode.rightNode
      }else{
         //若右节点的左节点不为空
  tree.value = tree.rightNode.leftNode.value
         tree.rightNode.leftNode = replaceNode(tree.rightNode.leftNode)
      }
   }
   return tree
}

实现二叉查找树的完整代码如下,二叉查找树的中序遍历可获取到已排序完成的节点，所以这里用中序遍历来判断是否执行成功

package main

import "fmt"

type binaryTree struct {
    value int
    leftNode *binaryTree
    rightNode *binaryTree
}

func main(){

    var numArr = []int{10,11,4,2,8,1,3,6,9,5,7}

    tree := createBinarySearchTree(numArr)
    find := findNode(9,tree)
    fmt.Print(find)
    tree = deleteNode(4,tree)
    node := &binaryTree{13,nil,nil}
    tree = insertNode(tree,node)
    node = &binaryTree{1,nil,nil}

    var middle []int
    middle = middleForeach(*tree,middle)
    fmt.Println(middle)
}

//创建平衡二叉树
func createBinarySearchTree(nums []int) *binaryTree{
    tree := new(binaryTree)
    for index := range nums{
        node := &binaryTree{nums[index],nil,nil}
        tree = insertNode(tree,node)
    }
    return tree
}

//删除节点
func deleteNode(num int,tree *binaryTree) *binaryTree{
    //先查看删除的值是否存在树当中
    find := findNode(num,tree)
    if find {
        //配置到节点值，执行删除操作
        if tree.value == num {
            //删除的节点无左右节点
            if tree.leftNode == nil && tree.rightNode == nil {
                tree = &binaryTree{}
            }else if tree.leftNode == nil && tree.rightNode != nil {
                //左节点为空，右节点不为空
                tree = tree.rightNode
            }else if tree.rightNode == nil && tree.leftNode != nil {
                //右节点为空，左节点不为空
                tree = tree.leftNode
            }else{
                //节点左右节点都存在
                tree = replaceNode(tree)
            }
        }else if tree.value > num {
            tree.leftNode = deleteNode(num,tree.leftNode)
        }else {
            tree.rightNode = deleteNode(num,tree.rightNode)
        }
    }
    return tree
}

//替换删除节点
func replaceNode(tree *binaryTree) *binaryTree{
    //删除的节点无左右节点
    if tree.leftNode == nil && tree.rightNode == nil {
        tree = &binaryTree{}
    }else if tree.leftNode == nil && tree.rightNode != nil {
        //左节点为空，右节点不为空
        tree = tree.rightNode
    }else if tree.rightNode == nil && tree.leftNode != nil {
        //右节点为空，左节点不为空
        tree = tree.leftNode
    }else{
        //节点左右节点都存在，则从右子树查找节点替代父节点
        //若右节点下没有左右节点,则直接用右节点的值替换，并删除右节点
        if tree.rightNode.leftNode == nil && tree.rightNode.rightNode == nil {
            tree.value = tree.rightNode.value
            tree.rightNode = &binaryTree{}
        }else if tree.rightNode.leftNode == nil && tree.rightNode.rightNode != nil {
            //若右节点下左节点为空，右节点不为空，则右节点的值替换，并将右节点的右节点替换过来
            tree.value = tree.rightNode.value
            tree.rightNode = tree.rightNode.rightNode
        }else{
            //若右节点的左节点不为空
            tree.value = tree.rightNode.leftNode.value
            tree.rightNode.leftNode = replaceNode(tree.rightNode.leftNode)
        }
    }
    return tree
}

//节点查找
func findNode(num int,tree *binaryTree) bool{
    targetNode := tree
    for targetNode != nil{
        if targetNode.value == num {
            return true
        }else if targetNode.value > num {
            targetNode = targetNode.leftNode
        }else {
            targetNode = targetNode.rightNode
        }
    }
    return false
}

//节点插入
func insertNode(tree *binaryTree,node *binaryTree) *binaryTree {

    if tree.value == 0 {
        return node
    }
    if tree.value == node.value {
        return tree
    }else if tree.value > node.value {
        //往左子树走,为空则直接插入节点
        if tree.leftNode == nil {
            tree.leftNode = node
        }else {
            tree.leftNode = insertNode(tree.leftNode,node)
        }
    }else {
        //往右子树走,为空则直接插入节点
        if tree.rightNode == nil {
            tree.rightNode = node
        }else {
            tree.rightNode = insertNode(tree.rightNode,node)
        }
    }
    return tree
}

//中序遍历
func middleForeach(tree binaryTree,num []int) []int{
    var leftNum,rightNum []int
    //若存在左节点，遍历左节点树
    if tree.leftNode != nil {
        leftNum = middleForeach(*tree.leftNode,leftNum)
        for _,value := range leftNum{
            num = append(num,value)
        }
    }

    //先遍历根节点
    if tree.value != 0 {
        num = append(num,tree.value)
    }

    //若存在右节点，遍历右节点树
    if tree.rightNode != nil {
        rightNum = middleForeach(*tree.rightNode,rightNum)
        for _,value := range rightNum{
            num = append(num,value)
        }
    }

    return num
}

二叉树的缺陷

假设初始的二叉查找树只有三个节点，根节点为9，左孩子为8，右孩子为12

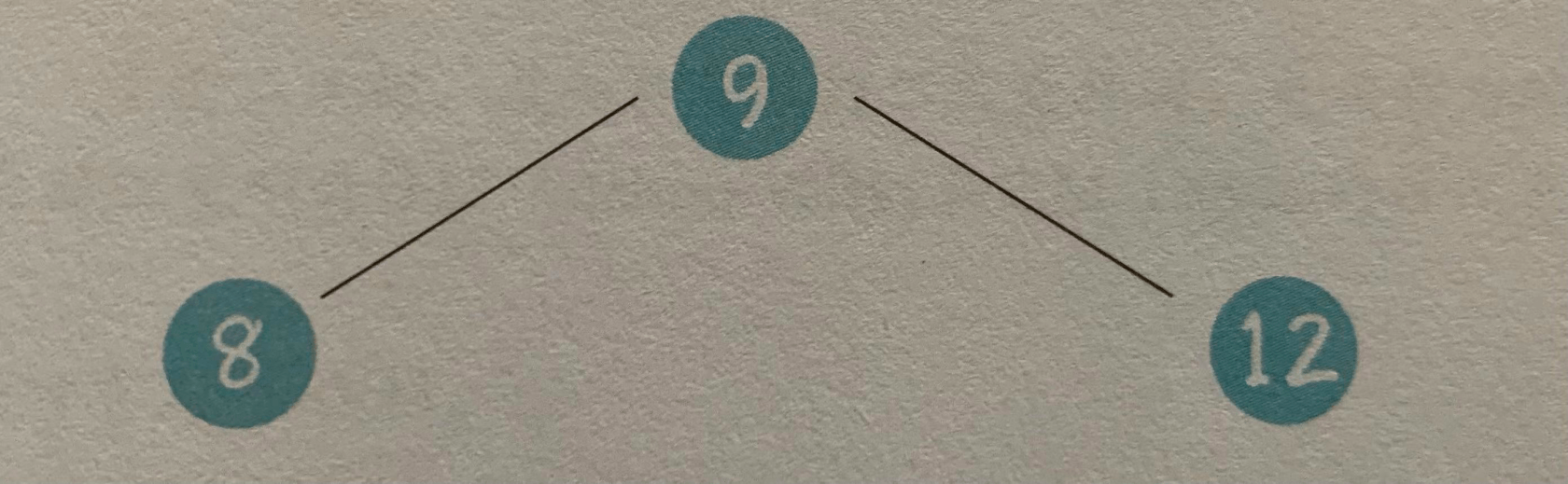
接下来我们依次插入如下五个节点：7，6，5，4，3。依照二叉查找树的特性，结果会变成什么样呢？

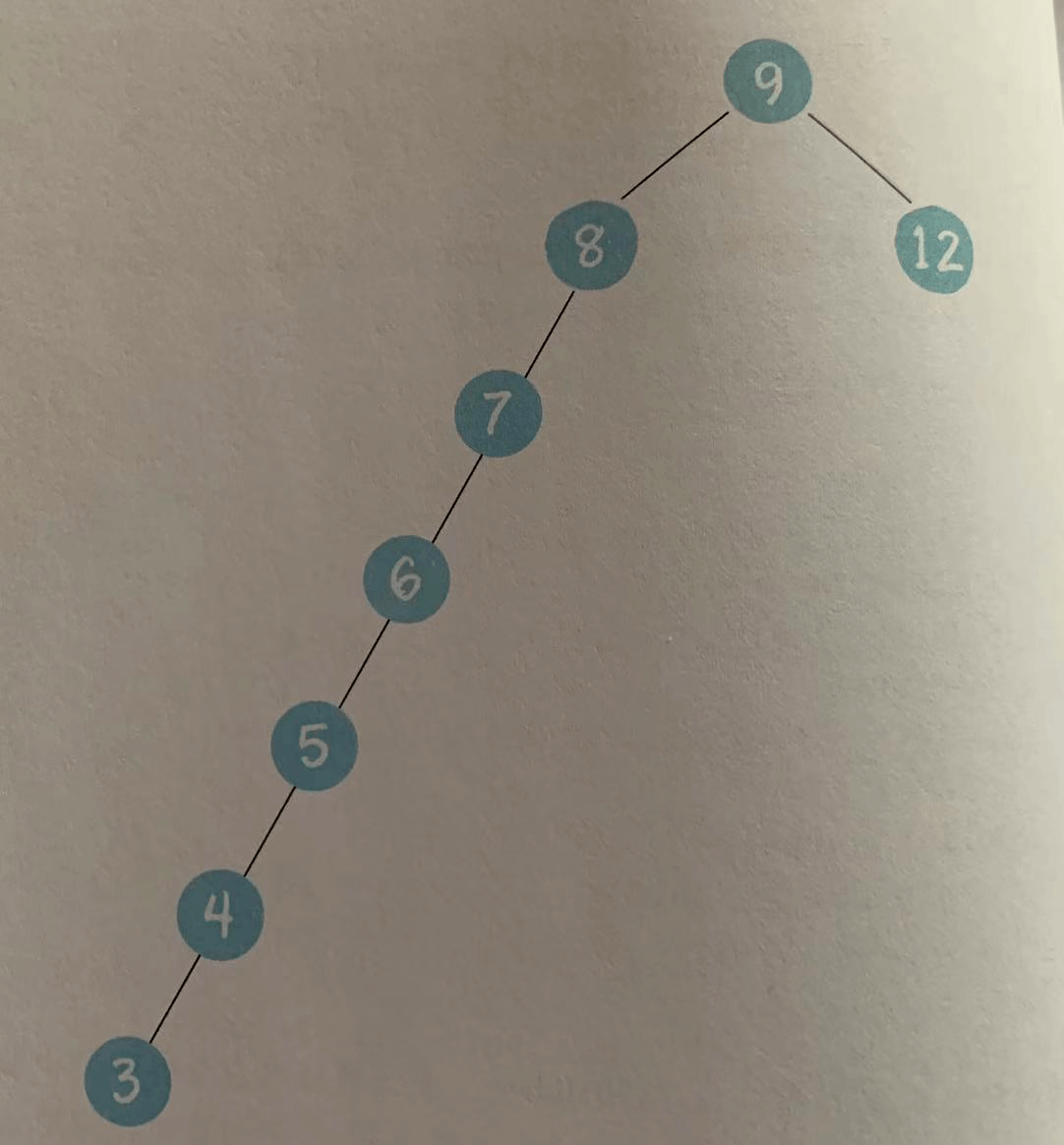
虽然这样一棵树也符合二叉查找树的特性，但是查找节点的时间复杂度退化成了O(n)

二叉平衡树

二叉平衡树是一种特性的二叉查找树，也被称为AVL树。它在每次插入、删除节点之后，可以进行“自平衡”，也就是通过一系列调整重新达到平衡状态。

平衡因子

下图就是一颗典型的AVL树，每个节点旁边都标注了平衡因子

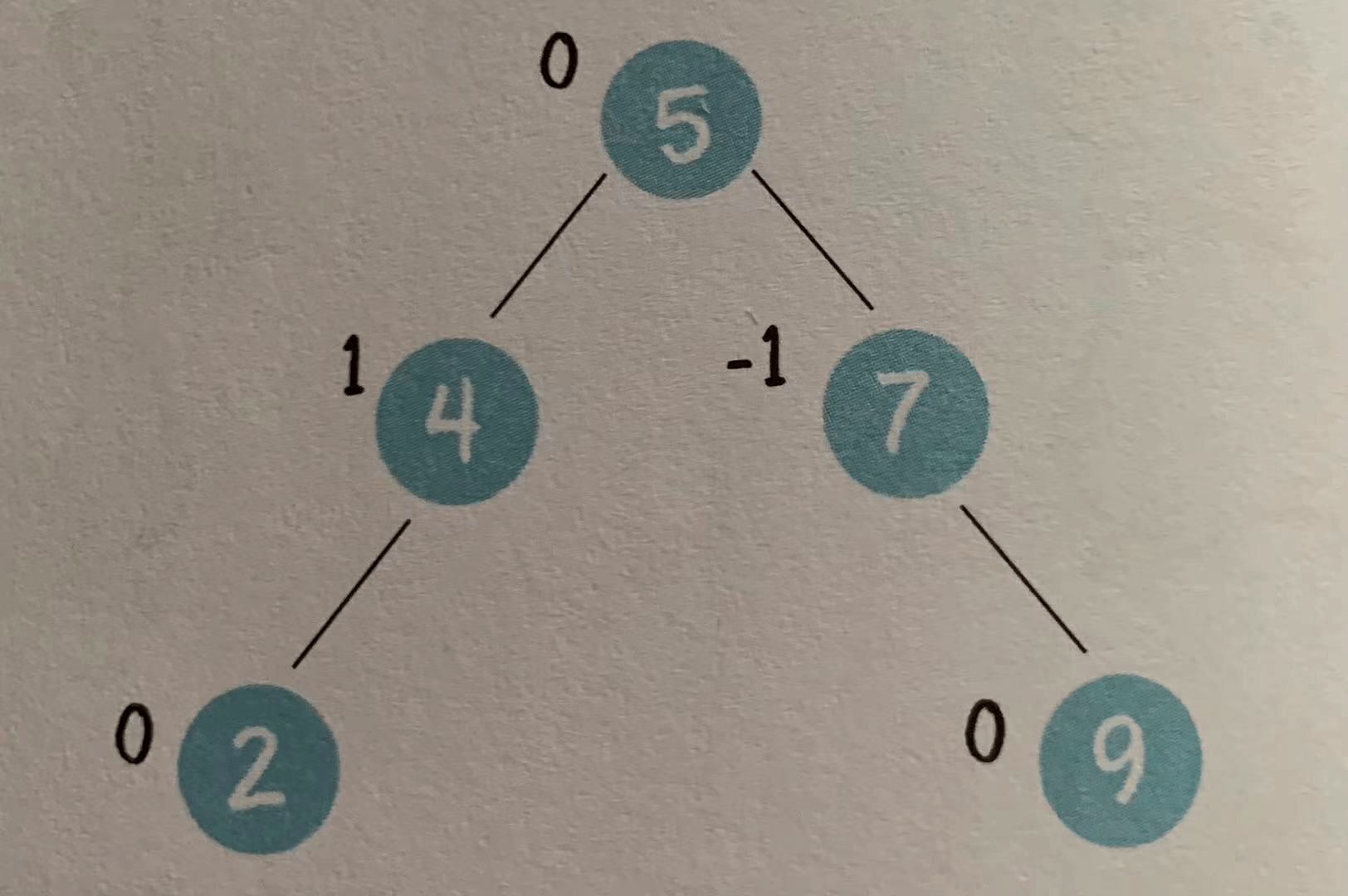
其中节点4的左子树高度是1，右子树不存在，所以该节点的平衡因子是1-0=1
其中7的左子树不存在，右子树高度是1，所以平衡因子是0-1=-1
所有的叶子节点，不存在左右子树，所以平衡因子都是0
AVL树对平衡因子的限制(只能是-1，0，1)，保证了任意节点的两棵树的高度差都不超过1，这种状态被称为高度平衡

以下是对计算树平衡因子的代码实现，首先要计算左右子树的高度，然后得到平衡因子，还添加了方法用于判断树是否达到平衡

//检查树是否达到平衡
func (tree binaryTree) isBalance() bool {
   if tree.RightNode == nil && tree.LeftNode == nil {
      return true
  }
   //节点的平衡因子
  factor := tree.getTreeFactor()
   if factor > 1 || factor < -1 {
      return false
  }
   return true
}

//获取节点的平衡因子
func (tree binaryTree) getTreeFactor() int{
    leftFactor,rightFactor := 0,0
    if tree.RightNode != nil {
        rightFactor = tree.RightNode.getTreeHeight()
    }
    if tree.LeftNode != nil {
        leftFactor = tree.LeftNode.getTreeHeight()
    }
    factor := float64(leftFactor - rightFactor)
    return int(factor)
}

//获取节点树高度，深度优先
func (tree binaryTree) getTreeHeight() int{
   //节点无
  if tree.RightNode == nil && tree.LeftNode == nil {
      return 1
  }
   leftHeight,rightHeight := 1,1
  if tree.LeftNode != nil && tree.LeftNode.Value != 0 {
      leftHeight = 1 + tree.LeftNode.getTreeHeight()
   }
   if tree.RightNode != nil && tree.RightNode.Value != 0{
      rightHeight = 1 + tree.RightNode.getTreeHeight()
   }
   //比较左右节点树高度
  height := math.Max(float64(leftHeight),float64(rightHeight))
   return int(height)
}

树平衡调整

当插入节点导致平衡因子被打破，这时候需要对树进行调整，AVL树调整可分为4种情况

1. 左左局面(LL)

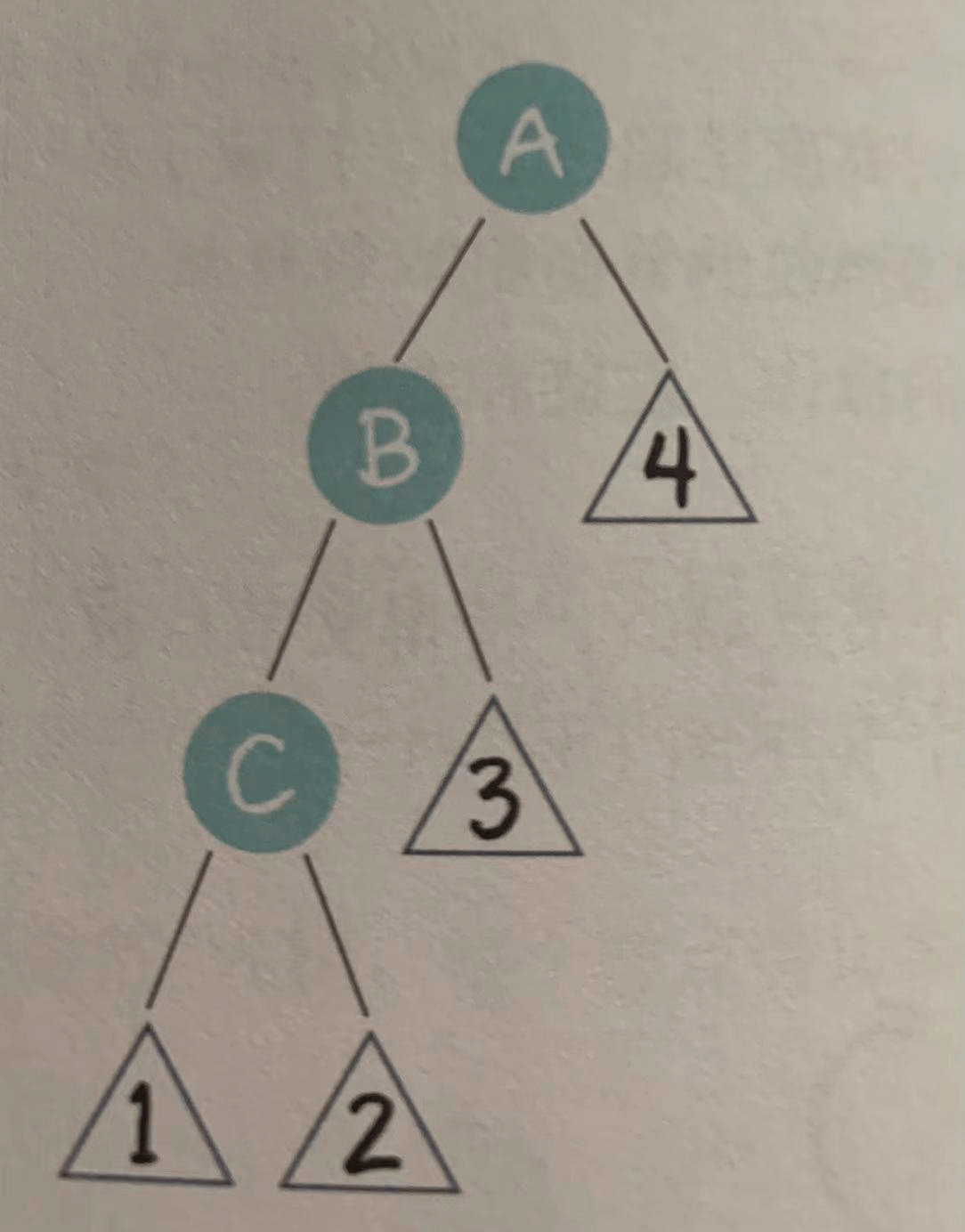
顾名思义，祖父节点A右一个左孩子节点B，而节点B又有一个左孩子节点C。标号1，2，3，4的三角形是各个节点的子树。

在这种局面下，我们以节点A为轴，进行右旋操作：

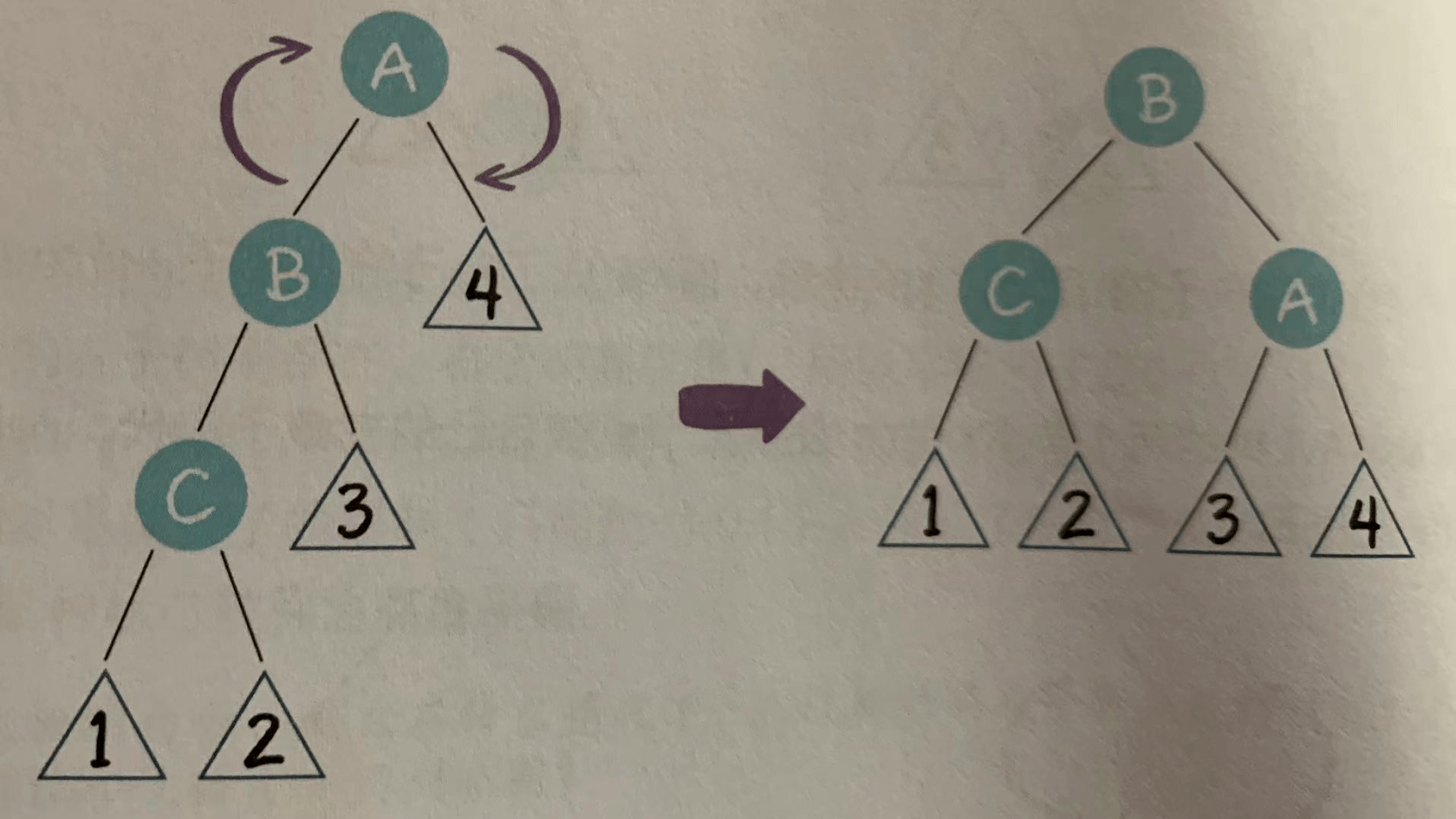
2. 右右局面(RR)

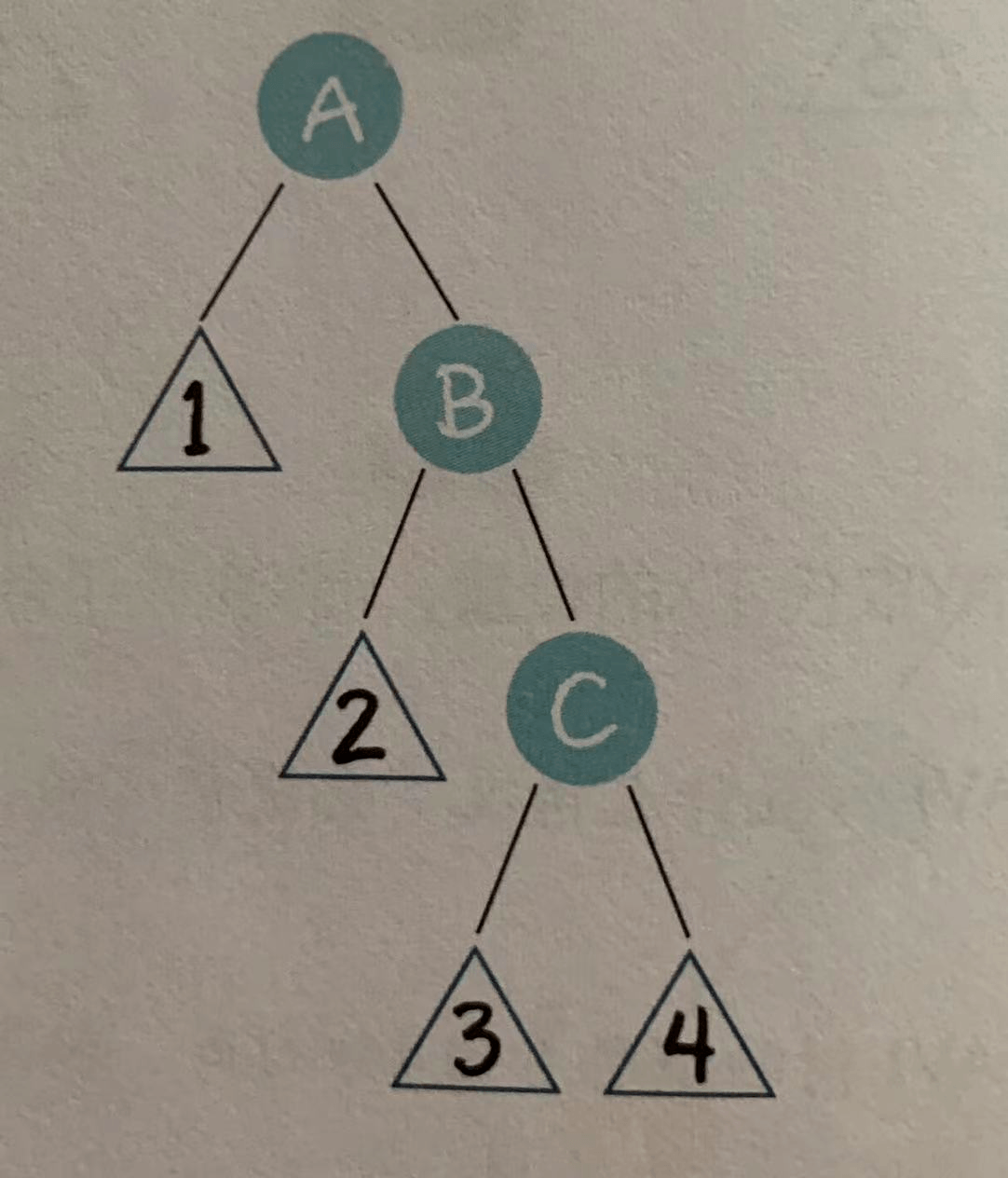
祖父节点A有一个右孩子节点B，而节点B又有一个右孩子节点C。
在这种局面下，我们以节点A为轴，进行左旋操作。

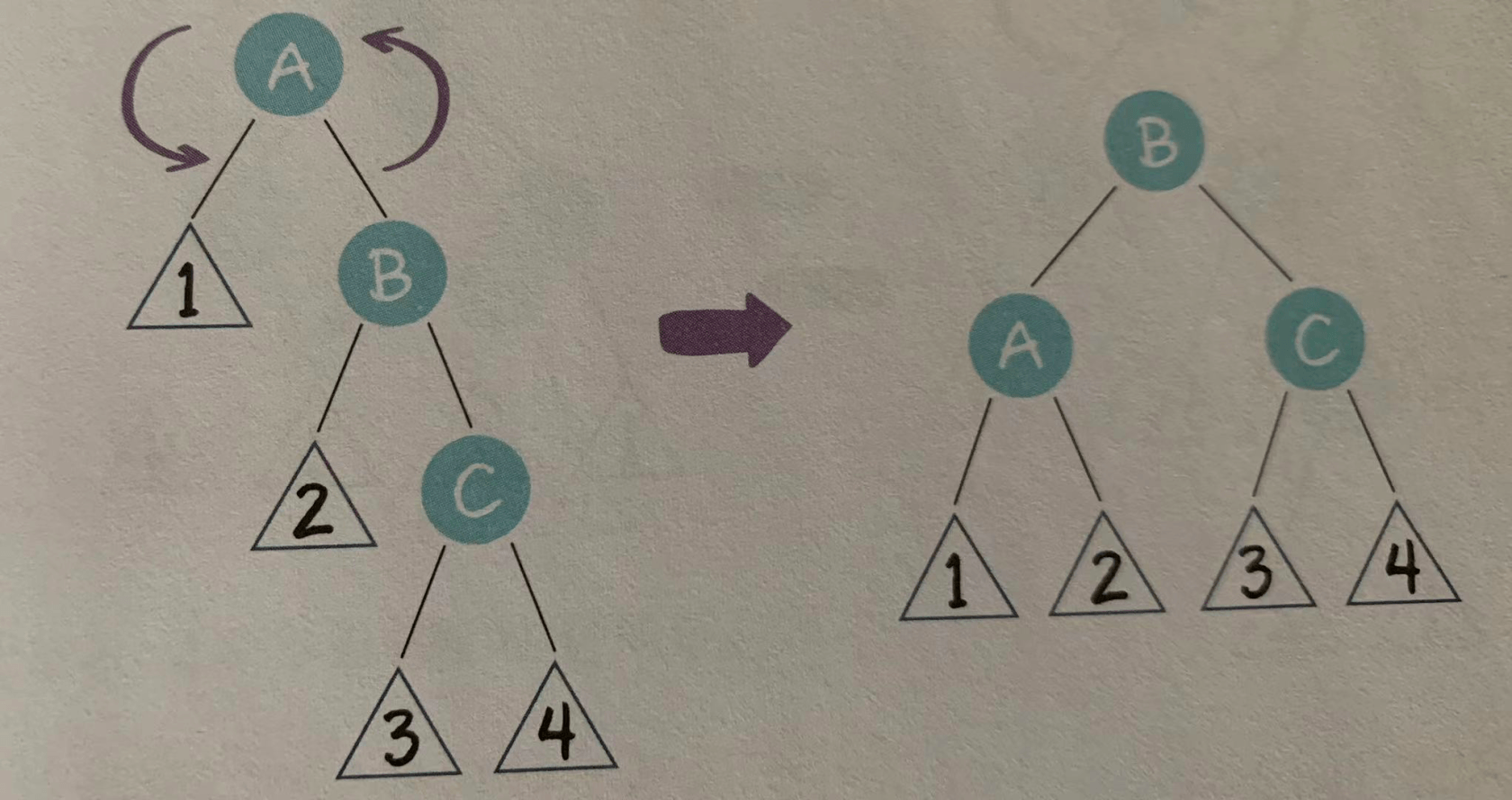
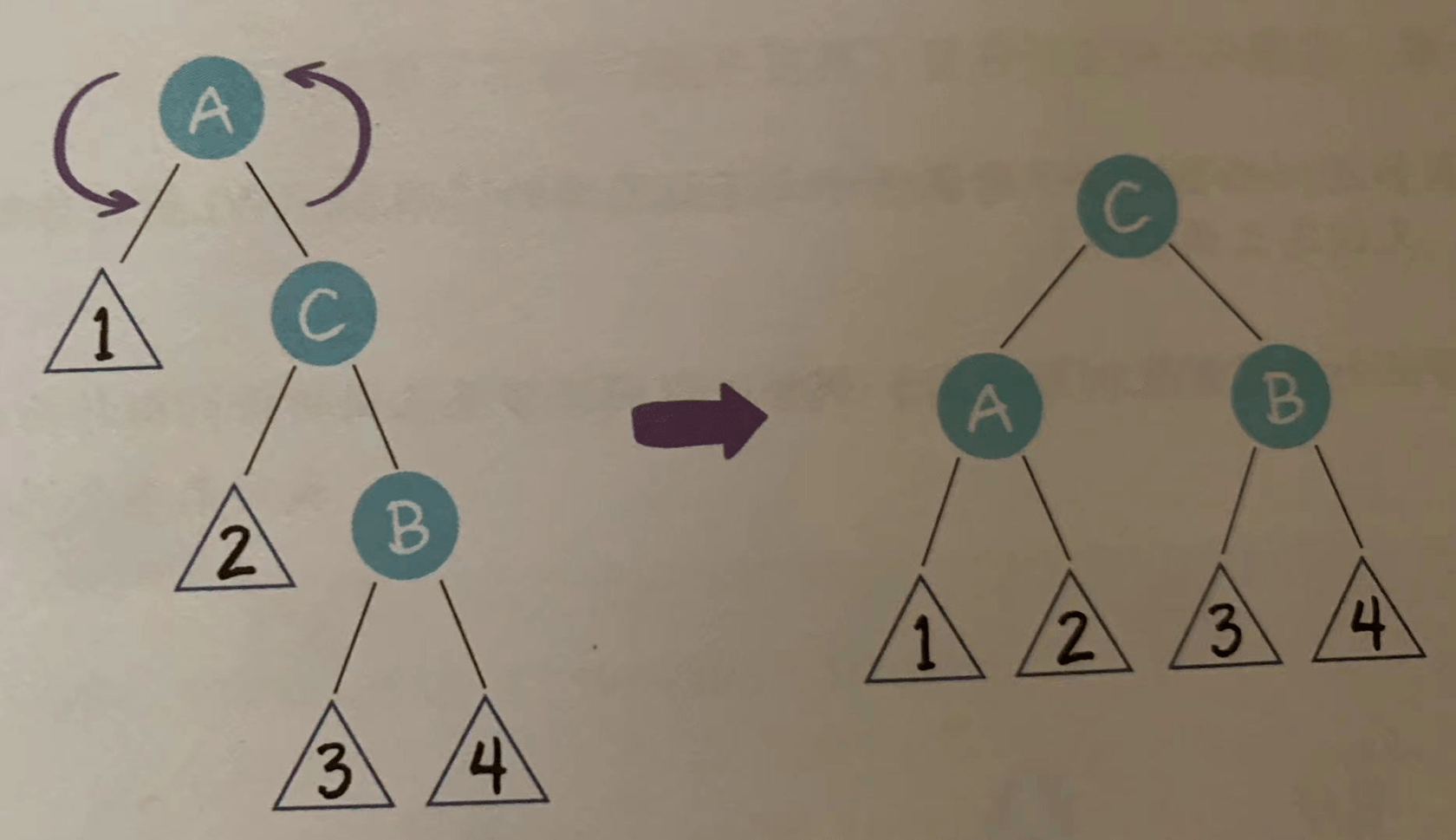
3. 左右局面(LR)

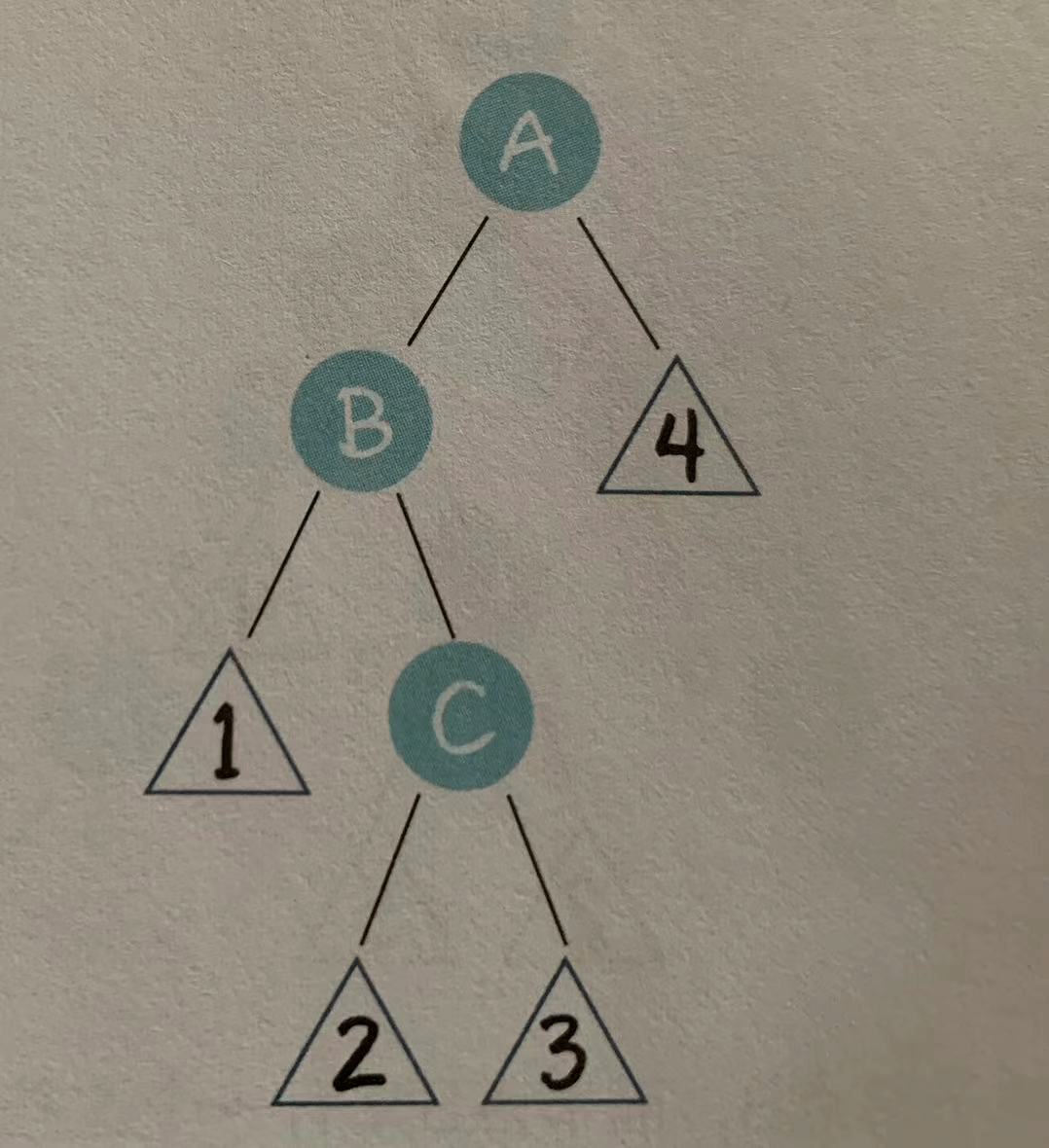
祖父节点A有一个左孩子节点B，而节点B又有一个右孩子节点C。
在这种局面下，我们先以节点B为轴，进行左旋操作。

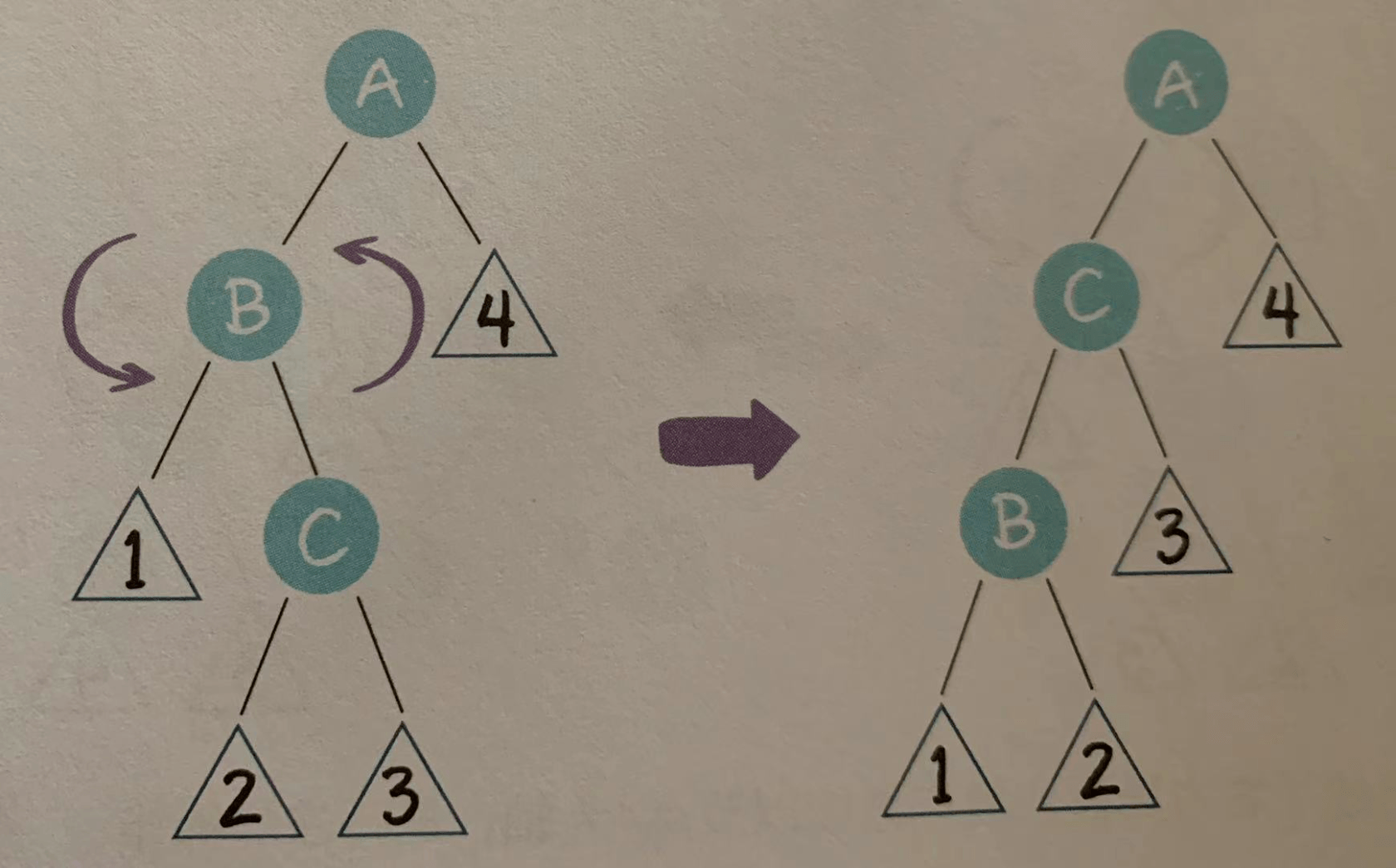
这样就转化成了左左局面。我们继续以节点A为轴，进行右旋操作。

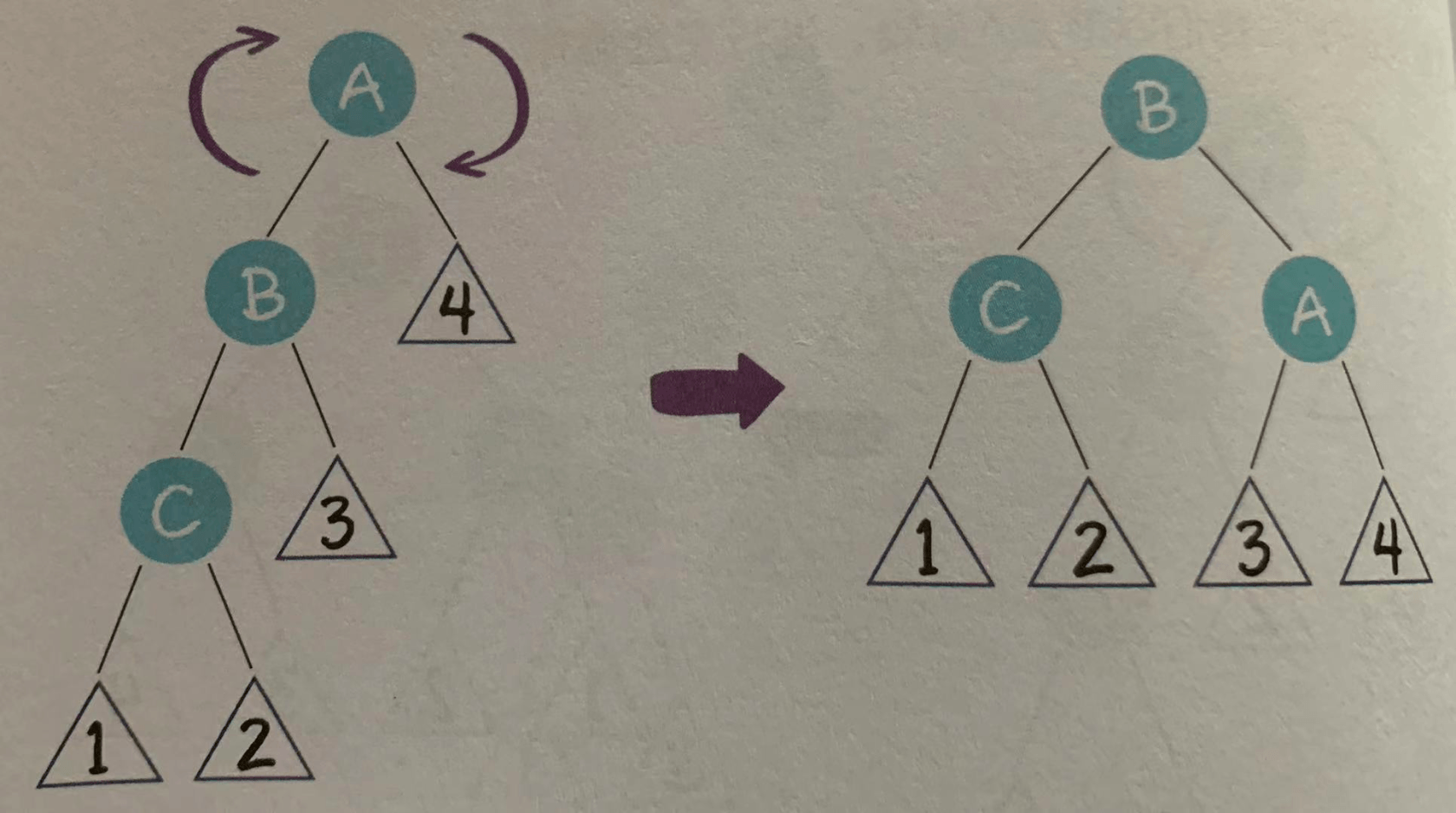
4. 右左局面(RL)

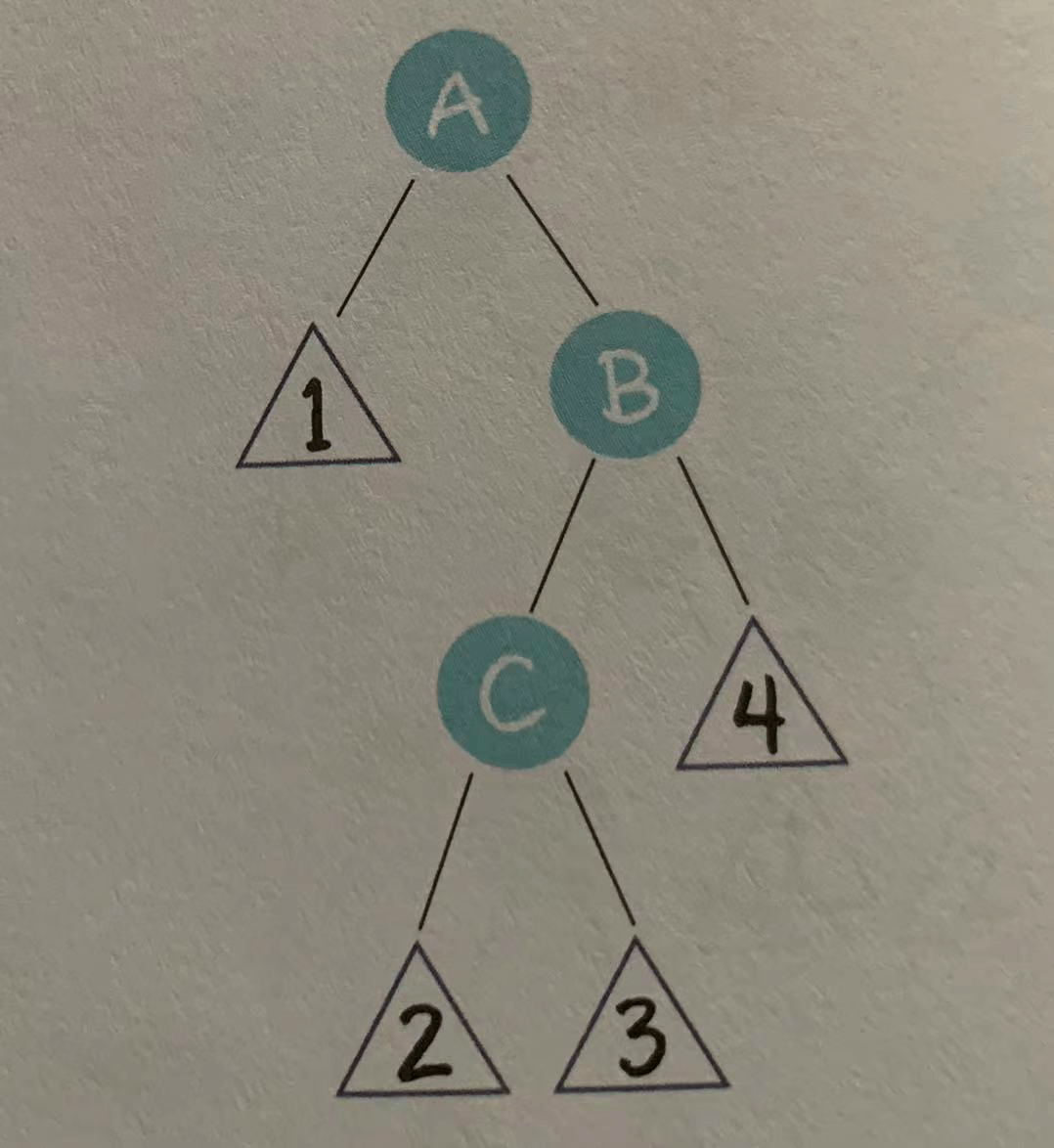
祖父节点A右一个右孩子节点B，而节点B又有一个左孩子节点C。
在这种局面下，我们先以节点B为轴，进行右旋操作。

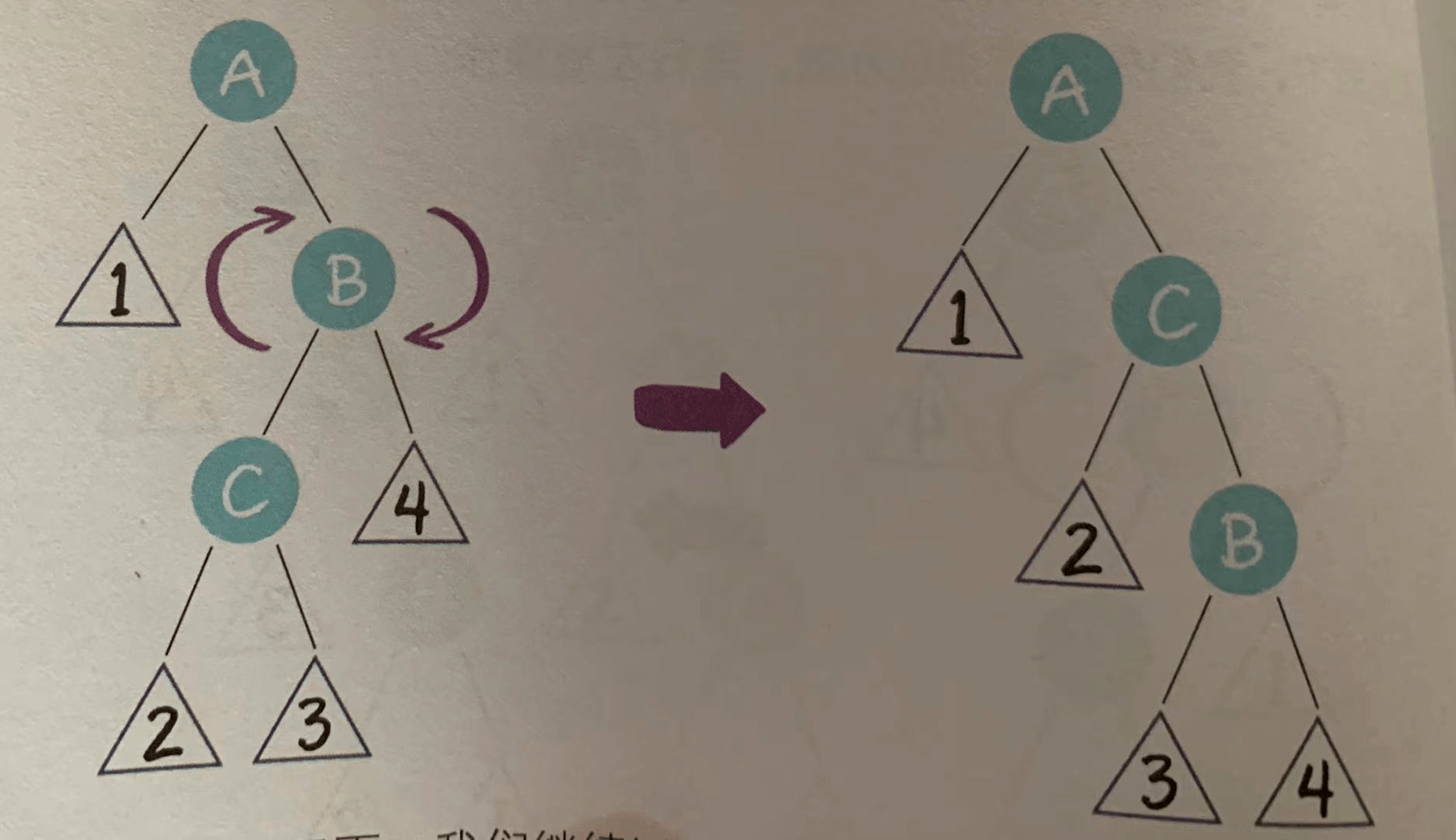
这样就转化成了右右局面。我们继续以节点A为轴，进行左旋操作。

代码实现如下：

//左左局面
func LeftLeftRotate(tree *binaryTree) *binaryTree{
    //原节点左节点成为根节点
    mainNode := tree.LeftNode
    changeNode := &binaryTree{}
    //判断原节点左节点是否存在
    if mainNode.RightNode != nil {
        changeNode = mainNode.RightNode
    }
    mainRightNode := tree
    mainRightNode.LeftNode = changeNode
    //刷新树高度
    mainRightNode.Height = mainRightNode.getTreeHeight()
    mainNode.RightNode = mainRightNode
    mainNode.Height = mainNode.getTreeHeight()
    return mainNode
}

//右右局面
func RightRightRotate(tree *binaryTree) *binaryTree{
    mainNode := tree.RightNode
    changeNode := &binaryTree{}
    if mainNode.LeftNode != nil {
        changeNode = mainNode.LeftNode
    }
    mainLeftNode := tree
    mainLeftNode.RightNode = changeNode
    mainLeftNode.Height = mainLeftNode.getTreeHeight()
    mainNode.LeftNode = mainLeftNode
    mainNode.Height = mainNode.getTreeHeight()
    return mainNode
}

//左右局面
func LeftRightRotate(tree *binaryTree) *binaryTree{
    mainLeftNode := tree.LeftNode
    changeNode := &binaryTree{}
    mainNode := mainLeftNode.RightNode
    if mainNode.LeftNode != nil {
        changeNode = mainNode.LeftNode
    }
    mainLeftNode.RightNode = changeNode
    mainLeftNode.Height = mainLeftNode.getTreeHeight()
    mainNode.LeftNode = mainLeftNode
    mainNode.Height = mainNode.getTreeHeight()
    tree.LeftNode = mainNode
    tree = LeftLeftRotate(tree)
    return tree
}

//右左局面
func RightLightRotate(tree *binaryTree) *binaryTree{
    mainRightNode := tree.RightNode
    changeNode := &binaryTree{}
    mainNode := mainRightNode.LeftNode
    if mainNode.RightNode != nil {
        changeNode = mainNode.RightNode
    }
    mainRightNode.LeftNode = changeNode
    mainRightNode.Height = mainRightNode.getTreeHeight()
    mainNode.RightNode = mainRightNode
    mainNode.Height = mainNode.getTreeHeight()
    tree.RightNode = mainNode
    tree = RightRightRotate(tree)
    return tree
}

二叉平衡树的插入和删除

在代码实现上，可以复用二叉查找树的代码逻辑，在二叉查找树的基础上添加逻辑，在节点的插入和删除后，添加判断逻辑，判断二叉平衡树的平衡是否被破坏，若被破坏则进行相关的调整，过程就不多赘述，直接上完整实现代码

package main

import (
    "fmt"
    "math"
)

type binaryTree struct {
    Value int
    Height int
    LeftNode *binaryTree
    RightNode *binaryTree
}

func main(){
    var numArr = []int{10,11,4,2,8,1,3,6,9,5,7,12}
    tree := createBinaryBalanceTree(numArr)
    var middle []int
    tree = deleteNode(9,tree)
    tree = deleteNode(11,tree)
    tree = deleteNode(12,tree)
    fmt.Println("\n")
    middle := middleForeach(*tree,middle)
    fmt.Println(middle,"\n")
}


//获取节点树高度，深度优先
func (tree binaryTree) getTreeHeight() int{
    //节点无
    if tree.RightNode == nil && tree.LeftNode == nil {
        return 1
    }
    leftHeight,rightHeight := 1,1
    if tree.LeftNode != nil && tree.LeftNode.Value != 0 {
        leftHeight = 1 + tree.LeftNode.getTreeHeight()
    }
    if tree.RightNode != nil && tree.RightNode.Value != 0{
        rightHeight = 1 + tree.RightNode.getTreeHeight()
    }
    //比较左右节点树高度
    height := math.Max(float64(leftHeight),float64(rightHeight))
    return int(height)
}

//检查树是否达到平衡
func (tree binaryTree) isBalance() bool {
    if tree.RightNode == nil && tree.LeftNode == nil {
        return true
    }
    //节点的平衡因子
    factor := tree.getTreeFactor()
    if factor > 1 || factor < -1 {
        return false
    }
    return true
}

//获取节点的平衡因子
func (tree binaryTree) getTreeFactor() int{
    leftFactor,rightFactor := 0,0
    if tree.RightNode != nil {
        rightFactor = tree.RightNode.getTreeHeight()
    }
    if tree.LeftNode != nil {
        leftFactor = tree.LeftNode.getTreeHeight()
    }
    factor := float64(leftFactor - rightFactor)
    return int(factor)
}

//创建二叉平衡树
func createBinaryBalanceTree(nums []int) *binaryTree{
    tree := new(binaryTree)
    for index := range nums{
        node := &binaryTree{Value: nums[index]}
        tree = insertNode(tree,node)
    }
    return tree
}

//插入节点
func insertNode(tree *binaryTree,node *binaryTree) *binaryTree {

    if tree.Value == 0 {
        return node
    }
    if tree.Value == node.Value {
        return tree
    }else if tree.Value > node.Value {
        //往左子树走,为空则直接插入节点
        if tree.LeftNode == nil {
            tree.LeftNode = node
        }else {
            tree.LeftNode = insertNode(tree.LeftNode,node)
        }
        //节点高度重置
        tree.LeftNode.Height = tree.LeftNode.getTreeHeight()
    }else {
        //往右子树走,为空则直接插入节点
        if tree.RightNode == nil {
            tree.RightNode = node
        }else {
            tree.RightNode = insertNode(tree.RightNode,node)
        }
        //节点高度重置
        tree.RightNode.Height = tree.RightNode.getTreeHeight()
    }
    //节点高度重置
    tree.Height = tree.getTreeHeight()
    //节点不平衡
    if !tree.isBalance() {
        //tree = treeInsertRotateBalance(node,tree)
        //左子树偏大
        if tree.getTreeFactor() > 1 {
            if node.Value < tree.LeftNode.Value {
                tree = LeftLeftRotate(tree)
            }else {
                tree = LeftRightRotate(tree)
            }
        }else {
            //右子树偏大
            if node.Value > tree.RightNode.Value {
                tree = RightRightRotate(tree)
            }else {
                tree = RightLightRotate(tree)
            }
        }
    }
    return tree
}


//删除节点
func deleteNode(num int,tree *binaryTree) *binaryTree{
    //先查看删除的值是否存在树当中
    find := findNode(num,tree)
    if find {
        //配置到节点值，执行删除操作
        if tree.Value == num {
            //删除的节点无左右节点
            if tree.LeftNode == nil && tree.RightNode == nil {
                tree = &binaryTree{}
            }else if tree.LeftNode == nil && tree.RightNode != nil {
                //左节点为空，右节点不为空
                tree = tree.RightNode
            }else if tree.RightNode == nil && tree.LeftNode != nil {
                //右节点为空，左节点不为空
                tree = tree.LeftNode
            }else{
                //节点左右节点都存在
                tree = replaceNode(tree)
            }
        }else if tree.Value > num {
            tree.LeftNode = deleteNode(num,tree.LeftNode)
        }else {
            tree.RightNode = deleteNode(num,tree.RightNode)
        }
        tree.Height = tree.getTreeHeight()
    }
    if !tree.isBalance() {
        if tree.getTreeFactor() > 1 {
            if num > tree.Value {
                tree = LeftLeftRotate(tree)
            }else {
                tree = LeftRightRotate(tree)
            }
        }else {
            if num < tree.Value {
                tree = RightRightRotate(tree)
            }else {
                tree = RightLightRotate(tree)
            }
        }
    }
    return tree
}

//替换删除节点
func replaceNode(tree *binaryTree) *binaryTree{
    //删除的节点无左右节点
    if tree.LeftNode == nil && tree.RightNode == nil {
        tree = &binaryTree{}
    }else if tree.LeftNode == nil && tree.RightNode != nil {
        //左节点为空，右节点不为空
        tree = tree.RightNode
    }else if tree.RightNode == nil && tree.LeftNode != nil {
        //右节点为空，左节点不为空
        tree = tree.LeftNode
    }else{
        //节点左右节点都存在，则从右子树查找节点替代父节点
        //若右节点下没有左右节点,则直接用右节点的值替换，并删除右节点
        if tree.RightNode.LeftNode == nil && tree.RightNode.RightNode == nil {
            tree.Value = tree.RightNode.Value
            tree.RightNode = &binaryTree{}
        }else if tree.RightNode.LeftNode == nil && tree.RightNode.RightNode != nil {
            //若右节点下左节点为空，右节点不为空，则右节点的值替换，并将右节点的右节点替换过来
            tree.Value = tree.RightNode.Value
            tree.RightNode = tree.RightNode.RightNode
        }else{
            //若右节点的左节点不为空
            tree.Value = tree.RightNode.LeftNode.Value
            tree.RightNode.LeftNode = replaceNode(tree.RightNode.LeftNode)
        }
    }
    return tree
}

//左左局面
func LeftLeftRotate(tree *binaryTree) *binaryTree{
    //原节点左节点成为根节点
    mainNode := tree.LeftNode
    changeNode := &binaryTree{}
    //判断原节点左节点是否存在
    if mainNode.RightNode != nil {
        changeNode = mainNode.RightNode
    }
    mainRightNode := tree
    mainRightNode.LeftNode = changeNode
    //刷新树高度
    mainRightNode.Height = mainRightNode.getTreeHeight()
    mainNode.RightNode = mainRightNode
    mainNode.Height = mainNode.getTreeHeight()
    return mainNode
}

//右右局面
func RightRightRotate(tree *binaryTree) *binaryTree{
    mainNode := tree.RightNode
    changeNode := &binaryTree{}
    if mainNode.LeftNode != nil {
        changeNode = mainNode.LeftNode
    }
    mainLeftNode := tree
    mainLeftNode.RightNode = changeNode
    mainLeftNode.Height = mainLeftNode.getTreeHeight()
    mainNode.LeftNode = mainLeftNode
    mainNode.Height = mainNode.getTreeHeight()
    return mainNode
}

//左右局面
func LeftRightRotate(tree *binaryTree) *binaryTree{
    mainLeftNode := tree.LeftNode
    changeNode := &binaryTree{}
    mainNode := mainLeftNode.RightNode
    if mainNode.LeftNode != nil {
        changeNode = mainNode.LeftNode
    }
    mainLeftNode.RightNode = changeNode
    mainLeftNode.Height = mainLeftNode.getTreeHeight()
    mainNode.LeftNode = mainLeftNode
    mainNode.Height = mainNode.getTreeHeight()
    tree.LeftNode = mainNode
    tree = LeftLeftRotate(tree)
    return tree
}

//右左局面
func RightLightRotate(tree *binaryTree) *binaryTree{
    mainRightNode := tree.RightNode
    changeNode := &binaryTree{}
    mainNode := mainRightNode.LeftNode
    if mainNode.RightNode != nil {
        changeNode = mainNode.RightNode
    }
    mainRightNode.LeftNode = changeNode
    mainRightNode.Height = mainRightNode.getTreeHeight()
    mainNode.RightNode = mainRightNode
    mainNode.Height = mainNode.getTreeHeight()
    tree.RightNode = mainNode
    tree = RightRightRotate(tree)
    return tree
}

//节点查找
func findNode(num int,tree *binaryTree) bool{
    targetNode := tree
    for targetNode != nil{
        if targetNode.Value == num {
            return true
        }else if targetNode.Value > num {
            targetNode = targetNode.LeftNode
        }else {
            targetNode = targetNode.RightNode
        }
    }
    return false
}

//中序遍历
func middleForeach(tree binaryTree,num []int) []int{
    var leftNum,rightNum []int
    //若存在左节点，遍历左节点树
    if tree.LeftNode != nil {
        leftNum = middleForeach(*tree.LeftNode,leftNum)
        for _,value := range leftNum{
            num = append(num,value)
        }
    }

    //先遍历根节点
    if tree.Value != 0 {
        num = append(num,tree.Value)
    }

    //若存在右节点，遍历右节点树
    if tree.RightNode != nil {
        rightNum = middleForeach(*tree.RightNode,rightNum)
        for _,value := range rightNum{
            num = append(num,value)
        }
    }

    return num
}

代码实现上相对有点复杂，在开始编写的时候还是有点难度，但是完成后发现给自己带来了特别大的成就感，或许这也是写代码的乐趣吧。后续会继续学习，争取把红黑树也实现了。

本作品采用《CC 协议》，转载必须注明作者和本文链接