数据结构与算法整理总结---优先搜索，字符串匹配

什么是“搜索”算法？

算法是作⽤于具体数据结构之上的，深度优先搜索算法和⼴度优先搜索算法都是基于“图”这种数据结构的。这是因为，图这种数据结构的表达能⼒很强，⼤部分涉及搜索的场景都可以抽象成“图”。

图上的搜索算法，最直接的理解就是，在图中找出从⼀个顶点出发，到另⼀个顶点的路径。具体⽅法有很多，⽐如今天要讲的两种最简单、最“暴⼒”的深度优先、⼴度优先搜索，还有A、IDA等启发式搜索算法。

⼴度优先搜索（BFS）

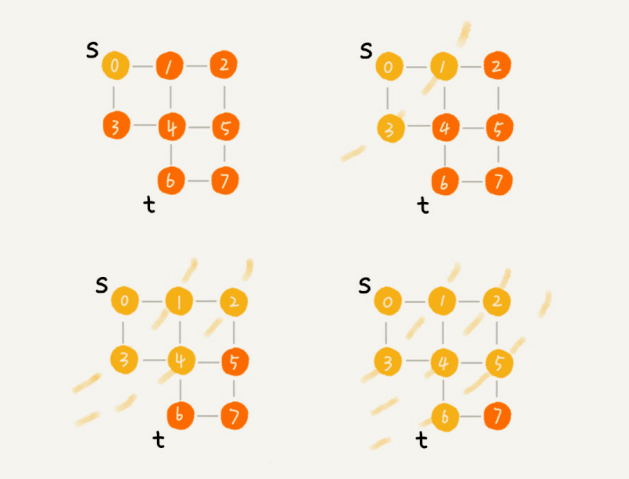
⼴度优先搜索（Breadth-First-Search），我们平常都把简称为BFS。直观地讲，它其实就是⼀种“地毯式”层层推进的搜索策略，即先查找离起始顶点最近的，然后是次近的，依次往外搜索。

深度优先搜索（DFS）

深度优先搜索（Depth-First-Search），简称DFS。最直观的例⼦就是“⾛迷宫”。

假设你站在迷宫的某个岔路⼝，然后想找到出⼝。你随意选择⼀个岔路⼝来⾛，⾛着⾛着发现⾛不通的时候，你就回退到上⼀个岔路⼝，重新选择⼀条路继续⾛，直到最终找到出⼝。这种⾛法就是⼀种深度优先搜索策略。

⾛迷宫的例⼦很容易能看懂，我们现在再来看下，如何在图中应⽤深度优先搜索，来找某个顶点到另⼀个顶点的路径。

你可以看我画的这幅图。搜索的起始顶点是s，终⽌顶点是t，我们希望在图中寻找⼀条从顶点s到顶点t的路径。如果映射到迷宫那个例⼦，s就是你起始所在的位置，t就是出⼝。

深度递归算法，把整个搜索的路径标记出来了。这⾥⾯实线箭头表示遍历，虚线箭头表示回退。从图中我们可以看出，深度优先搜索找出来的路径，并不是顶点s到顶点t的最短路径。

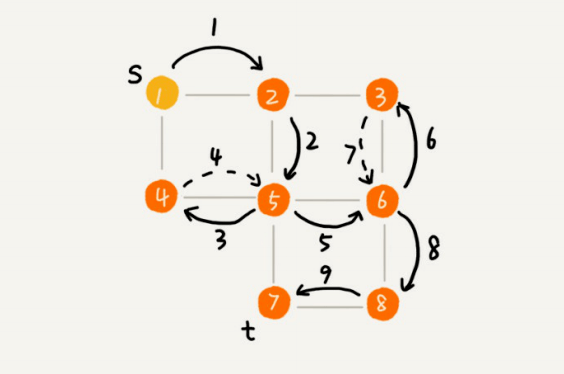
实际上，深度优先搜索⽤的是⼀种⽐较著名的算法思想，回溯思想。这种思想解决问题的过程，⾮常适合⽤递归来实现。

字符串匹配

BF算法

BF算法中的BF是Brute Force的缩写，中⽂叫作暴⼒匹配算法，也叫朴素匹配算法。从名字可以看出，这种算法的字符串匹配⽅式很“暴⼒”，当然也就会⽐较简单、好懂，但相应的性能也不⾼。

在开始讲解这个算法之前，先定义两个概念。它们分别是主串和模式串。这俩概念很好理解。

⽐⽅说，我们在字符串A中查找字符串B，那字符串A就是主串，字符串B就是模式串。我们把主串的⻓度记作n，模式串的⻓度记作m。因为我们是在主串中查找模式串，所以n>m。

作为最简单、最暴⼒的字符串匹配算法，BF算法的思想可以⽤⼀句话来概括，那就是，我们在主串中，检查起始位置分别是0、1、2…n-m且⻓度为m的n-m+1个⼦串，看有没有跟模式串匹配的。

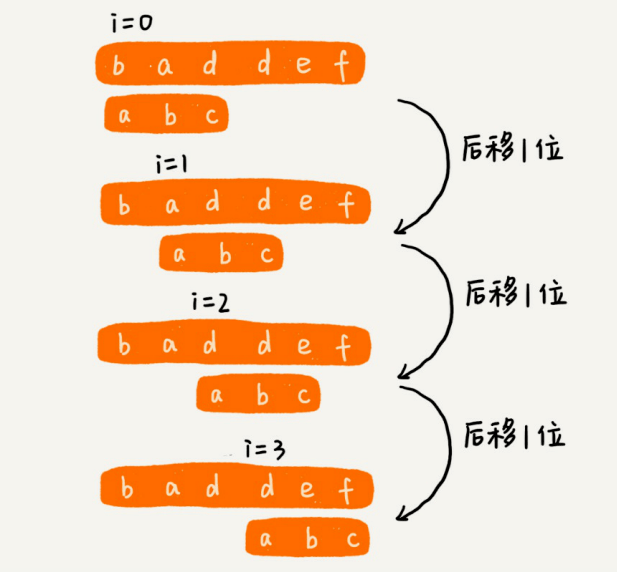
从上⾯的算法思想和例⼦，我们可以看出，在极端情况下，⽐如主串是“aaaaa…aaaaaa”（省略号表示有很多重复的字符a），模式串是“aaaaab”。我们每次都⽐对m个字符，要⽐对n-m+1次，所以，这种算法的最坏情况时间复杂度是O(n*m)。

尽管理论上，BF算法的时间复杂度很⾼，是O(n*m)，但在实际的开发中，它却是⼀个⽐较常⽤的字符串匹配算法。为什么这么说呢？原因有两点。

第⼀，实际的软件开发中，⼤部分情况下，模式串和主串的⻓度都不会太⻓。⽽且每次模式串与主串中的⼦串匹配的时候，当中途遇到不能匹配的字符的时候，就可以就停⽌了，不需要把m个字符都⽐对⼀下。所以，尽管理论上的最坏情况时间复杂度是O(n*m)，但是，统计意义上，⼤部分情况下，算法执⾏效率要⽐这个⾼很多。

第⼆，朴素字符串匹配算法思想简单，代码实现也⾮常简单。简单意味着不容易出错，如果有bug也容易暴露和修复。在⼯程中，在满⾜性能要求的前提下，简单是⾸选。

RK算法

RK算法的全称叫Rabin-Karp算法，是由它的两位发明者Rabin和Karp的名字来命名的。这个算法理解起来也不是很难。它其实就是刚刚讲的BF算法的升级版。

讲BF算法的时候讲过，如果模式串⻓度为m，主串⻓度为n，那在主串中，就会有n-m+1个⻓度为m的⼦串，我们只需要暴⼒地对⽐这n-m+1个⼦串与模式串，就可以找出主串与模式串匹配的⼦串。但是，每次检查主串与⼦串是否匹配，需要依次⽐对每个字符，所以BF算法的时间复杂度就⽐较⾼，是O(n*m)。我们对朴素的字符串匹配算法稍加改造，引⼊哈希算法，时间复杂度⽴刻就会降低。

RK算法的思路是这样的：我们通过哈希算法对主串中的n-m+1个⼦串分别求哈希值，然后逐个与模式串的哈希值⽐较⼤⼩。如果某个⼦串的哈希值与模式串相等，那就说明对应的⼦串和模式串匹配了（这⾥先不考虑哈希冲突的问题，后⾯我们会讲到）。因为哈希值是⼀个数字，数字之间⽐较是否相等是⾮常快速的，所以模式串和⼦串⽐较的效率就提⾼了。

不过，通过哈希算法计算⼦串的哈希值的时候，我们需要遍历⼦串中的每个字符。尽管模式串与⼦串⽐较的效率提⾼了，但是，算法整体的效率并没有提⾼。

BM算法

我们把模式串和主串的匹配过程，看作模式串在主串中不停地往后滑动。当遇到不匹配的字符时，BF算法和RK算法的做法是，模式串往后滑动⼀位，然后从模式串的第⼀个字符开始重新匹配。

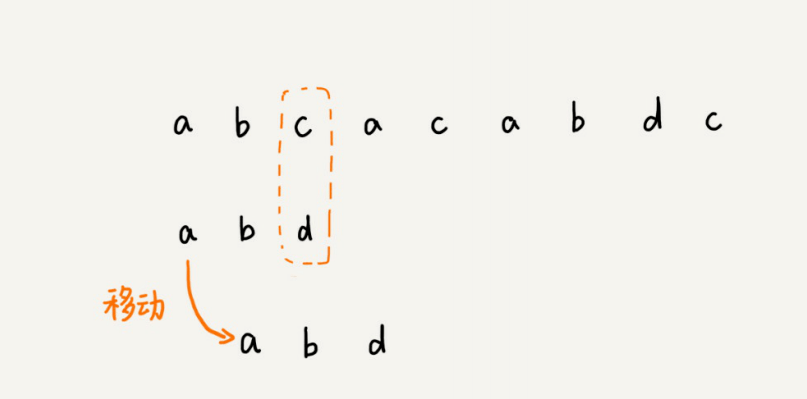
主串中的c，在模式串中是不存在的，所以，模式串向后滑动的时候，只要c与模式串有重合，肯定⽆法匹配。所以，我们可以⼀次性把模式串往后多滑动⼏位，把模式串移动到c的后⾯。

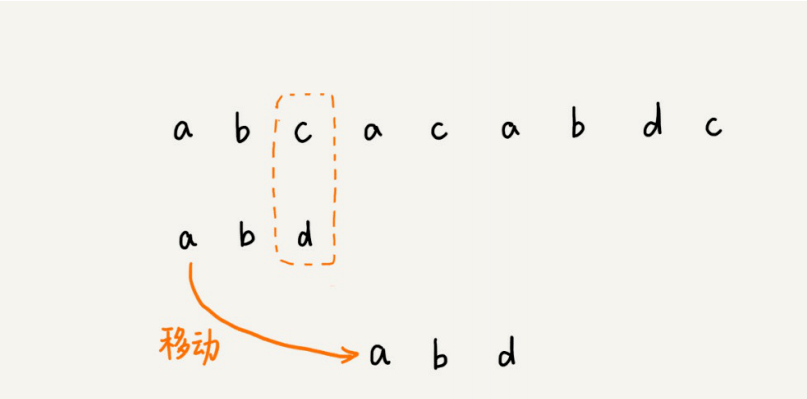
由现象找规律，当遇到不匹配的字符时，有什么固定的规律，可以将模式串往后多滑动⼏位呢？这样⼀次性往后滑动好⼏位，那匹配的效率岂不是就提⾼了？

BM算法，本质上其实就是在寻找这种规律。借助这种规律，在模式串与主串匹配的过程中，当模式串和主串某个字符不匹配的时候，能够跳过⼀些肯定不会匹配的情况，将模式串往后多滑动⼏位。

BM算法原理分析

BM算法包含两部分，分别是坏字符规则（bad character rule）和好后缀规则（good suffifix shift）。

1.坏字符规则

在匹配的过程中，我们都是按模式串的下标从⼩到⼤的顺序，依次与主串中的字符进⾏匹配的。这种匹配顺序⽐较符合我们的思维习惯，⽽BM算法的匹配顺序⽐较特别，它是按照模式串下标从⼤到⼩的顺序，倒着匹配的。

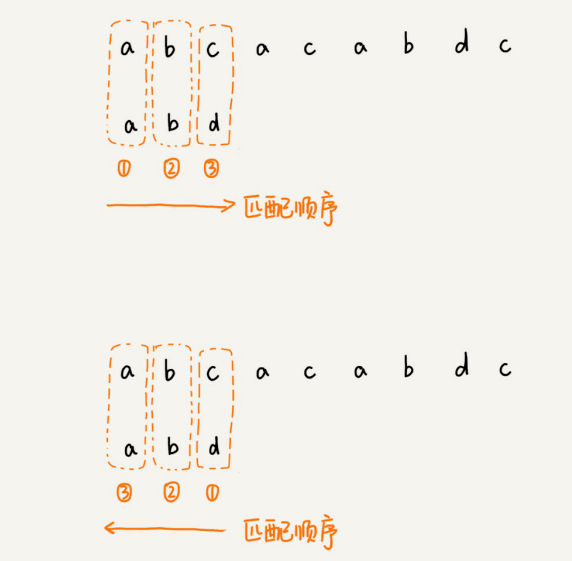
我们从模式串的末尾往前倒着匹配，当我们发现某个字符没法匹配的时候。我们把这个没有匹配的字符叫作坏字符（主串中的字符）。

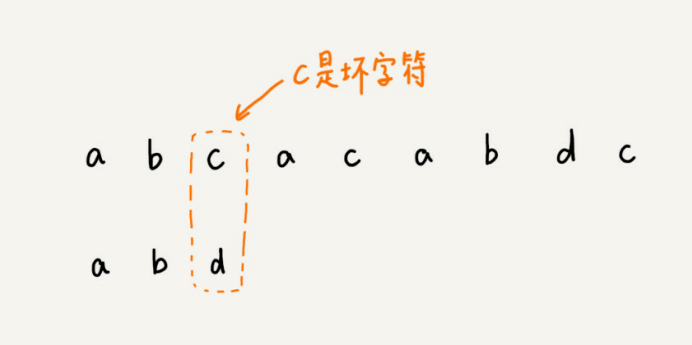
我们拿坏字符c在模式串中查找，发现模式串中并不存在这个字符，也就是说，字符c与模式串中的任何字符都不可能匹配。这个时候，我们可以将模式串直接往后滑动三位，将模式串滑动到c后⾯的位置，再从模式串的末尾字符开始⽐较。

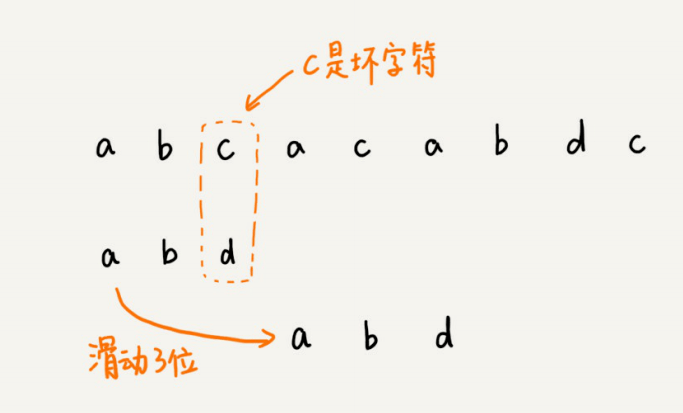
这个时候，我们发现，模式串中最后⼀个字符d，还是⽆法跟主串中的a匹配，这个时候，还能将模式串往后滑动三位吗？答案是不⾏的。因为这个时候，坏字符a在模式串中是存在的，模式串中下标是0的位置也是字符a。这种情况下，我们可以将模式串往后滑动两位，让两个a上下对⻬，然后再从模式串的末尾字符开始，重新匹配。

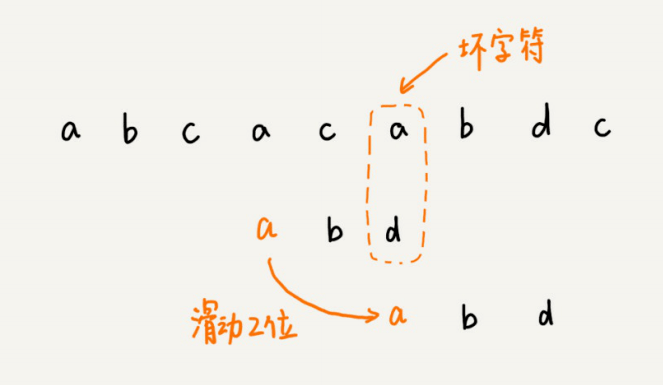
如果坏字符在模式串⾥多处出现，那我们在计算xi的时候，选择最靠后的那个，因为这样不会让模式串滑动过多，导致本来可能匹配的情况被滑动略过。

利⽤坏字符规则，BM算法在最好情况下的时间复杂度⾮常低，是O(n/m)。⽐如，主串是aaabaaabaaabaaab，模式串是aaaa。每次⽐对，模式串都可以直接后移四位，所以，匹配具有类似特点的模式串和主串的时候，BM算法⾮常⾼效。

不过，单纯使⽤坏字符规则还是不够的。因为根据si-xi计算出来的移动位数，有可能是负数，⽐如主串是aaaaaaaaaaaaaaaa，模式串是baaa。不但不会向后滑动模式串，还有可能倒退。所以，BM算法还需要⽤到“好后缀规则”。

2.好后缀规则

好后缀规则实际上跟坏字符规则的思路很类似。当模式串滑动到图中的位置的时候，模式串和主串有2个字符是匹配的，倒数第3个字符发⽣了不匹配的情况。

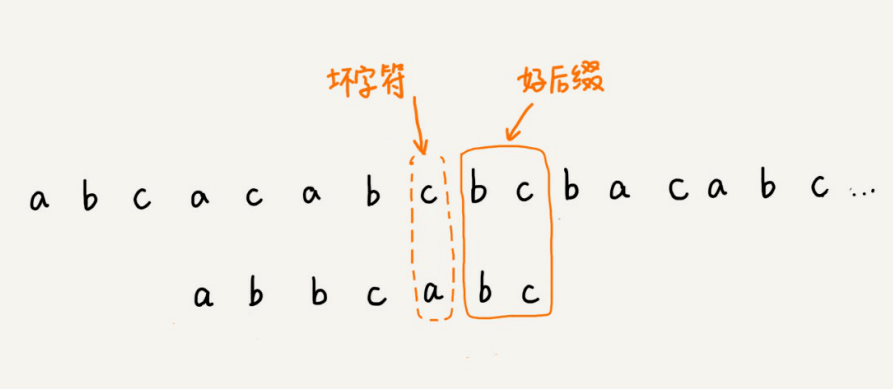
我们把已经匹配的bc叫作好后缀，记作{u}。我们拿它在模式串中查找，如果找到了另⼀个跟{u}相匹配的⼦串{u}，那我们就将模式串滑动到⼦串{u}与主串中{u}对⻬的位置。

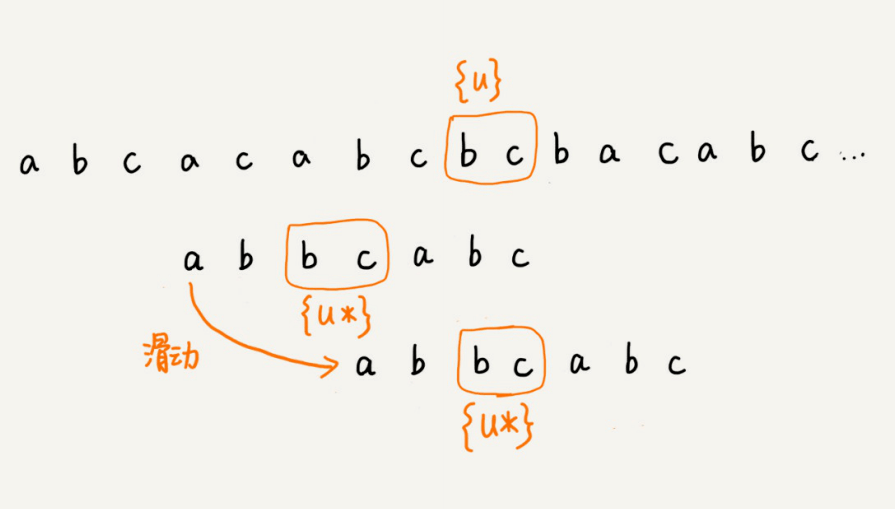
如果在模式串中找不到另⼀个等于{u}的⼦串，我们就直接将模式串，滑动到主串中{u}的后⾯，因为之前的任何⼀次往后滑动，都没有匹配主串中{u}的情况。

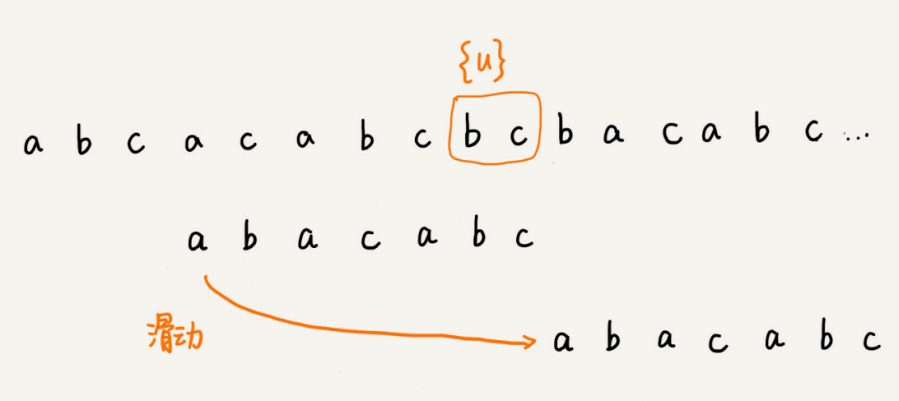
不过，当模式串中不存在等于{u}的⼦串时，我们直接将模式串滑动到主串{u}的后⾯。这样做是否有点太过头呢？我们来看下⾯这个例⼦。这⾥⾯bc是好后缀，尽管在模式串中没有另外⼀个相匹配的⼦串{u*}，但是如果我们将模式串移动到好后缀的后⾯，如图所示，那就会错过模式串和主串可以匹配的情况。

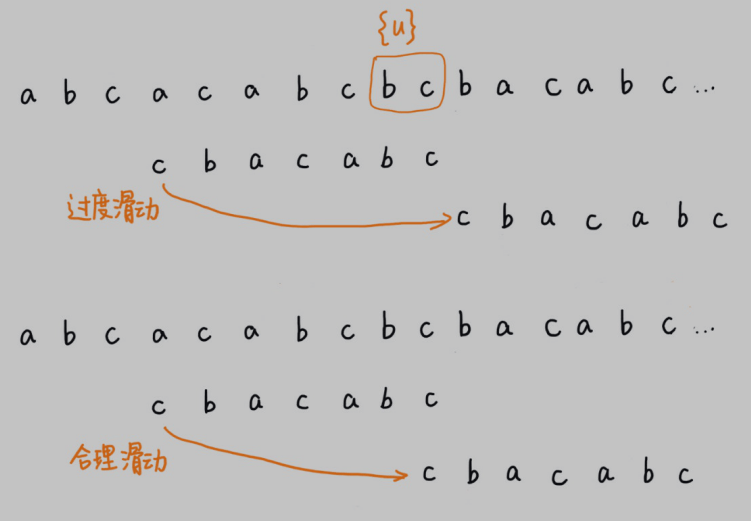
如果好后缀在模式串中不存在可匹配的⼦串，那在我们⼀步⼀步往后滑动模式串的过程中，只要主串中的{u}与模式串有重合，那肯定就⽆法完全匹配。但是当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候，并且重合的部分相等的时候，就有可能会存在完全匹配的情况。

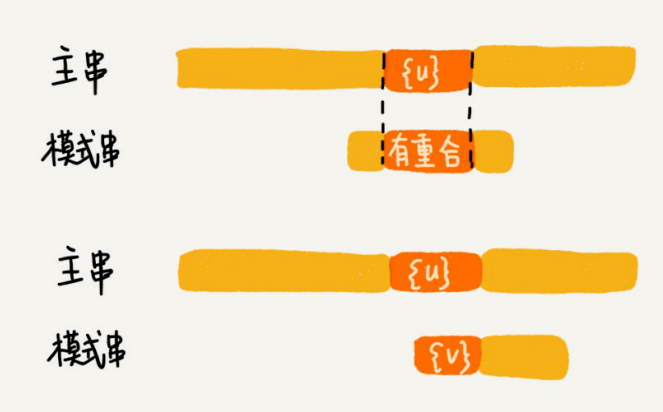
所以，针对这种情况，我们不仅要看好后缀在模式串中，是否有另⼀个匹配的⼦串，我们还要考察好后缀的后缀⼦串，是否存在跟模式串的前缀⼦串匹配的。

所谓某个字符串s的后缀⼦串，就是最后⼀个字符跟s对⻬的⼦串，⽐如abc的后缀⼦串就包括c, bc。所谓前缀⼦串，就是起始字符跟s对⻬的⼦串，⽐如abc的前缀⼦串有a，ab。我们从好后缀的后缀⼦串中，找⼀个最⻓的并且能跟模式串的前缀⼦串匹配的，假设是{v}，然后将模式串滑动到如图所示的位置。

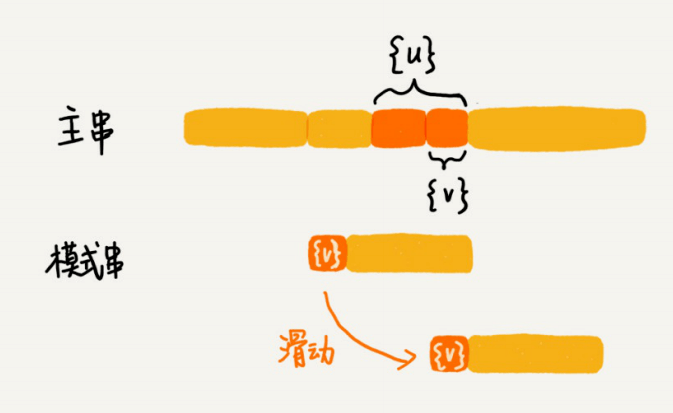
当模式串和主串中的某个字符不匹配的时候，如何选择⽤好后缀规则还是坏字符规则，来计算模式串往后滑动的位数？

我们可以分别计算好后缀和坏字符往后滑动的位数，然后取两个数中最⼤的，作为模式串往后滑动的位数。这种处理⽅法还可以避免我们前⾯提到的，根据坏字符规则，计算得到的往后滑动的位数，有可能是负数的情况。

KMP算法

KMP算法的核⼼思想，跟BM算法⾮常相近。我们假设主串是a，模式串是b。在模式串与主串匹配的过程中，当遇到不可匹配的字符的时候，我们希望找到⼀些规律，可以将模式串往后多滑动⼏位，跳过那些肯定不会匹配的情况。

在模式串和主串匹配的过程中，把不能匹配的那个字符仍然叫作坏字符，把已经匹配的那段字符串叫作好前缀。

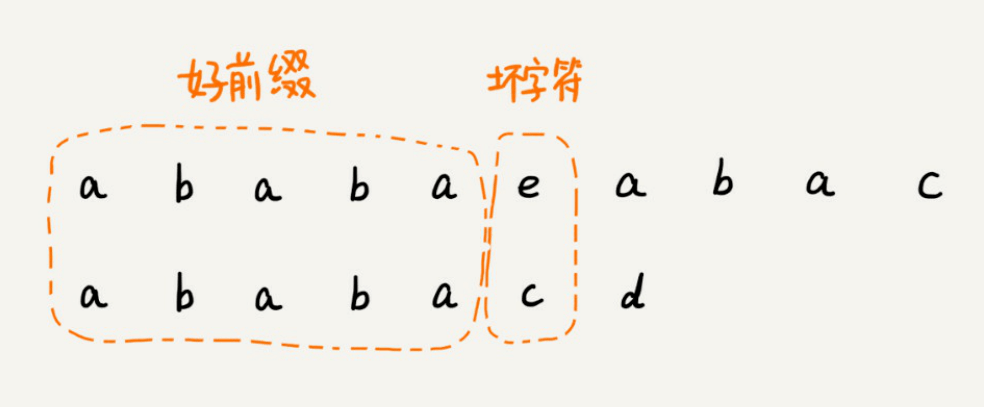
当遇到坏字符的时候，我们就要把模式串往后滑动，在滑动的过程中，只要模式串和好前缀有上下重合，前⾯⼏个字符的⽐较，就相当于拿好前缀的后缀⼦串，跟模式串的前缀⼦串在⽐较。这个⽐较的过程能否更⾼效了呢？可以不⽤⼀个字符⼀个字符地⽐较了吗？

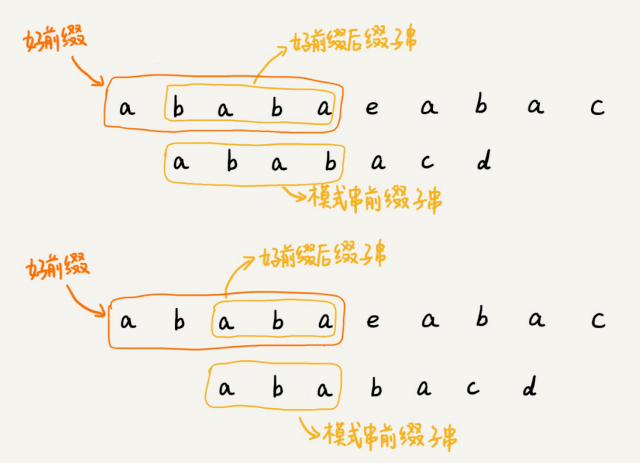
KMP算法就是在试图寻找⼀种规律：在模式串和主串匹配的过程中，当遇到坏字符后，对于已经⽐对过的好前缀，能否找到⼀种规律，将模式串⼀次性滑动很多位？

我们只需要拿好前缀本身，在它的后缀⼦串中，查找最⻓的那个可以跟好前缀的前缀⼦串匹配的。假设最⻓的可匹配的那部分前缀⼦串是{v}，⻓度是k。我们把模式串⼀次性往后滑动j-k位，相当于，每次遇到坏字符的时候，我们就把j更新为k，i不变，然后继续⽐较。

好前缀的所有后缀⼦串中，最⻓的可匹配前缀⼦串的那个后缀⼦串，叫作最⻓可匹配后缀⼦串；对应的前缀⼦串，叫作最⻓可匹配前缀⼦串。

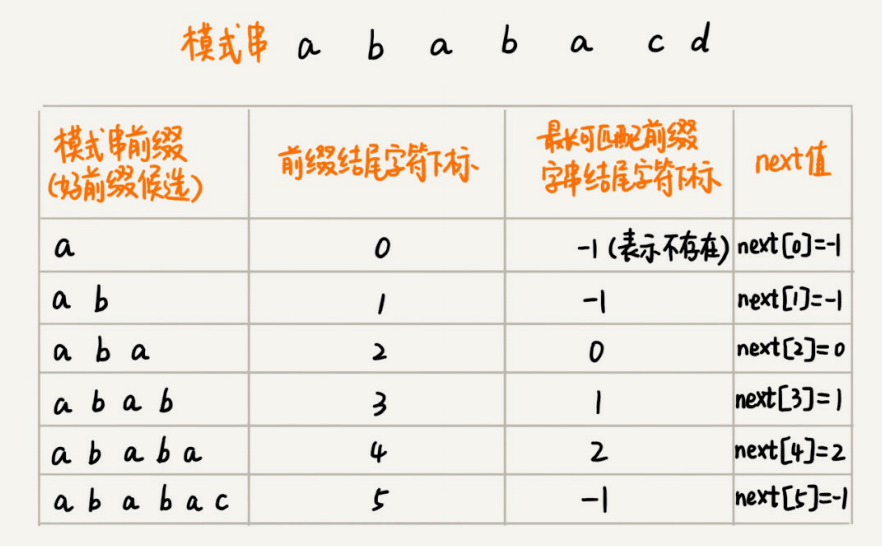
如何来求好前缀的最⻓可匹配前缀和后缀⼦串呢？我发现，这个问题其实不涉及主串，只需要通过模式串本身就能求解。所以，我就在想，能不能事先预处理计算好，在模式串和主串匹配的过程中，直接拿过来就⽤呢？

类似BM算法中的bc、suffifix、prefifix数组，KMP算法也可以提前构建⼀个数组，⽤来存储模式串中每个前缀（这些前缀都有可能是好前缀）的最⻓可匹配前缀⼦串的结尾字符下标。我们把这个数组定义为next数组，很多书中还给这个数组起了⼀个名字，叫失效函数（failure function）。

数组的下标是每个前缀结尾字符下标，数组的值是这个前缀的最⻓可以匹配前缀⼦串的结尾字符下标。

本作品采用《CC 协议》，转载必须注明作者和本文链接