MCMC 方法图像重建理论
二维 MCMC 方法理论
MCMC 法重建图像的主要思路是利用马尔可夫链思想获得转移概率,再利用转移概率进行赋值重建,首先,将二维图形看作一个矩阵,将页岩岩心图像进行二值化,每个点只有0和1两种状态:
- 小于阈值部分代表岩石骨架
- 大于阈值部分代表岩石孔隙
\displaystyle g(x)=\left\{ \begin{aligned} 0,\ \ f(x,y)<阈值\\ 1,\ \ f(x,y)\geqslant阈值 \end{aligned} \right.
引入邻域的思想,认为模型中任何点的状态只取决于相邻少数点的状态。具体地说,就是对于一个特定的点s,用\Lambda_{-s}表示除s外的所有点。则存在一个s点的领域N_s,有
\displaystyle P(x_s|x(\Lambda_{-s}))\approx P(x_s|x(N_s))
对于2点邻域系统,定义影响的某点状态的邻域为该点左边1个点;对于5点邻域系统,定义影响的某点状态的邻域为该点上面的3个点和左边的1个点;对于6点邻域系统,定义影响的某点状态的邻域为该点上面的3个点和左边的2个点。
\displaystyle N_2(i,j)=\left[i,j+1 \right]\\{}\\ N_5(i,j)=\left[\begin{aligned}(i-1,j-1)(i-1,j)\\(i,j-1)(i-1,j+1)\end{aligned}\right]\\{}\\ N_6(i,j+1)=\left[\begin{aligned}(i-1,j-1)(i-1,j)(i-1,j+1)\\(i,j-1)(i,j)\end{aligned}\right]
(i,j) |
(i,j+1) |
(i-1,j-1) |
(i-1,j) |
(i-1,j+1) |
(i,j-1) |
(i,j) |
(i,j+1) |
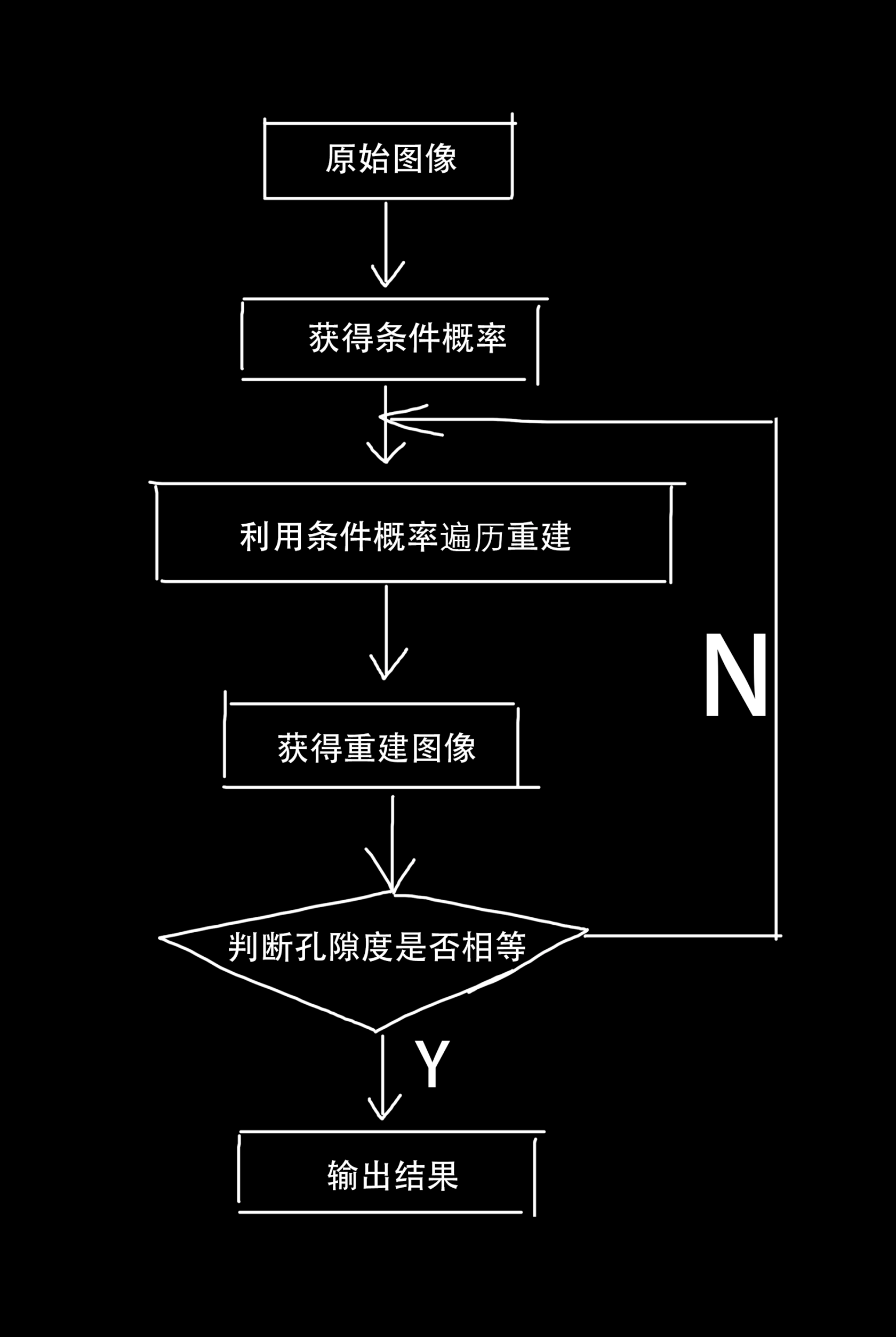
获得条件概率后,就可以利用其为像素赋值,进行图像的重建。重建的步骤为:
-
利用孔隙度确定(1,1)点的状态,然后利用2点邻域模版的条件概率,从左向右依次为(1,j)点赋值。
-
利用孔隙度确定(1,1)点的状态,然后利用2点邻域模版的条件概率,从上往下依次为(i,1)点赋值。
-
利用(1,1)、(1,2)和(2,1)点的状态,采用4点邻域模版的条件概率,对(2,2)赋值;同理,从上往下依次为点(i,j)赋值,其中i>2。
-
采用6点邻域模版,从第2行开始从左向右依次为点(2,j)赋值,到第2行结尾时,采用同样方法对第3行(3,j)赋值,依此类推,直至对最后一行赋值,图像重建结束。
-
对比重构图像与原图的孔隙度,如果达到要求就终止计算,输出最终结果;如果不符合孔隙度要求,则调整条件概率的加权因子,再次开始重构过程,直到符合要求为止。
本作品采用《CC 协议》,转载必须注明作者和本文链接




 关于 LearnKu
关于 LearnKu




博主,您好,请问一下这里是怎么根据领域系统计算条件概率的?