MCMC 法构建三维数字岩心

在三维中，任何的体素点(i,j,k)的联合概率函数可表示为：

\displaystyle P\big(x(v_{ijk})\big)=\prod_{l=0}^i\prod_{m=0}^j\prod_{n=0}^kP\big(x_{lmn}|x_{l-1,m,n},x_{l,m-1,n},x_{l,m,n-1}\big)

式中

\displaystyle V_{LMN}=\left\{(l,m,n),0< l< L, 0< m< M, 0< n< N \right\}

具有L行、M列、N层个正方体体素的长方体网格：
-
(i,j,k)——位于第i行、第j列和第k层体素；
-
x——体素(i,j,k)所处的状态；
-
V_{ijk}——长宽高分别为i、j、k长方体网格；
-
x(V_{ijk})——V_{ijk}的状态。

11点的邻域条件概率和12点邻域条件概率分别写作：

\displaystyle P\bigg(x_{i,j,k}\bigg|x\big(N_{11}(i,j,k)\big)\bigg)=\alpha\left[ \begin{aligned} P(x_{i,j,k}|x(N_{i,5}(i,j,k)))+\\ P(x_{i,j,k}|x(N_{j,6}(i,j,k)))+\\ P(x_{i,j,k}|x(N_{k,5}(i,j,k))) \end{aligned} \right]\\{}\\ P\bigg(x_{i,j+1,k}\bigg|x\big(N_{12}(i,j+1,k)\big)\bigg)=\alpha\left[ \begin{aligned} P(x_{i,j+1,k}|x(N_{i,6}(i,j+1,k)))+\\ P(x_{i,j+1,k}|x(N_{j,6}(i,j+1,k)))+\\ P(x_{i,j+1,k}|x(N_{k,6}(i,j+1,k))) \end{aligned} \right]

其中\alpha为平均化参数，\alpha可由原图测量得到孔隙度和计算重构出的三维介质的孔隙度来确定，概率平均化参数首先由修正系数，通过调价\alpha值可使生成的数字岩心与真实岩心由相同的孔隙度。
对于边界来说，可以用简化的7点、8点、10点、11点邻域来代替11点和12点邻域，比如，若i为2，j为1，那么11点和12点邻域就退化为7点和8点邻域。
利用 MCMC 法构建三维数字岩心的具体步骤：
-
采用岩心扫描图像的孔隙度作为第一个体素状态的条件概率。
-
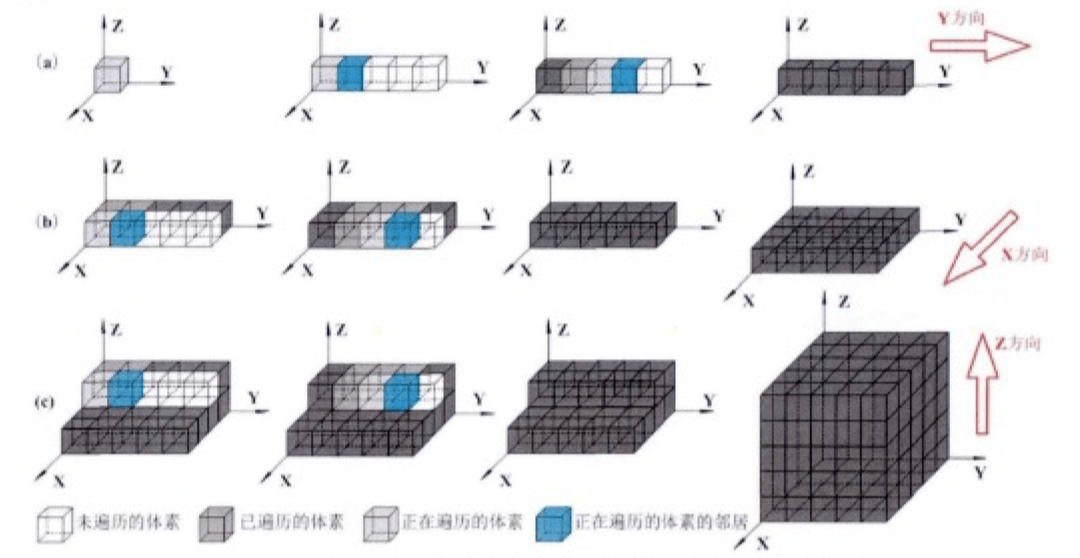
沿y方向生成第一层第一行上的体素。第一行第二个体素使用2邻居进行模拟，之后的体素使用3邻居进行生成。其条件概率由xy平面的岩心扫描图像的6邻域系统进行推导得出。
-
重复步骤，实现X方向各行体素的生成。在边缘体素使用3、4邻居进行模拟，内部体素使用5、6邻居进行模拟。其条件概率由xy平面岩心扫描图像的6邻域系统进行推导得出。
-
重复步骤，实现Z方向各行体素的生成。在边缘体素使用3、4邻居进行模拟，内部体素使用5、6邻居进行模拟，其条件概率由同方向平面的 岩心扫描图像6邻域系统进行推导得出。从第二层第二行开始，边缘体素使用9、10邻居进行模拟，内部体素14、15邻居进行模拟，其条件概率由3个平面岩心扫描图像的6邻域系统组合得到。

算法伪代码：

for i=1 to height
    for j=1 to width
        for k=1 to length
            ConditionalProbabilityMatrix 遍历扫描算法获得概率分布函数
        next k
    next j
next i
for i=1 to height
    for j=1 to width
        for k=1 to length
            generatePoint 根据条件概率给体素点赋值
        next k
    next j
next i

本作品采用《CC 协议》，转载必须注明作者和本文链接