机器学习之简化正则化:L2 正则化

请查看以下泛化曲线, 该曲线显示的是训练集和验证集相对于训练迭代次数的损失.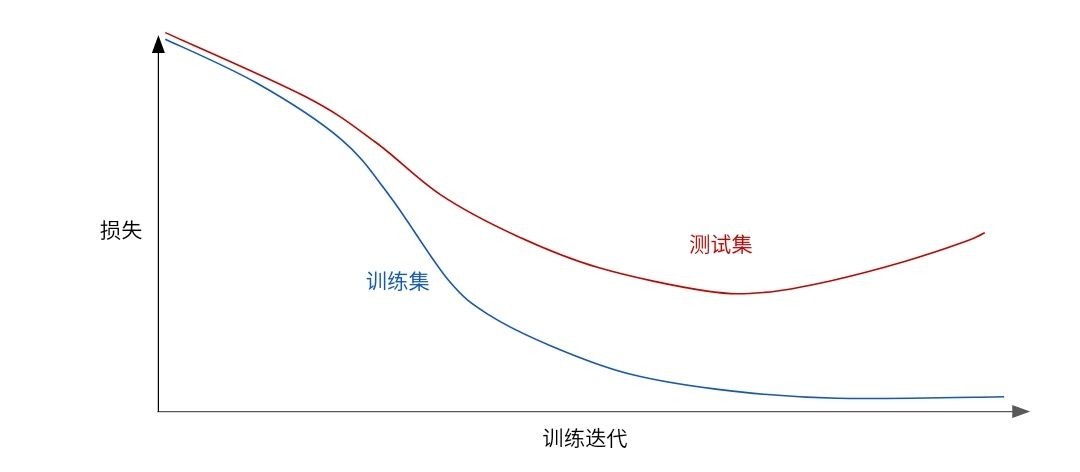

图 1.训练集和验证集损失

图 1 显示的是某个模型的训练损失逐渐减少, 但验证损失最终增加.换言之, 该泛化曲线显示该模型与训练集中的数据过拟合.根据奥卡姆剃刀定律, 或许我们可以通过降低复杂模型的复杂度来防止过拟合, 这种原则称为正则化。
也就是说, 并非只是以最小化损失 ( 经验风险最小化 ) 为目标:

minimize ( Loss ( Data|Model ))

而是以最小化损失和复杂度为目标, 这称为结构风险最小化:

minimize(Loss(Data|Model) + complexity(Model))

现在, 我们的训练优化算法是一个由两项内容组成的函数:一个是损失项, 用于衡量模型与数据的拟合度, 另一个则是正则化项, 用于衡量模型的复杂度。
机器学习速成课程重点介绍了这两种衡量模型复杂度的常见方式 ( 这两种方式有些相关 ):

• 将模型复杂度作为模型中所有特征的权重的函数。
• 将模型复杂度作为具有非零权重的特征总数的函数。
  如果模型复杂度是权重的函数, 则特征权重的绝对值越高, 对模型复杂度的贡献就越大.
  我们可以使用 L₂ 正则化公式来衡量复杂度, 该公式将正则化项定义为所有特征权重的平方和:

  L_2 regularization term = ||w||_{2}^{2} = w_{1}^{2} + w_{2}^{2} + ... +w_{n}^{2}

  在这个公式中, 接近于 0 的权重对模型的复杂度几乎没有影响, 而离群值权重则可能会产生巨大的影响。
  例如, 某个线性模型具有以下权重:

  w_1 = 0.2, w_2 = 0.5, w_3 = 5, w_4 = 2, \\w_5 = 0.25, w_6 = 0.75

L_2 正则化项为 26.915:

w_{1}^{2} + w_{2}^{2} + \mathbf{w_{3}^{2}} + w_{4}^{2} + w_{5}^{2 }+ w_{6}^{2}\\ = 0.2^{2} + 0.5^{2} + \mathbf{5^{2}} + 1^{2} + 0.25^{2} + 0.75^{2}\\ = 0.04 + 0.25 + \mathbf{25} + 1 + 0.0625 + 0.5625 = 26.915

但是w_3( 上述加粗内容 ) 的平方值为 25， 几乎贡献了全部的复杂度。所有 5 个其他权重的平方和对 L_2 正则化的贡献仅为 1.915.

本作品采用《CC 协议》，转载必须注明作者和本文链接