机器学习之逻辑回归：计算概率

许多问题需要将概率估算值作为输出。逻辑回归是一种极其高效的概率计算机制。实际上， 您可以通过下两种方式之一使用返回概率：

• “按原样”
• 转换成二元类别。
  我们来了解一下如何“按原样”使用概率。假设我们创建一个逻辑回归模型来预测狗在半夜发出叫声的概率。我们将此概率称为：

  p ( bark | night )

  如果逻辑回归模型预测 p ( bark | night ) 的值为 0.05，那么一年内， 狗的主人应该被叫醒约 18 次：

  startled = p( bark | night ) *nights
  18 ~= 0.05 * 365

  在很多情况下， 您会将逻辑回归输出映射到二元分类问题的解决方案， 该二元分类问题的目标是正确预测两个可能的标签 （ 例如，“垃圾邮件” 或 “非垃圾邮件” ）中的一个。
  您可能想知道逻辑回归问题模型如何确保输出值始终落在 0 和 1 之间。巧合的是，S 型函数生成的输出值正好具有这些特征，其定义如下：

  y = \dfrac{1}{1 + e^{-z}}

  S 型函数会产生以下曲线图：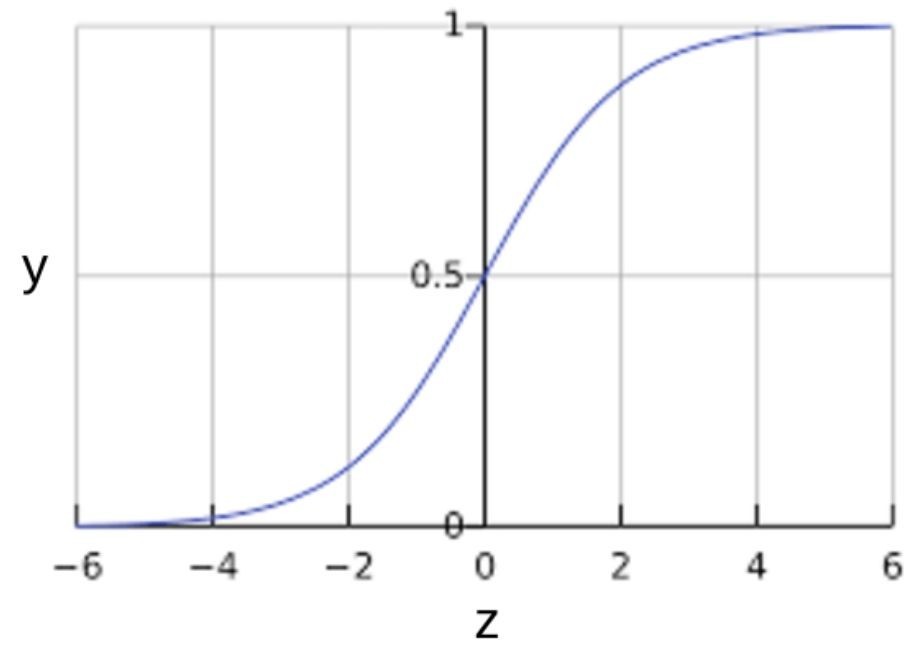
  

  图 1: S 型函数

  如果 z 表示使用逻辑回归训练的模型的线性层的输出，则 S 型 ( z ) 函数会生成一个介于 0 和 1 之间的值（ 概率 ）。用数学方法表示为

  y' = \dfrac{1}{1 + e^{-(z)}}

  其中：
• y' 是逻辑回归模型针对特定样本的输出。
• z 是

  b + w_1x_1 + w_1x_2 + ...w_Nx_N

  • w 的值是模型学习的权重，b 是偏差
  • x 的值是特定样本的特征值
    请注意，z 也称为对数几率，因为 S 型函数的反函数表明，z 可定义为标签“1” （ 例如“狗叫”）的概率除以标签“0”（ 例如“狗不叫”）的概率得出的值的对数：

    z = log_{10}(\dfrac{y}{1-y})

    以下是具有机器学习标签的 S 型函数：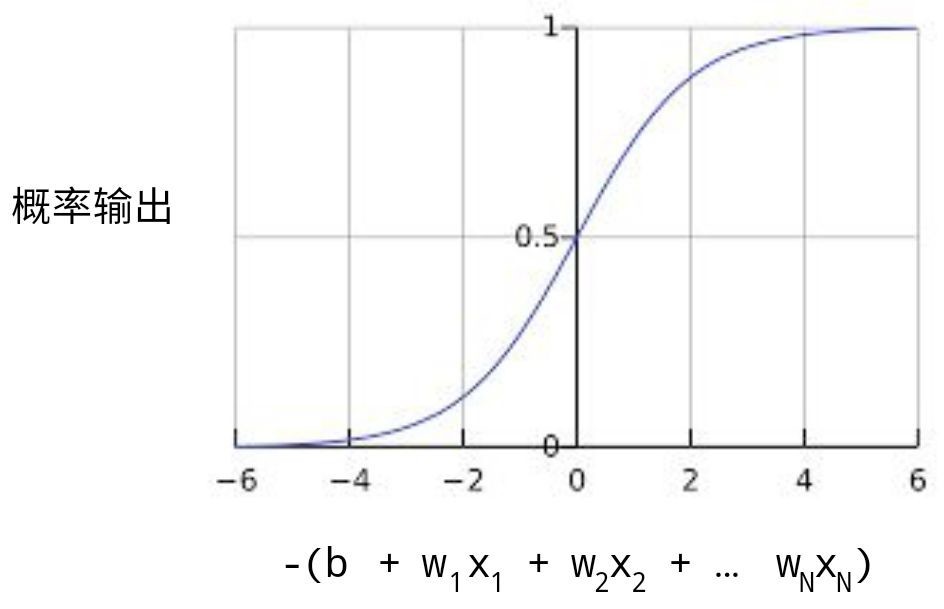
    

本作品采用《CC 协议》，转载必须注明作者和本文链接