机器学习之分类:预测偏差
逻辑回归预测应当无偏差。即:“预测平均值”应当约等于“观察平均值”
预测偏差指的是这两个平均值之间的差值。即:
预测偏差 = 预测平均值 - 数据集中相应标签的平均值
注意:“预测偏差”与“偏差”(“wx + b”中的“b”)不是一回事。
如果出现非常高的非零预测偏差,则说明模型某处存在错误,因为这表明模型对正类别标签的出现频率预测有误。
例如,假设我们知道,所有电子邮件中平均有 1% 的邮件是垃圾邮件。如果我们对某一封给定电子邮件一无所知,则预测它是垃圾邮件的可能性为 1%。同样,一个出色的垃圾邮件模型应该预测到电子邮件平均有 1% 的可能性是垃圾邮件。(换言之,如果我们计算单个电子邮件是垃圾邮件的预测可能性的平均值,则结果应该是 1%。)然而,如果该模型预测电子邮件是垃圾邮件的平均可能性为 20%,那么我们可以得出结论,该模型出现了预测偏差。
造成预测偏差的可能原因包括:
- 特征集不完整
- 数据集混乱
- 模型实现流水线中有错误?
- 训练样本有偏差
- 正则化过强
您可能会通过对学习模型进行后期处理来纠正预测偏差,即通过添加校准层来调整模型的输出,从而减小预测偏差值。例如,如果您的模型存在 3%以上的偏差,则可以添加一个校准层,将平均预测偏差降低 3%。但是,添加校准层并非良策,具体原因如下: - 您修复的是症状,而不是原因。
- 您建立了一个更脆弱的系统,并且必须持续更新。
如果可能的话,请避免添加校准层。使用校准层的项目往往会对其产生依赖 — 使用校准层来修复模型的所有错误。最终,维护校准层可能会令人苦不堪言。
注意:出色模型的偏差通常接近于零。即便如此,预测偏差低并不能证明您的模型比较出色。特别糟糕的模型的预测偏差也有可能为零。例如,只能预测所有样本平均值的模型是糟糕的模型,尽管其预测偏差为零。分桶偏差和预测偏差
逻辑回归可预测 0 到 1 之间的值。不过,所有带标签样本都正好是 0 (例如,0 表示“非垃圾邮件”)或 1 (例如,1 表示“垃圾邮件”)。因此,在检查预测偏差时,您无法仅根据一个样本准确地确定预测偏差;您必须在“一大桶”样本中检查预测偏差。也就是说,只有将足够的样本组合在一起以便能够比较预测值(例如 0.392)与观察值(例如 0.394),逻辑回归的预测偏差才有意义。
您可以通过以下方式构建桶: - 以线性方式分解目标预测
- 构建分位数。
请查看以下某个特定模型的校准曲线。每个点表示包含 1000 个值的分桶。两个轴具有以下含义: - x 轴表示模型针对该桶预测的平均值。
- y 轴表示该桶的数据集中的实际平均值。
两个轴均采用对数尺度。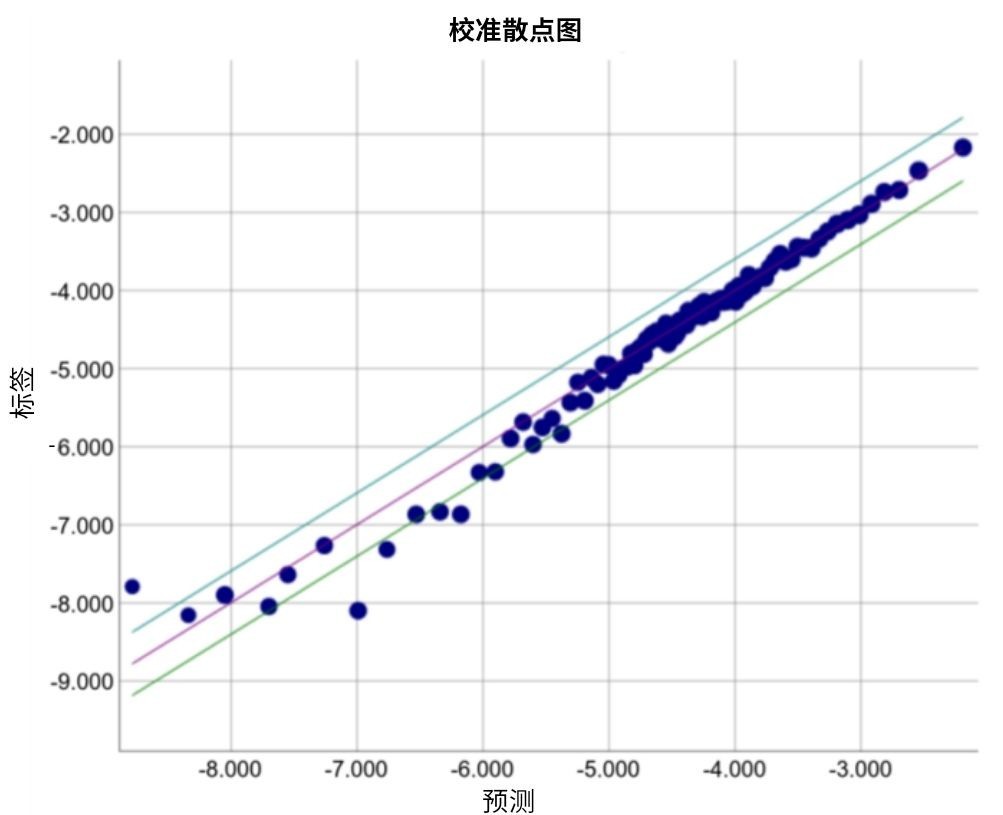
图 8.预测偏差曲线(对数尺度)
为什么只有模型的某些部分所做的预测如此糟糕?以下是几种可能性: - 训练集不能充分表示数据空间的某些子集。
- 数据集的某些子集比其他子集更混乱。
- 该模型过于正则化。(不妨减小 lambda 的值)
本作品采用《CC 协议》,转载必须注明作者和本文链接

 Lois 的个人博客
Lois 的个人博客


 关于 LearnKu
关于 LearnKu



