机器学习之支持向量机（线性模型）的优化问题

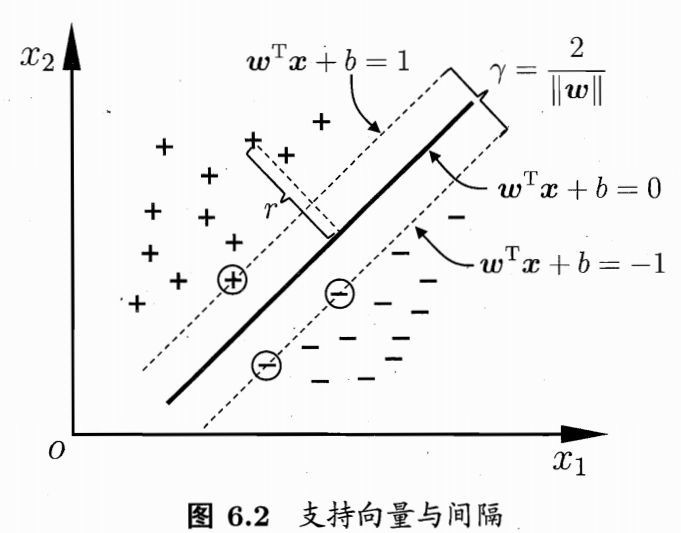
将中间的这条线分别向两边平行移动，直到穿过某一个或某几个训练样本点为止。
我们将超平面记为（W, b)。
定义：
1.训练数据及标签(X_1,y_1) (X_2,y_2)…(X_N,y_N)，其中 X_i 为向量，y_i = + 1或-1
2.一个训练集线性可分是指

训练集：{(X_i,y_i)}_{i = 1\sim N}\\ \exists (\mathbf W,b),使：\\ 对\forall i = 1\sim N,有\\ (1).若 y_i = +1,则 W^TX_i + b\geq 0\\ (2).若 y_i = -1,则W^TX_i + b< 0\\ “(1) 和 (2)”等价于“ y_i[W^TX_i + b]\geq0(公式 1 ) ”

3.支持向量：在支持向量机中，距离超平面最近的且满足一定条件的几个训练样本点被成为支持向量。

支持向量机的优化问题

归结为以下两点：

最小化 ( Minimize ):\dfrac{1}{2}||W||^2

限制条件 ( Subject to ):y_i[W^TX_i + b]\geq 1 ( i = 1\sim N )

证明：
事实 1:w^TX + b = 0 与 aW^TX + ab = 0是同一个平面。a\in R^+
若（W, b）满足公式 1，则(aW, ab) 也满足公式 1。
事实 2:点到平面的距离公式
平面：w_1x + w^2y + b = 0 则(x_0, y_0) 到此平面的距离：

d = \dfrac{|w_1X_0 + w_2y_0 + b|} {\sqrt{w_1^2 + w_2^2}}

支持向量X_0 到超平面 ( W, b ) 的距离可写为

d = \dfrac{|\mathbf{W}^T\mathbf{X_0} +b|}{||\mathbf{W}||}\\ 注意：||W|| = \sqrt {W_1^2 + W_2^2 +... + W_n^2}

我们可以用 a 去缩放

( W, b)\xrightarrow{} ( aW, ab)

最终使在支持向量x_0（所有支持向量上都满足）上有|W^TX_0 + b|=1, 此时支持向量与平面的距离

d = \dfrac{1}{||W||}

所以要使距离\dfrac{2}{||W||}最大化，即最小化\dfrac{1}{2}||W||^2

本作品采用《CC 协议》，转载必须注明作者和本文链接