算法学习之旅,终点亦是起点
可点击右方查看目录
数据结构
脑图:naotu.baidu.com/file/0a53d3a5343bd...
一维:
基础:数组 array (string), 链表 linked list
高级:栈 stack, 队列 queue, 双端队列 deque, 集合 set, 映射 map (hash or map), etc
二维:
基础:树 tree, 图 graph
高级:二叉搜索树 binary search tree (red-black tree, AVL), 堆 heap, 并查集 disjoint set, 字典树 Trie, etc
特殊:
位运算 Bitwise, 布隆过滤器 BloomFilter
LRU Cache
时间复杂度
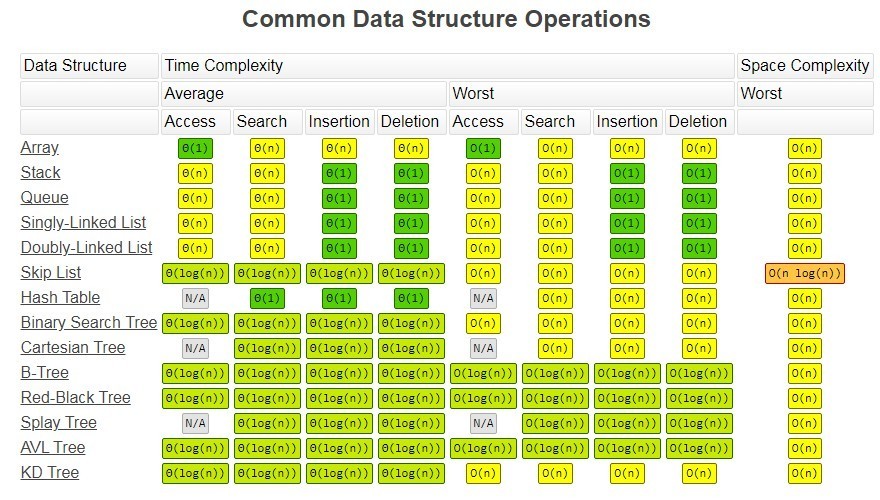
算法
If-else, switch —> branch
for, while loop —> Iteration
递归 Recursion (Divide & Conquer, Backtrace)
搜索 Search: 深度优先搜索 Depth first search, 广度优先搜索 Breadth first search, A*, etc
动态规划 Dynamic Programming
二分查找 Binary Search
贪心 Greedy
数学 Math , 几何 Geometry
刷题路线分享
基础
- 两数之和(简单)
- 有效的括号(简单)
- 字符串解码(中等)
- LRU 缓存机制(困难)
- 实现 Trie(前缀树)(中等)
- 添加与搜索单词 - 数据结构设计(中等)
- 单词搜索 II (困难)
- 找不同(简单)
- 单词规律(简单)
- 字符串中的第一个唯一字符(简单)
- 无重复字符的最长子串(中等)
- 最小覆盖子串(困难)
- 合并两个有序链表(简单)
- 环形链表(简单)
- 环形链表 II (中等)
- 反转链表(简单)
- 反转链表 II (中等)
- 旋转链表(中等)
- 排序链表
- 链表中倒数第 k 个节点
- 两两交换链表中的节点(中等)
- 按奇偶排序数组(简单)
- 按奇偶排序数组 II (简单)
- 有序数组的平方(简单)
- 山脉数组的峰顶索引(简单)
- 搜索旋转排序数组(困难)
- 搜索旋转排序数组 II (中等)
- 寻找旋转排序数组中的最小值(中等)
- 寻找旋转排序数组中的最小值 II (困难)
- 搜索二维矩阵(中等)
- 等式方程的可满足性(中等)
- 朋友圈(中等)
- 账户合并(中等)
深度优先搜索
回溯
分治
动态规划
- 使用最小花费爬楼梯(简单)
- 爬楼梯(简单)
- 不同路径(简单)
- 最小路径和 (中等)
- 最大子序和 (简单)
- 乘积最大子数组(中等)
- 买卖股票的最佳时机(简单)
- 买卖股票的最佳时机 II (简单)
- 买卖股票的最佳时机 III (困难)
- 买卖股票的最佳时机 IV (困难)
- 最佳买卖股票时机含冷冻期(中等)
- 买卖股票的最佳时机含手续费(中等)
- 零钱兑换 (中等)
- 零钱兑换 II (中等)
- 编辑距离(困难)
- 不同的子序列(困难)
- 柱状图中最大的矩形(困难)
- 最大矩形(困难)
- 最大正方形(中等)
- 最低票价(中等)
- 区域和检索 - 数组不可变(简单)
- 二维区域和检索 - 矩阵不可变(中等)
- 最长上升子序列 (中等)
- 鸡蛋掉落(困难)
部分代码模板 (仅供参考)
并不是题目答案,只是说明大部分题目有套路可循;主要是java、python的版本,或者伪代码,应该能看懂。
递归
// java
public void recur(int level, int param) {
// terminator
if (level > MAX_LEVEL) {
// process result
return;
}
// process current logic
process(level, param);
// drill down
recur( level: level + 1, newParam);
// restore current status
}
分治、回溯
// java
private static int divide_conquer(Problem problem, ) {
if (problem == NULL) {
int res = process_last_result();
return res;
}
subProblems = split_problem(problem)
res0 = divide_conquer(subProblems[0])
res1 = divide_conquer(subProblems[1])
result = process_result(res0, res1);
return result;
}
DFS
递归写法
// java
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> allResults = new ArrayList<>();
if(root==null){
return allResults;
}
travel(root,0,allResults);
return allResults;
}
private void travel(TreeNode root,int level,List<List<Integer>> results){
if(results.size()==level){
results.add(new ArrayList<>());
}
results.get(level).add(root.val);
if(root.left!=null){
travel(root.left,level+1,results);
}
if(root.right!=null){
travel(root.right,level+1,results);
}
}
非递归写法
# Python
def DFS(self, tree):
if tree.root is None:
return []
visited, stack = [], [tree.root]
while stack:
node = stack.pop()
visited.add(node)
process (node)
nodes = generate_related_nodes(node)
stack.push(nodes)
# other processing work
...
BFS
# Python
def BFS(graph, start, end):
visited = set()
queue = []
queue.append([start])
while queue:
node = queue.pop()
visited.add(node)
process(node)
nodes = generate_related_nodes(node)
queue.push(nodes)
# other processing work
...
贪心算法
贪心算法是在当前情况下做出的最优决定,它只考虑眼前,获得的是局部的最优解,并且,希望通过每次获得局部最优解最后找到全局的最优解。
二分查找
// Java
public int binarySearch(int[] array, int target) {
int left = 0, right = array.length - 1, mid;
while (left <= right) {
mid = (right - left) / 2 + left;
if (array[mid] == target) {
return mid;
} else if (array[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
动态规划
动态规划 和 递归或者分治 没有根本上的区别(关键看有无最优的子结构)
共性:找到重复子问题
差异性:最优子结构、中途可以淘汰次优解
DP顺推模板
# 伪代码
function DP():
dp = [][] # 二维情况
for i = 0 .. M {
for j = 0 .. N {
dp[i][j] = _Function(dp[i’][j’]...)
}
}
return dp[M][N];
Trie 树(字典树)
// java
class Trie {
private boolean isEnd;
private Trie[] next;
/** Initialize your data structure here. */
public Trie() {
isEnd = false;
next = new Trie[26];
}
/** Inserts a word into the trie. */
public void insert(String word) {
if (word == null || word.length() == 0) return;
Trie curr = this;
char[] words = word.toCharArray();
for (int i = 0;i < words.length;i++) {
int n = words[i] - 'a';
if (curr.next[n] == null) curr.next[n] = new Trie();
curr = curr.next[n];
}
curr.isEnd = true;
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
Trie node = searchPrefix(word);
return node != null && node.isEnd;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
Trie node = searchPrefix(prefix);
return node != null;
}
private Trie searchPrefix(String word) {
Trie node = this;
char[] words = word.toCharArray();
for (int i = 0;i < words.length;i++) {
node = node.next[words[i] - 'a'];
if (node == null) return null;
}
return node;
}
}
并查集
// java
class UnionFind {
private int count = 0;
private int[] parent;
public UnionFind(int n) {
count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
public int find(int p) {
while (p != parent[p]) {
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootP] = rootQ;
count--;
}
}
布隆过滤器
// java
public class BloomFilter {
private static final int DEFAULT_SIZE = 2 << 24;
private static final int[] seeds = new int[] { 5, 7, 11, 13, 31, 37, 61 };
private BitSet bits = new BitSet(DEFAULT_SIZE);
private SimpleHash[] func = new SimpleHash[seeds.length];
public BloomFilter() {
for (int i = 0; i < seeds.length; i++) {
func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
}
}
public void add(String value) {
for (SimpleHash f : func) {
bits.set(f.hash(value), true);
}
}
public boolean contains(String value) {
if (value == null) {
return false;
}
boolean ret = true;
for (SimpleHash f : func) {
ret = ret && bits.get(f.hash(value));
}
return ret;
}
// 内部类,simpleHash
public static class SimpleHash {
private int cap;
private int seed;
public SimpleHash(int cap, int seed) {
this.cap = cap;
this.seed = seed;
}
public int hash(String value) {
int result = 0;
int len = value.length();
for (int i = 0; i < len; i++) {
result = seed * result + value.charAt(i);
}
return (cap - 1) & result;
}
}
}
LRU Cache
// java 哈希表 + 双链表
class LRUCache {
/**
* 缓存映射表
*/
private Map<Integer, DLinkNode> cache = new HashMap<>();
/**
* 缓存大小
*/
private int size;
/**
* 缓存容量
*/
private int capacity;
/**
* 链表头部和尾部
*/
private DLinkNode head, tail;
public LRUCache(int capacity) {
//初始化缓存大小,容量和头尾节点
this.size = 0;
this.capacity = capacity;
head = new DLinkNode();
tail = new DLinkNode();
head.next = tail;
tail.prev = head;
}
/**
* 获取节点
* @param key 节点的键
* @return 返回节点的值
*/
public int get(int key) {
DLinkNode node = cache.get(key);
if (node == null) {
return -1;
}
//移动到链表头部
(node);
return node.value;
}
/**
* 添加节点
* @param key 节点的键
* @param value 节点的值
*/
public void put(int key, int value) {
DLinkNode node = cache.get(key);
if (node == null) {
DLinkNode newNode = new DLinkNode(key, value);
cache.put(key, newNode);
//添加到链表头部
addToHead(newNode);
++size;
//如果缓存已满,需要清理尾部节点
if (size > capacity) {
DLinkNode tail = removeTail();
cache.remove(tail.key);
--size;
}
} else {
node.value = value;
//移动到链表头部
moveToHead(node);
}
}
/**
* 删除尾结点
*
* @return 返回删除的节点
*/
private DLinkNode removeTail() {
DLinkNode node = tail.prev;
removeNode(node);
return node;
}
/**
* 删除节点
* @param node 需要删除的节点
*/
private void removeNode(DLinkNode node) {
node.next.prev = node.prev;
node.prev.next = node.next;
}
/**
* 把节点添加到链表头部
*
* @param node 要添加的节点
*/
private void addToHead(DLinkNode node) {
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
/**
* 把节点移动到头部
* @param node 需要移动的节点
*/
private void moveToHead(DLinkNode node) {
removeNode(node);
addToHead(node);
}
/**
* 链表节点类
*/
private static class DLinkNode {
Integer key;
Integer value;
DLinkNode prev;
DLinkNode next;
DLinkNode() {
}
DLinkNode(Integer key, Integer value) {
this.key = key;
this.value = value;
}
}
}
十大经典排序算法
阅读:www.cnblogs.com/onepixel/p/7674659...
图片来源于上文
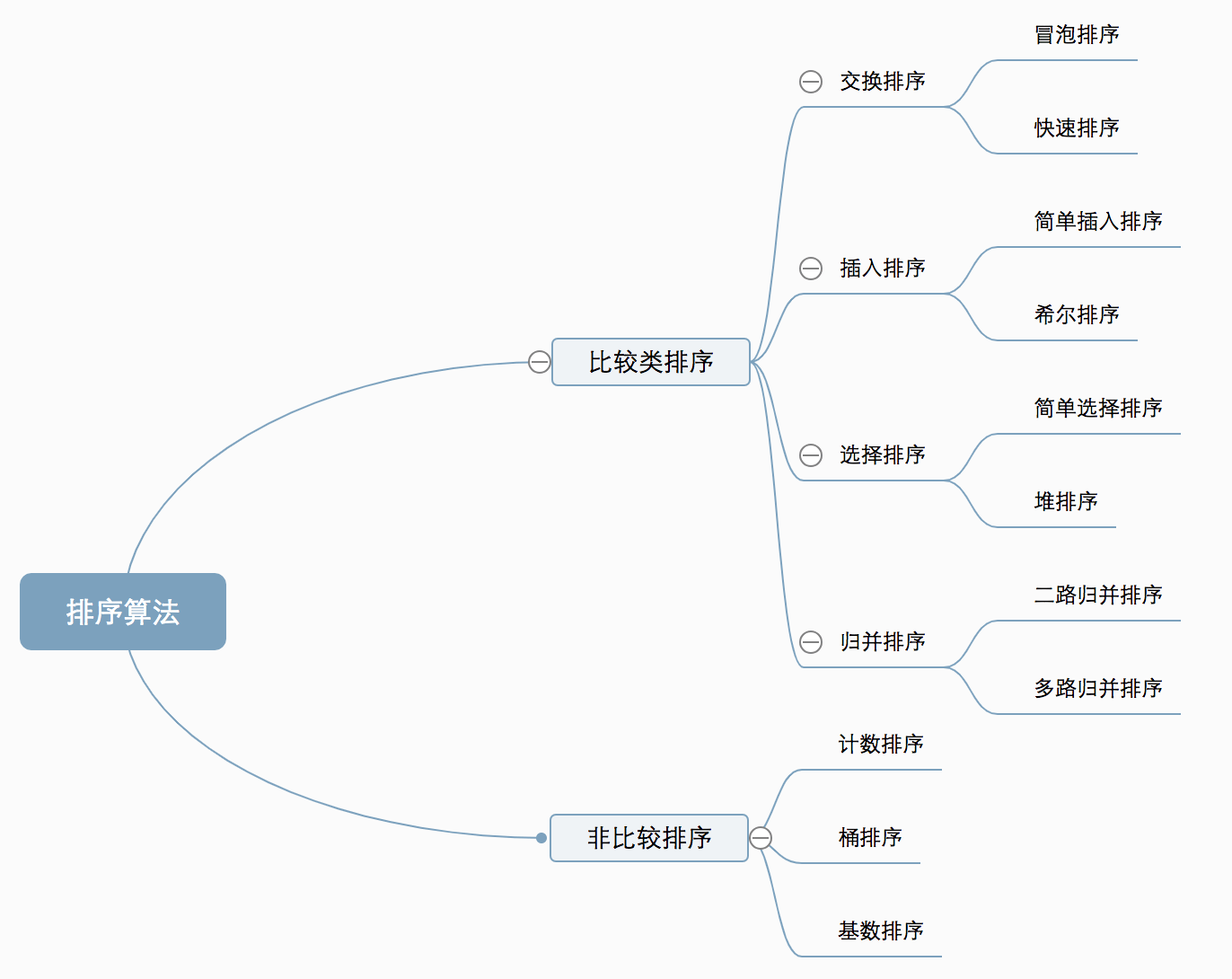
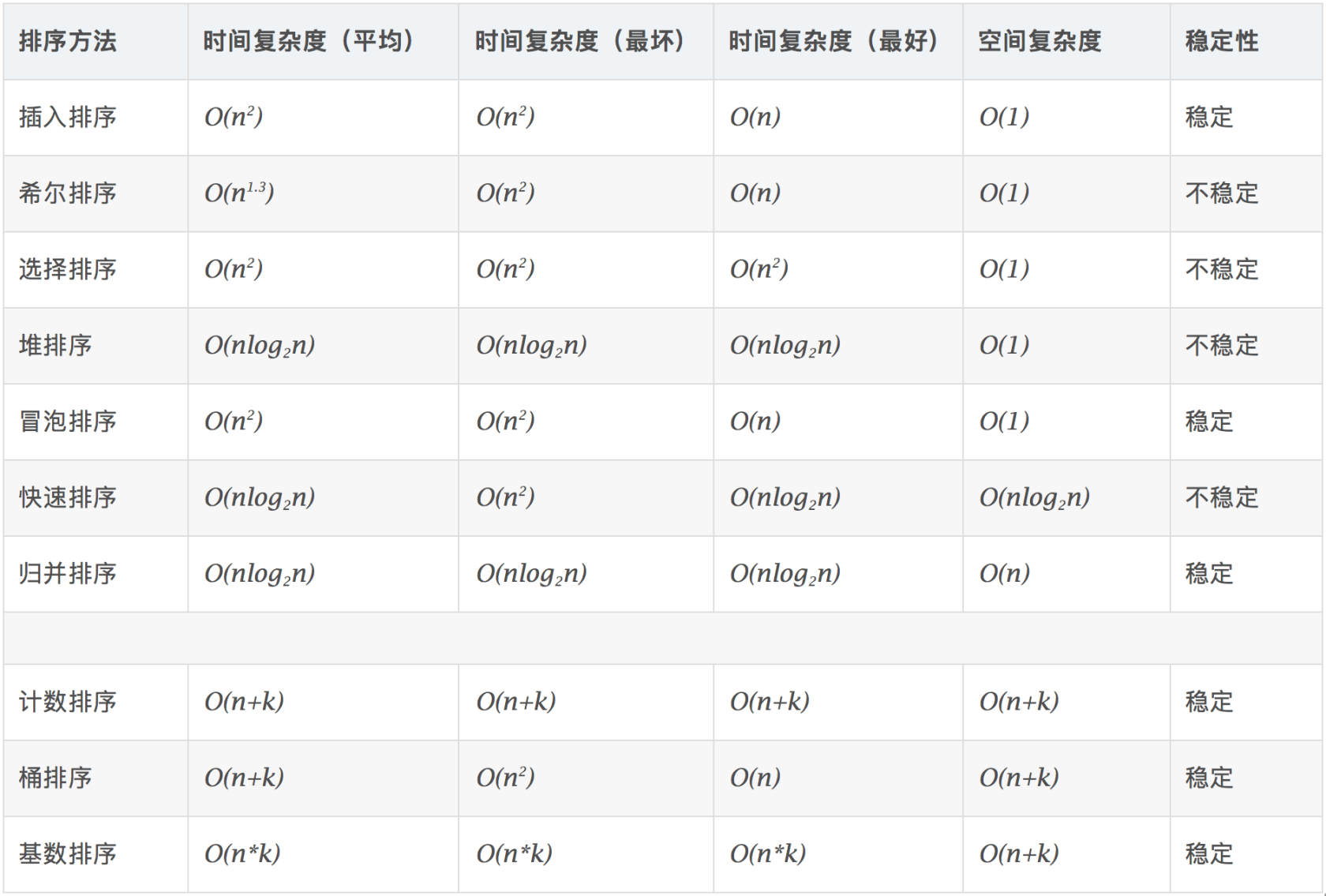
快速排序
// java
public static void quickSort(int[] array, int begin, int end) {
if (end <= begin) return;
int pivot = partition(array, begin, end);
quickSort(array, begin, pivot - 1);
quickSort(array, pivot + 1, end);
}
static int partition(int[] a, int begin, int end) {
// pivot: 标杆位置,counter: 小于pivot的元素的个数
int pivot = end, counter = begin;
for (int i = begin; i < end; i++) {
if (a[i] < a[pivot]) {
int temp = a[counter]; a[counter] = a[i]; a[i] = temp;
counter++;
}
}
int temp = a[pivot]; a[pivot] = a[counter]; a[counter] = temp;
return counter;
}
归并排序
// java
public static void mergeSort(int[] array, int left, int right) {
if (right <= left) return;
int mid = (left + right) >> 1; // (left + right) / 2
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
merge(array, left, mid, right);
}
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1]; // 中间数组
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
}
while (i <= mid) temp[k++] = arr[i++];
while (j <= right) temp[k++] = arr[j++];
for (int p = 0; p < temp.length; p++) {
arr[left + p] = temp[p];
}
// 也可以用 System.arraycopy(a, start1, b, start2, length)
}
堆排序
// java
public static void heapSort(int[] array) {
if (array.length == 0) return;
int length = array.length;
for (int i = length / 2-1; i >= 0; i-)
heapify(array, length, i);
for (int i = length - 1; i >= 0; i--) {
int temp = array[0]; array[0] = array[i]; array[i] = temp;
heapify(array, i, 0);
}
}
static void heapify(int[] array, int length, int i) {
int left = 2 * i + 1, right = 2 * i + 2;
int largest = i;
if (left < length && array[left] > array[largest]) {
largest = left;
}
if (right < length && array[right] > array[largest]) {
largest = right;
}
if (largest != i) {
int temp = array[i]; array[i] = array[largest]; array[largest] = temp;
heapify(array, length, largest);
}
}结语
光说不练假把式,重要的是动手做题。
本作品采用《CC 协议》,转载必须注明作者和本文链接






 关于 LearnKu
关于 LearnKu




巨佬巨佬
整挺好