数据结构之堆(Heap)
堆的构建、插入、取出
一.堆的定义:
堆(heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
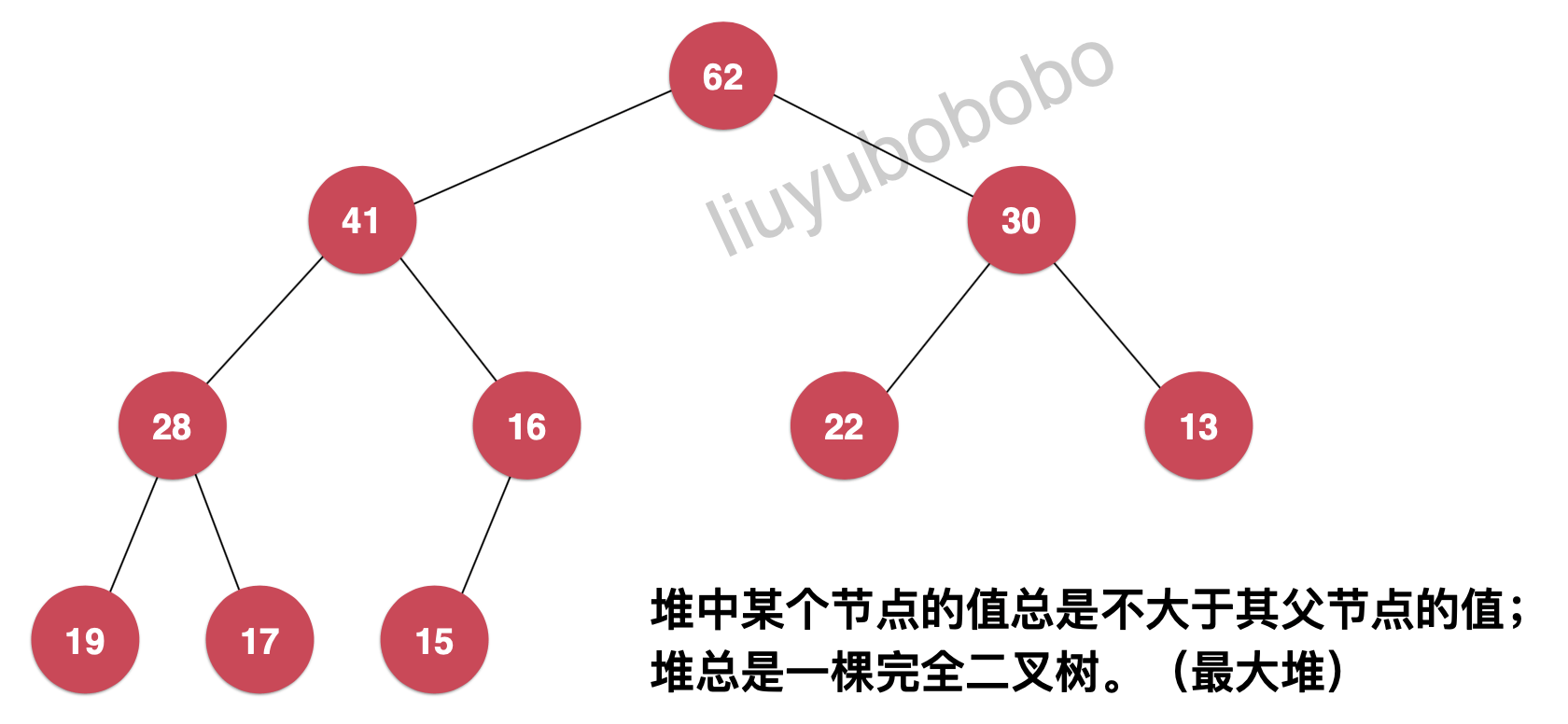
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。
将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、[斐波那契堆]等。
堆是非线性数据结构,相当于一维数组,有两个直接后继。
二. 逻辑:
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。有如下事实:
Ki >= K(2i),Ki >= K(i+1)或者Ki <= K(2i),Ki <= K(i+1)
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
这里我们以最大堆为例进行讲解,如下图:

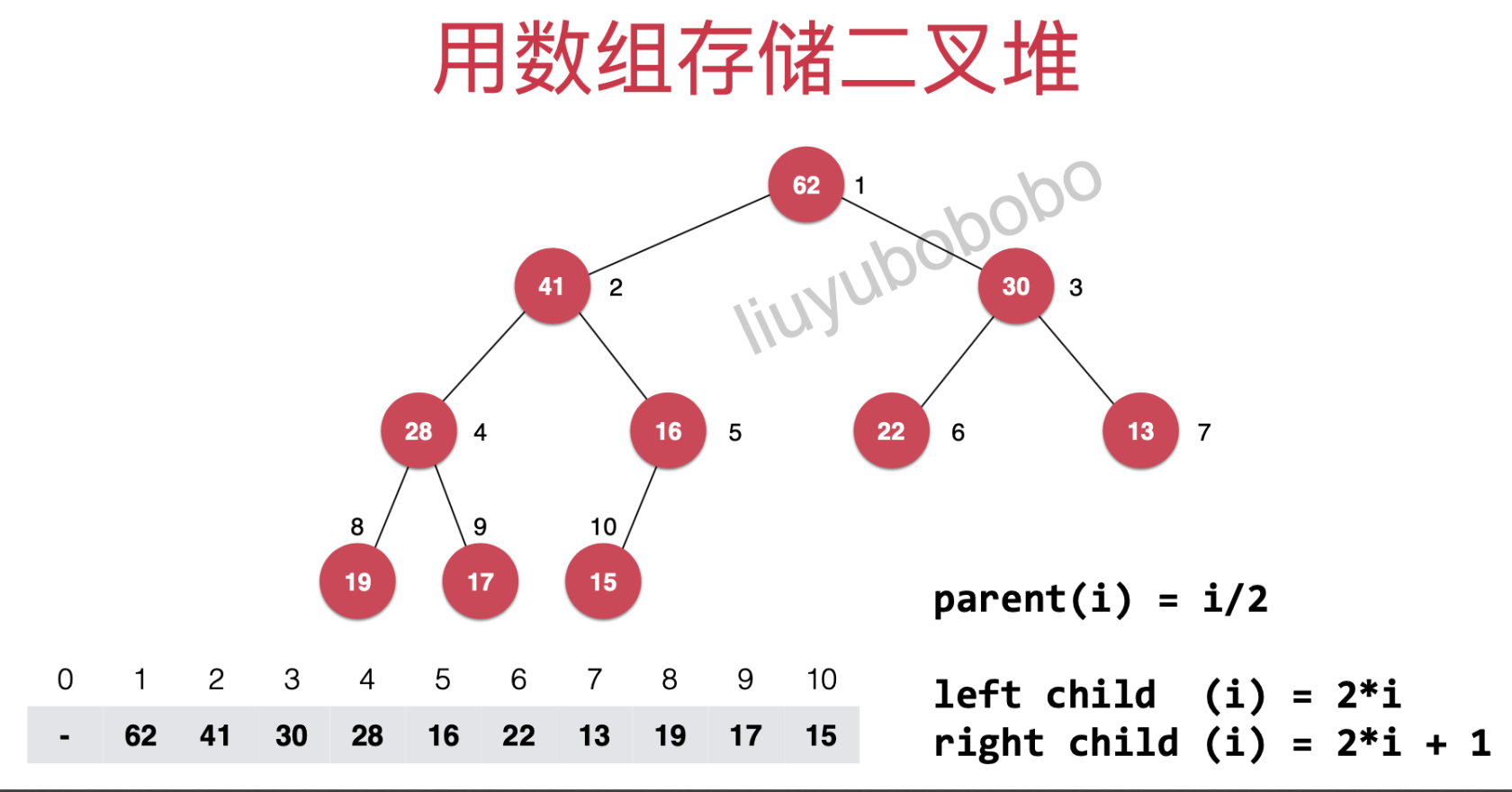
下图用将堆的索引标记出:
三.代码实现(c++)
如何实现堆呢?
第一步:堆的构建
#include <iostream>
#include <algorithm>
#include <string>
#include <ctime>
#include <cmath>
#include <cassert>
using namespace std;
//使用模板函数
template<typename Item>
class MaxHeap{
private:
Item *data; //作为数组的指针
int count; //表示为数组的索引
int capacity; //表示堆的容量
public:
//构造函数
//构造一个空堆
MaxHeap(int capacity) {
//动态的开辟一片空间,并将data指向该空间
data = new Item[capacity + 1];
count = 0;
this->capacity = capacity;
}
//析构函数,将new的空间释放掉
~MaxHeap(){
delete []data;
}
//返回堆的大小
int size(){
return count ;
}
//判断是否为空堆
bool is_empty(){
return count == 0;
}
};现在我们就将堆构造完成了,现在我们构建的堆好像没有什么用,我们还需要对进行数据的插入(Shift Up)和取出(Shift Down)操作,下面分别来实现。
第二步:Shift Up和Shift Down
1. Shift Up
首先我们需要了解什么是Shift Up:
就是将堆中插入元素的操作,其逻辑为:从堆后一个节点插入元素,如下图:


插入元素后必须维护堆的定义,所以需要将新插入的元素做比较,其方法是:
将新元素跟它所在节点的上一个节点 (新元素的父节点) 的数比较,如下图中:
53 > 16 需要将两元素位置互换

互换位置后就变成了下图:
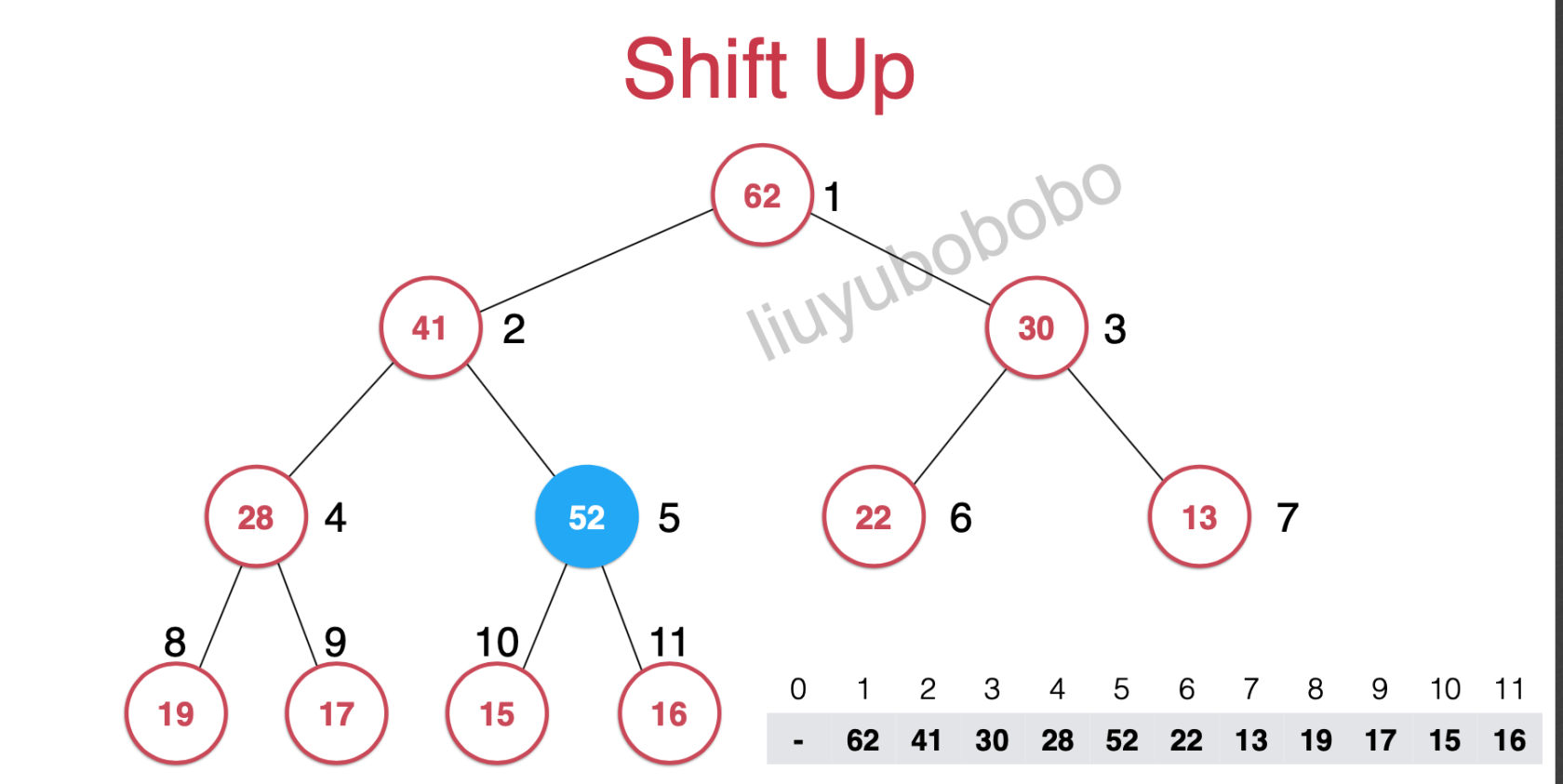
然后仍然需要维护堆的定义所以需要将52和它的父节点的元素做比较:
52 > 41,所以将两元素位置互换
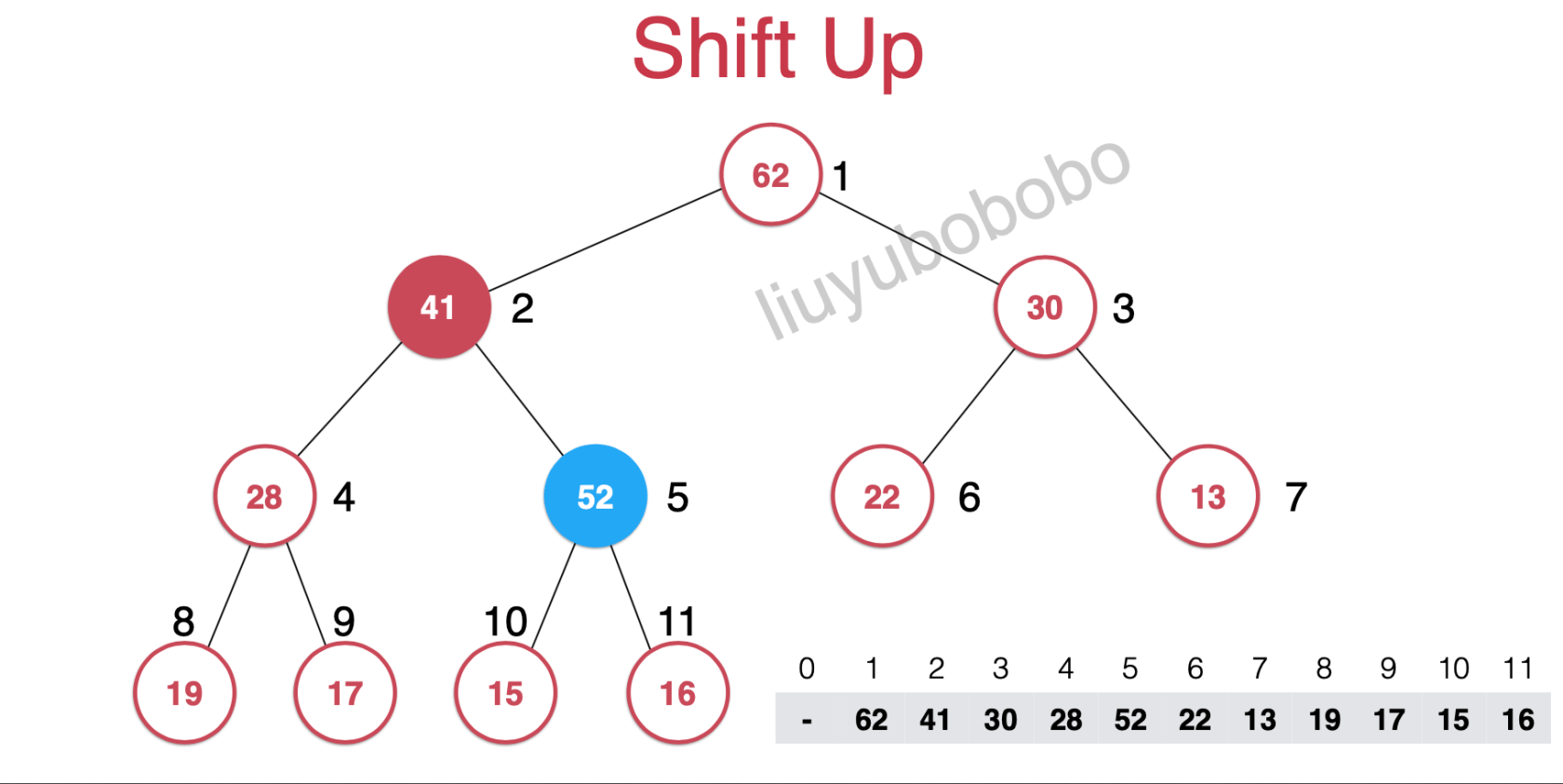
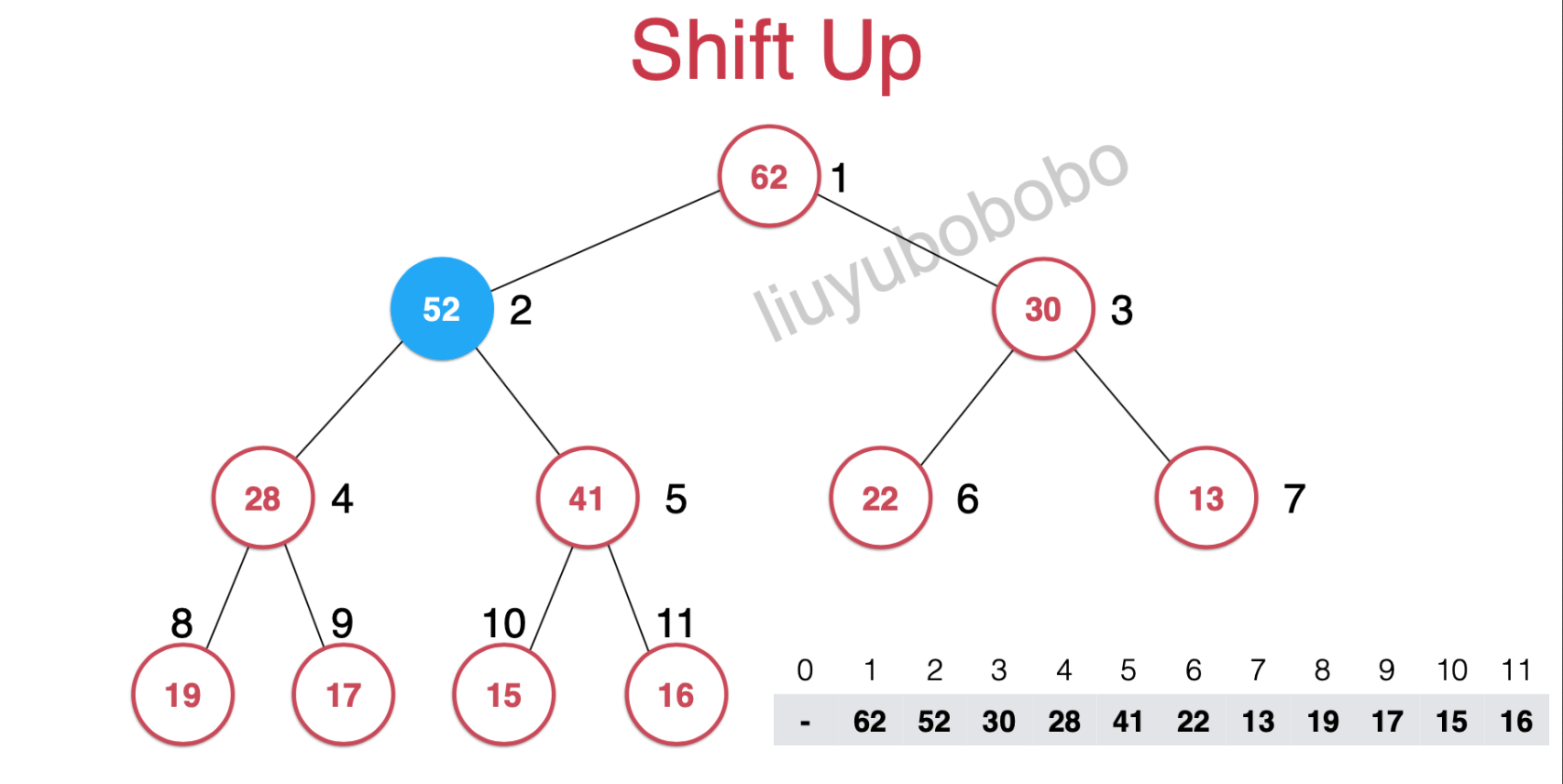
就得到下图,但仍然需要维护堆的定义,所以继续比较
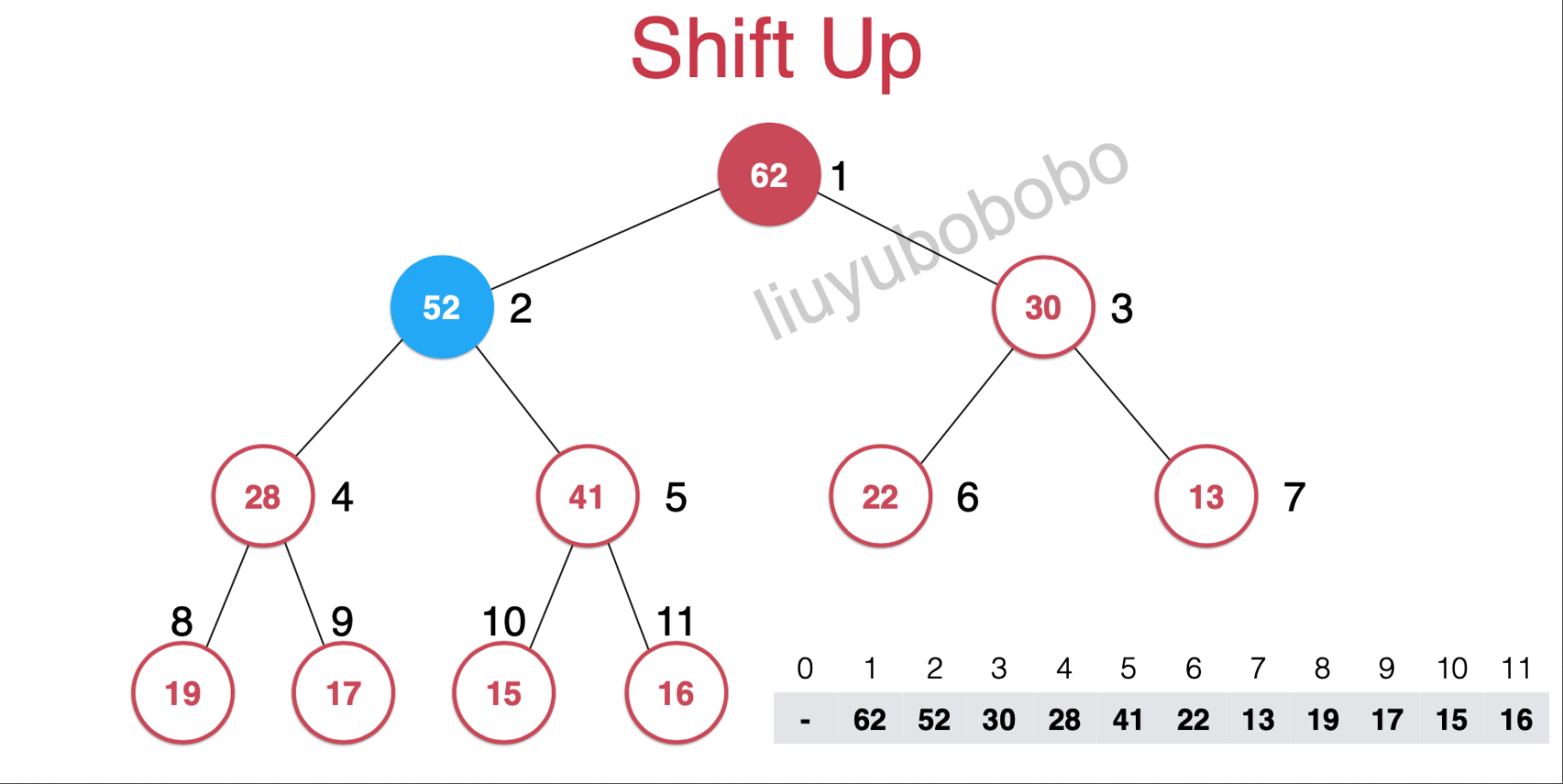
最后就变成了下图
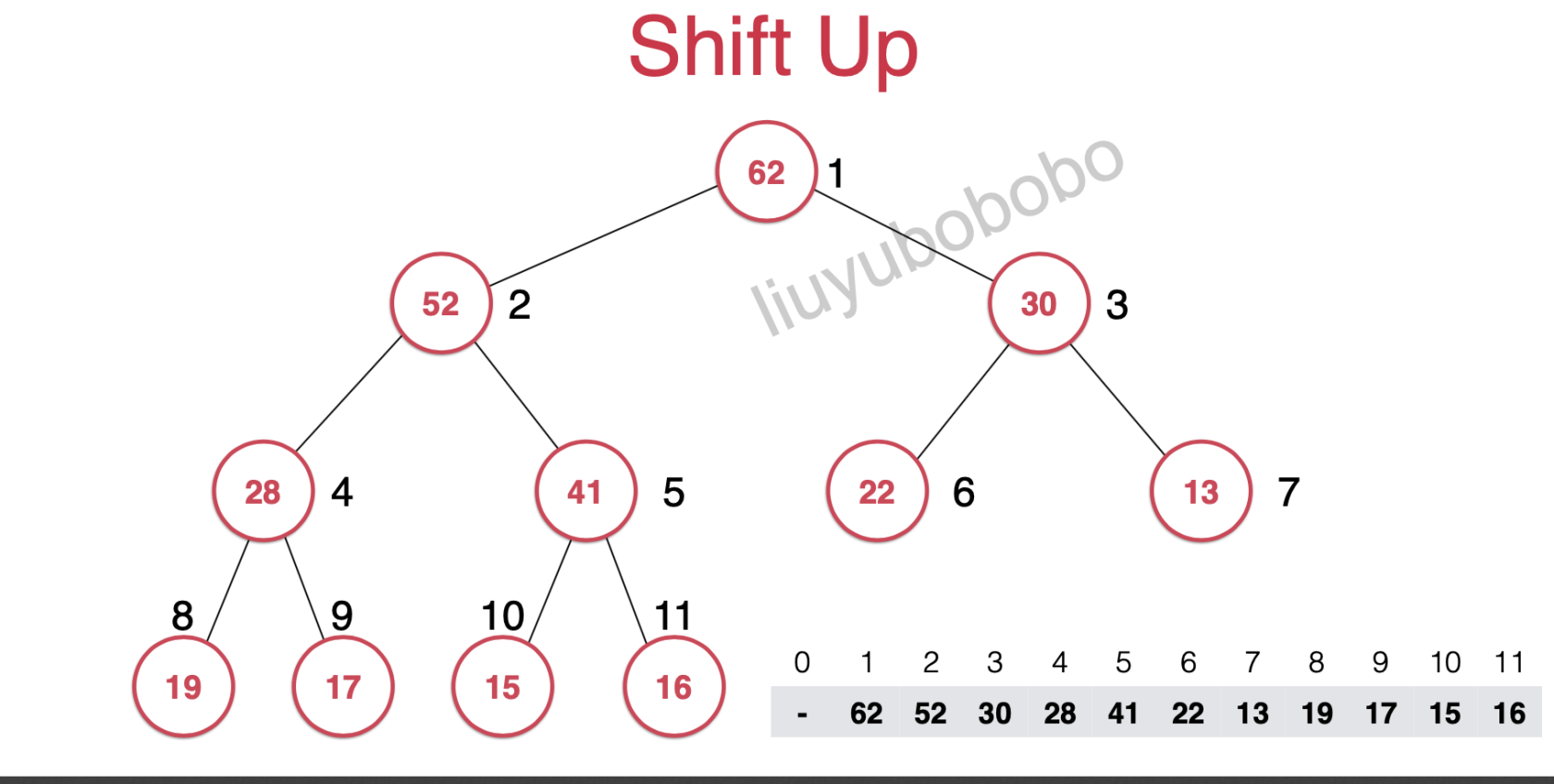
这就是整个ShiftUp操作
下面上代码:
//向堆中插入元素
int insert(Item item){
//我们这里的对的根节点从索引为1开始,所以需要capacity+1的空间
//assert用于判断是否满足capacity+1 > capacity
assert(capacity+1 > capacity);
data[count+1] = item;
count++;
ShiftUp(count);
}这里我将构造函数ShiftUp()写在private中,用户不需要看到我们背后的逻辑
private:
Item *data; //作为数组的指针
int count; //表示为数组的索引
int capacity; //表示堆的容量
//构造shiftUp
void ShiftUp(int k){
while(k>1 && data[k/2] > data[k]){
swap(data[k/2], data[k]);
k/=2;
}
}
完成了Shift Up,下面我们来完成Shift Down
2.Shift Down
Shift Down是指从堆中将元素取出,其取出操作是:

将堆中的第一个元素取出
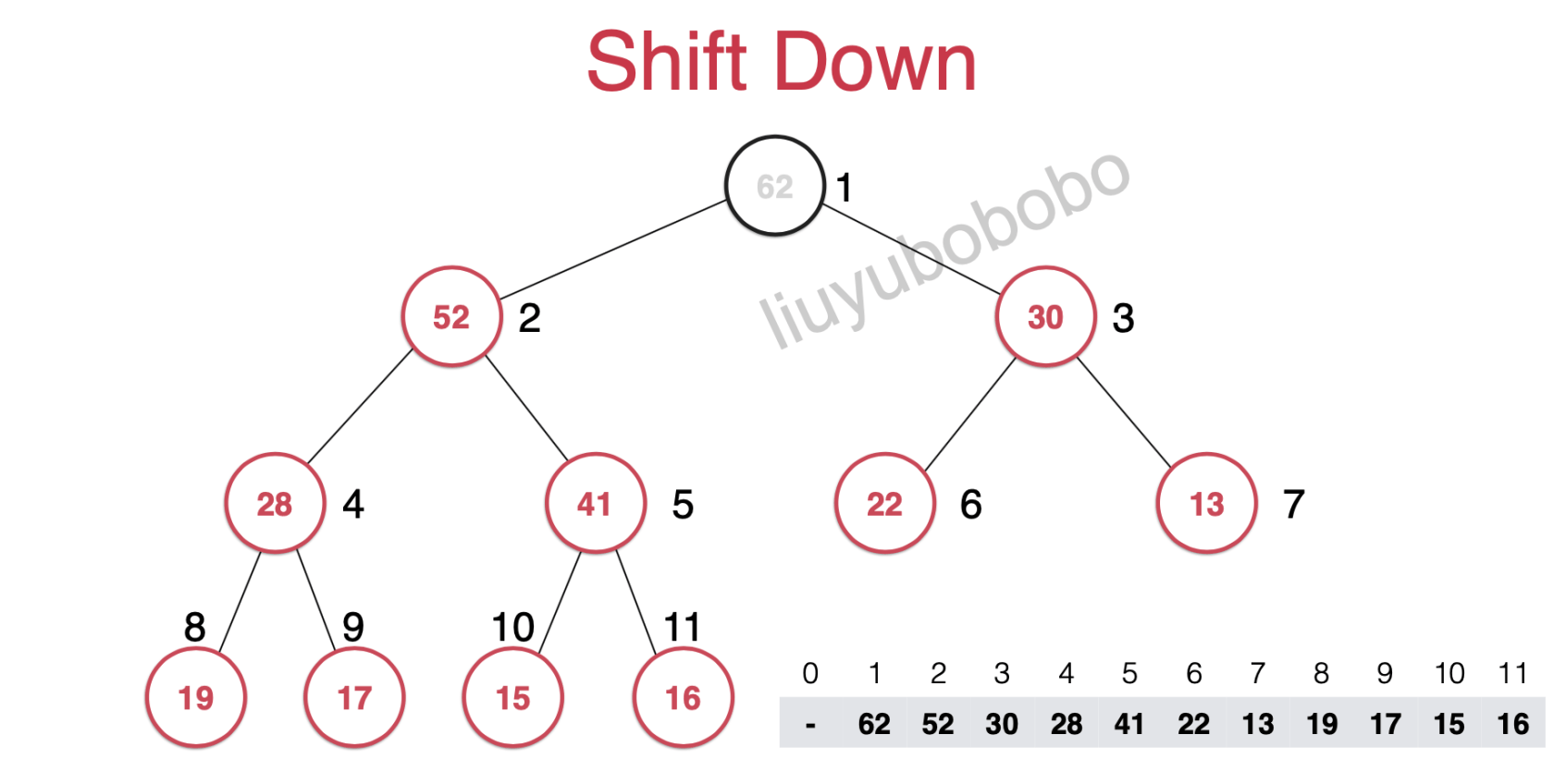
然后将堆最后一个元素放到原来取出元素的位置
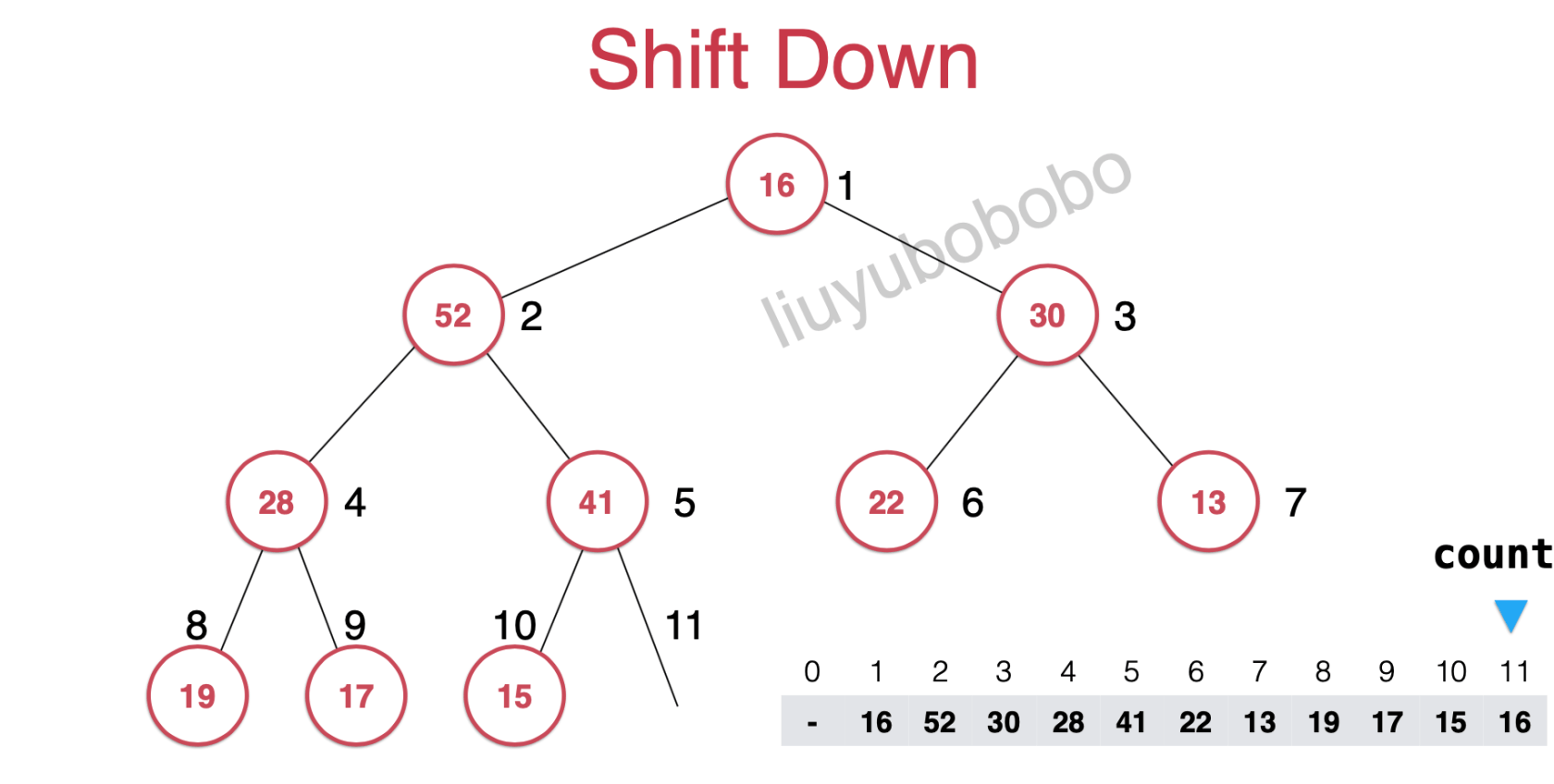
然后将该元素的左右孩子节点的元素进行比较 (如下图将52和30比较),然后将该元素和左右孩子节点中值大的元素进行位置互换
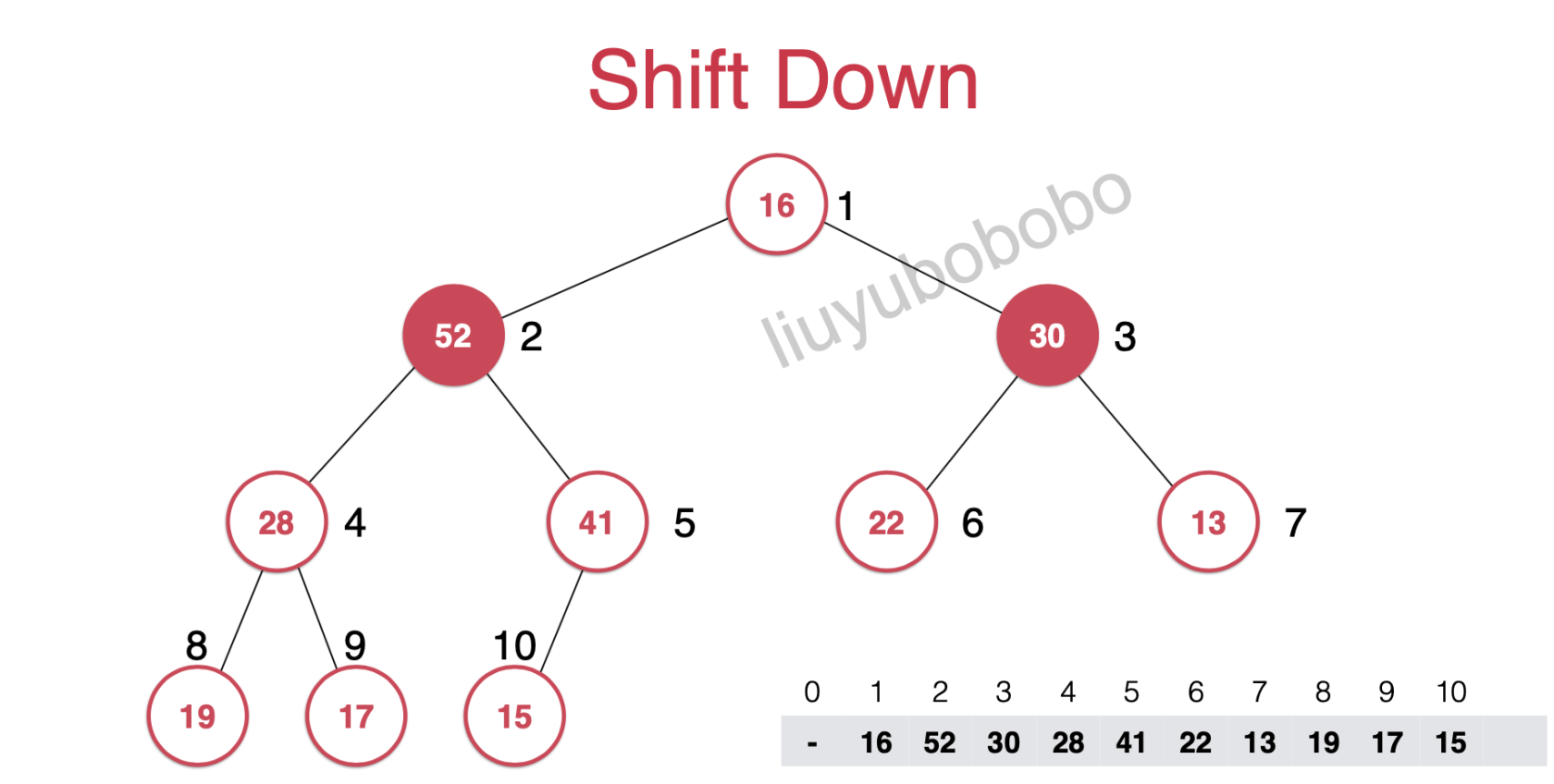
如下图: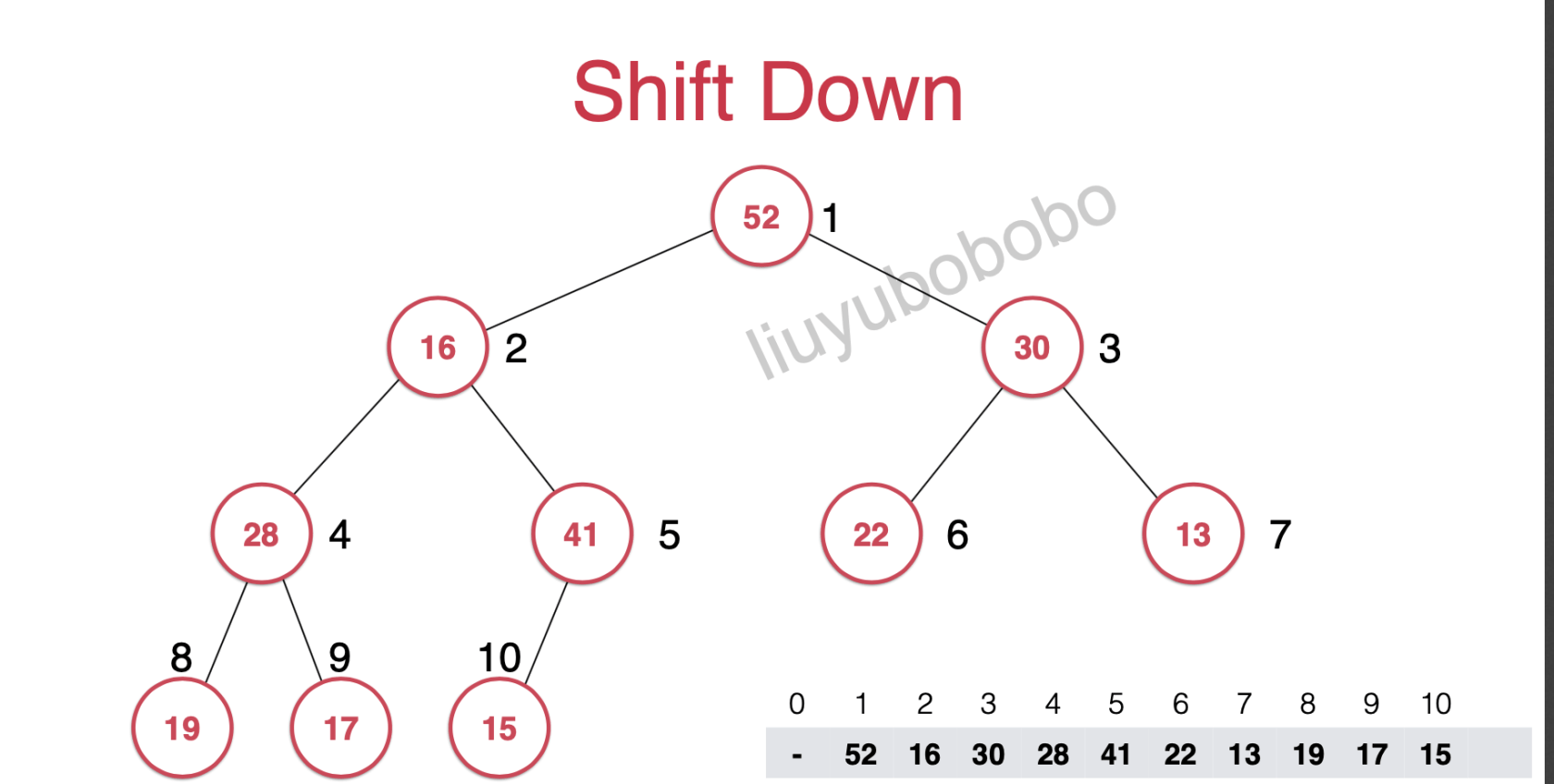
然后在将该元素现在所在的节点的左右孩子节点的元素进行比较
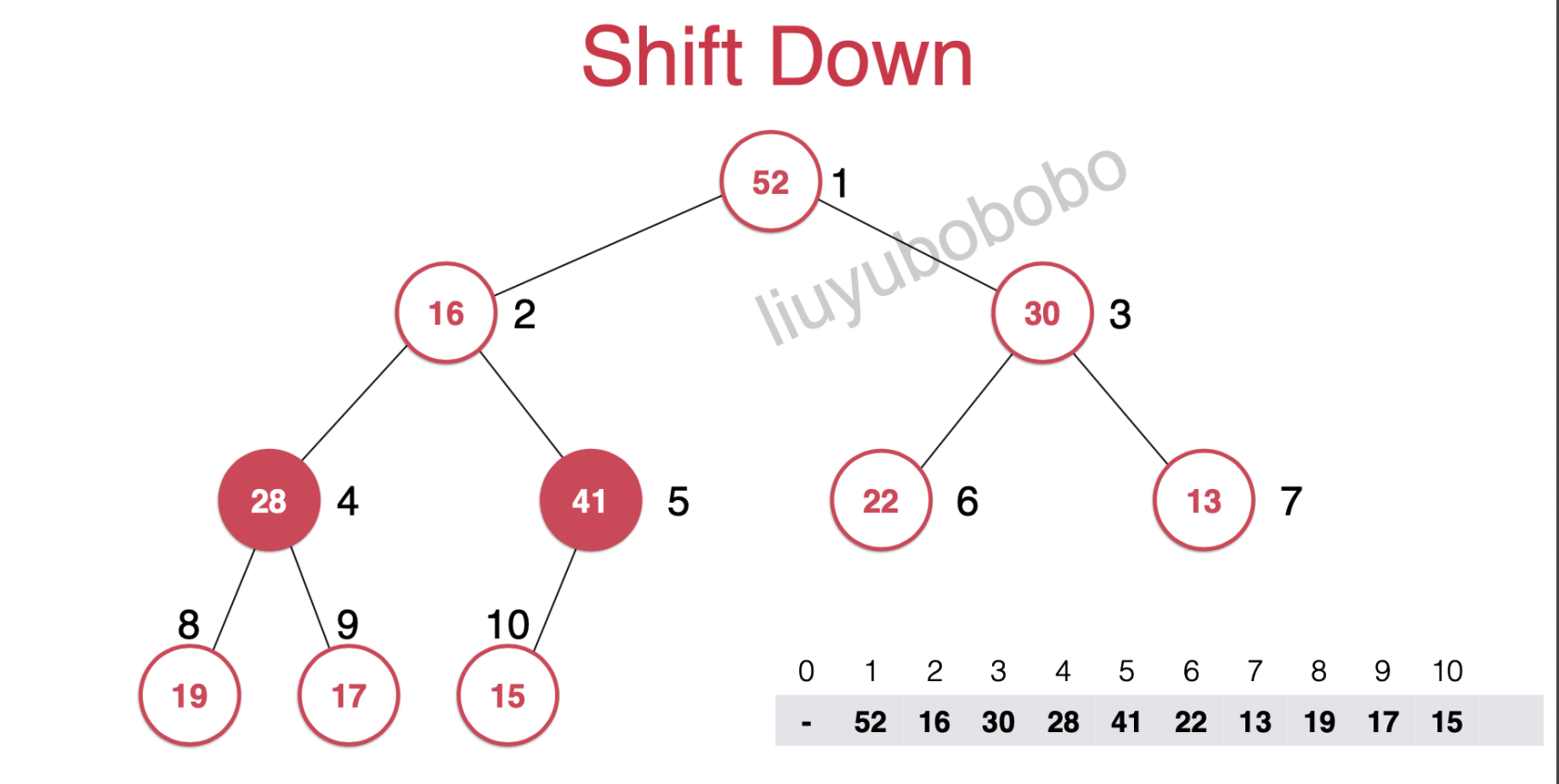
得到如下图: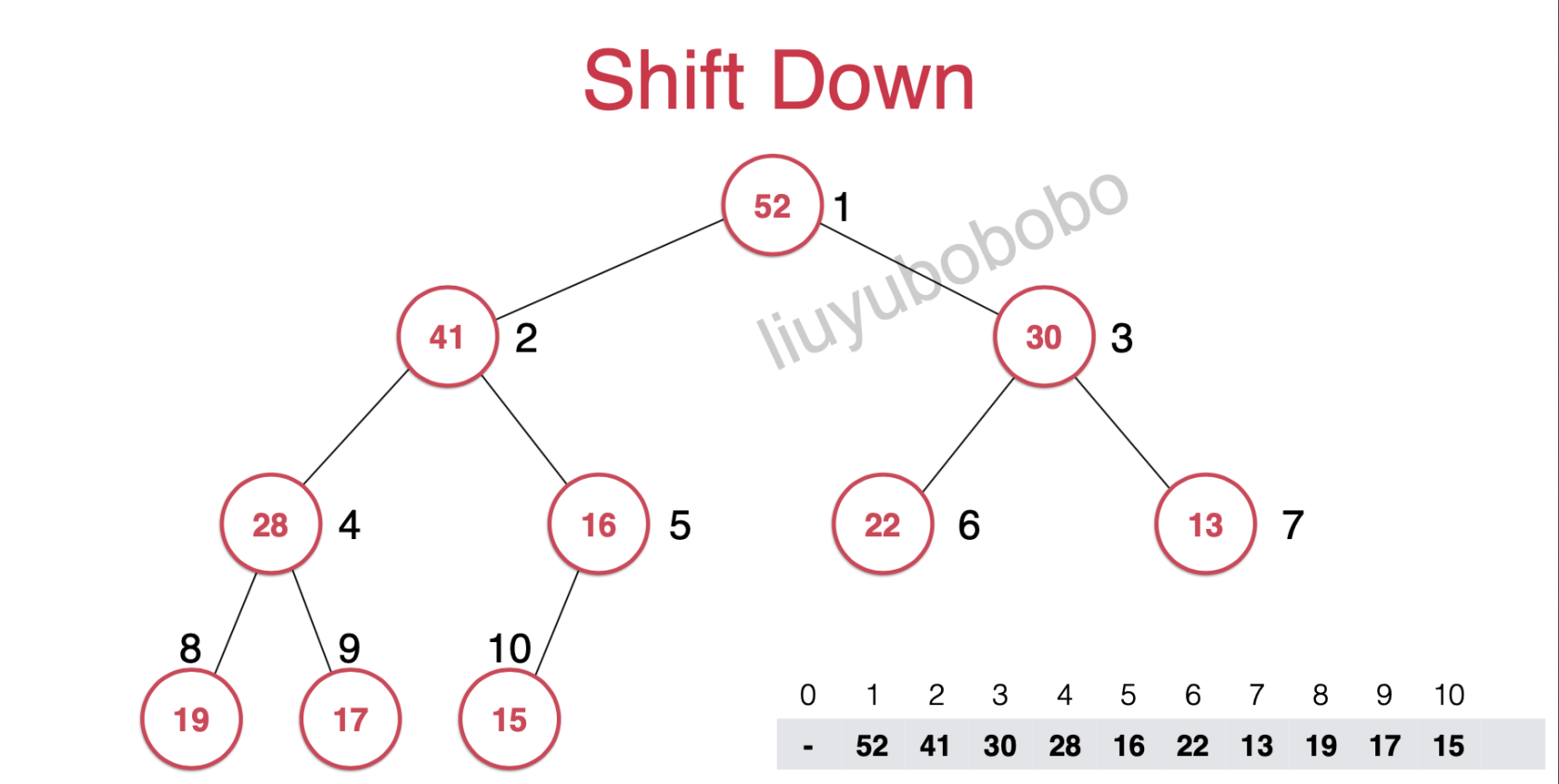
此时还会判断16 和15两元素的大小
此时ShiftDown就完成了
下面上代码:
Item extractMax(){
assert(count>0);
//将第一个元素取出
Item ret = data[1];
//将最后一个元素放置第一个位置
swap(data[1], data[count]);
//将多余的位置消去
count--;
ShiftDown(1);
return ret;
}仍然将ShiftDown放在private中
private:
Item *data; //作为数组的指针
int count; //表示为数组的索引
int capacity; //表示堆的容量
//构造shiftUp
void shiftUp(int k){
while(k>1 && data[k/2] > data[k]){
swap(data[k/2], data[k]);
k/=2;
}
}
void ShiftDown(int k){
//判断是否存在左孩子
while(2*k < count){
int j = 2*k;
//是否存在右孩子
if(j+1 < count && data[j+1] > data[j])
j++;
//data[j]是data[2*k],data[2*k+1]中的最大值
if(data[k] > data[j])
break;
swap(data[k]), data[j];
}
}这样堆就完成了,下面我们将整个源码给出:
#include <iostream>
#include <algorithm>
#include <string>
#include <ctime>
#include <cmath>
#include <cassert>
using namespace std;
//使用模板函数
template<typename Item>
class MaxHeap{
private:
Item *data; //作为数组的指针
int count; //表示为数组的索引
int capacity; //表示堆的容量
//构造shiftUp
void shiftUp(int k){
while(k>1 && data[k/2] > data[k]){
swap(data[k/2], data[k]);
k/=2;
}
}
void ShiftDown(int k){
//判断是否存在左孩子
while(2*k < count){
int j = 2*k;
//是否存在右孩子
if(j+1 < count && data[j+1] > data[j])
j++;
//data[j]是data[2*k],data[2*k+1]中的最大值
if(data[k] > data[j])
break;
swap(data[k]), data[j];
}
}
public:
//构造函数
//构造一个空堆
MaxHeap(int capacity) {
//动态的开辟一片空间,并将data指向该空间
data = new Item[capacity + 1];
count = 0;
this->capacity = capacity;
}
//析构函数,将new的空间释放掉
~MaxHeap(){
delete []data;
}
//返回堆的大小
int size(){
return count ;
}
//判断是否为空堆
bool is_empty(){
return count == 0;
}
int insert(Item item){
//我们这里的对的根节点从索引为1开始,所以需要capacity+1的空间
//assert用于判断是否满足capacity+1 > capacity
assert(capacity+1 > capacity);
data[count+1] = item; //向对插入元素
count++;
shiftUp(count);
}
Item extractMax(){
assert(count>0);
//将第一个元素取出
Item ret = data[1];
swap(data[1], data[count]);
count--;
ShiftDown(1);
return ret;
}
};(图片来源:慕课网bobo老师)
本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu



