二分搜索树系列之「深度优先-层序遍历 (ergodic) 」
二分搜索树的遍历
一.遍历的分类
二分搜索树遍历分为两大类,深度优先遍历和层序遍历。
深度优先遍历分为三种:先序遍历(preorder tree walk)、中序遍历(inorder tree walk)、后序遍历(postorder tree walk),分别为:
1、前序遍历:先访问当前节点,再依次递归访问左右子树。
2、中序遍历:先递归访问左子树,再访问自身,再递归访问右子树。
3、后序遍历:先递归访问左右子树,再访问自身节点。
二. 深度优先遍历
- 前序遍历:先访问当前节点,再依次递归访问左右子树。
- 中序遍历:先递归访问左子树,再访问自身,再递归访问右子树。
- 后序遍历:先递归访问左右子树,再访问自身节点。
为了更好理解深度优先遍历我们使用下图模型:
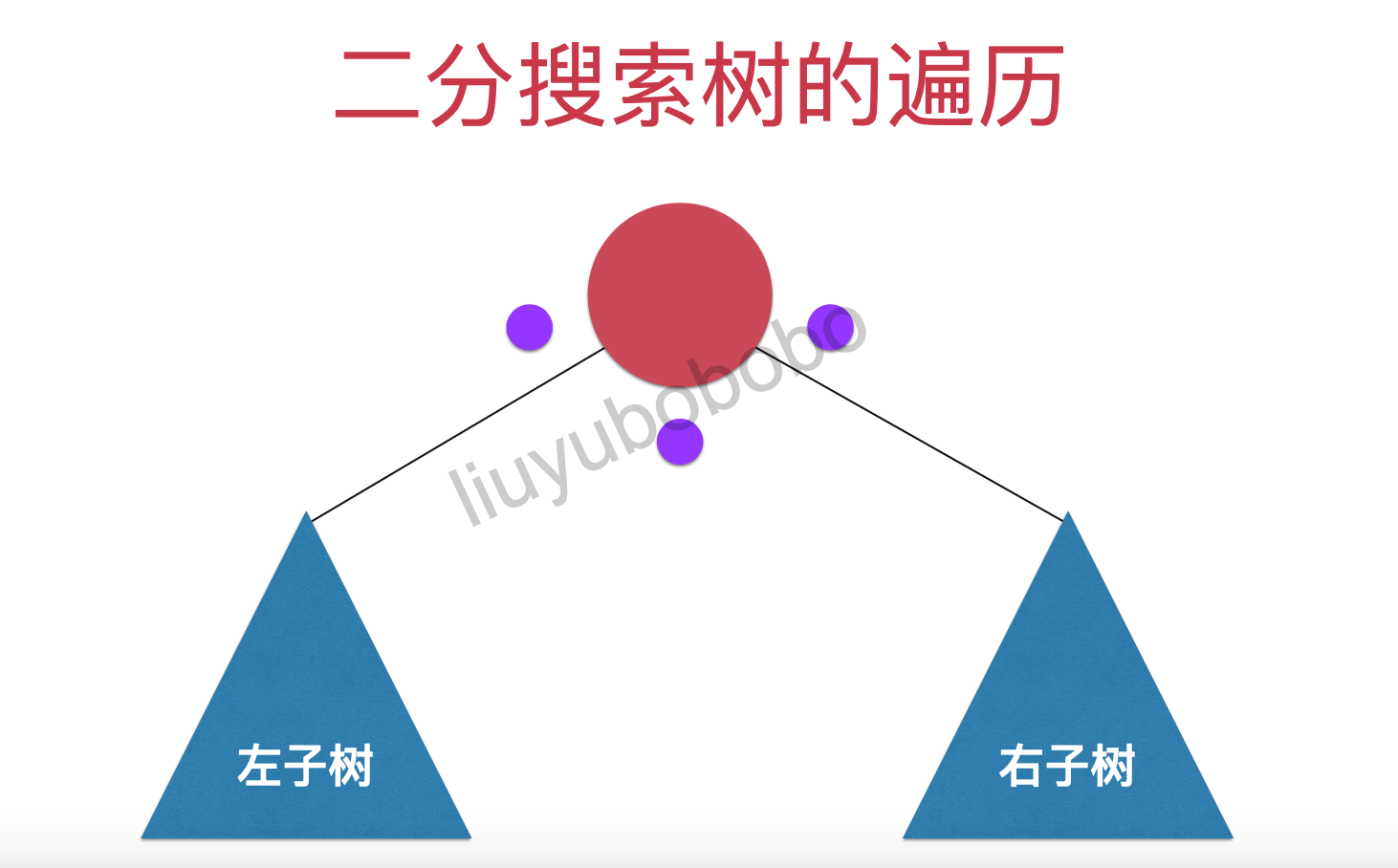
1. 前序遍历:
我们对二分搜索树中所有节点都分别标记3个点:
开始遍历:
前序遍历是对每一个节点第一次访问的时候进行遍历:
28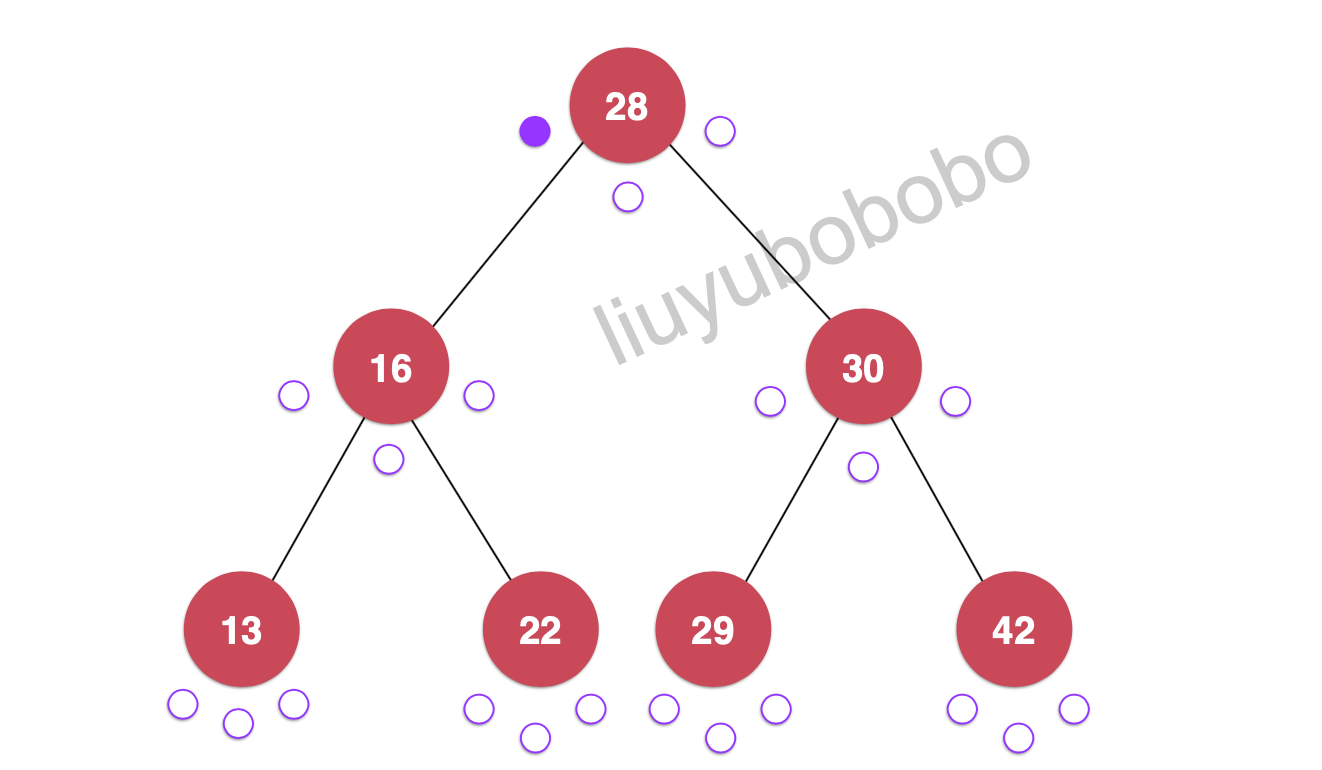
遍历:28, 16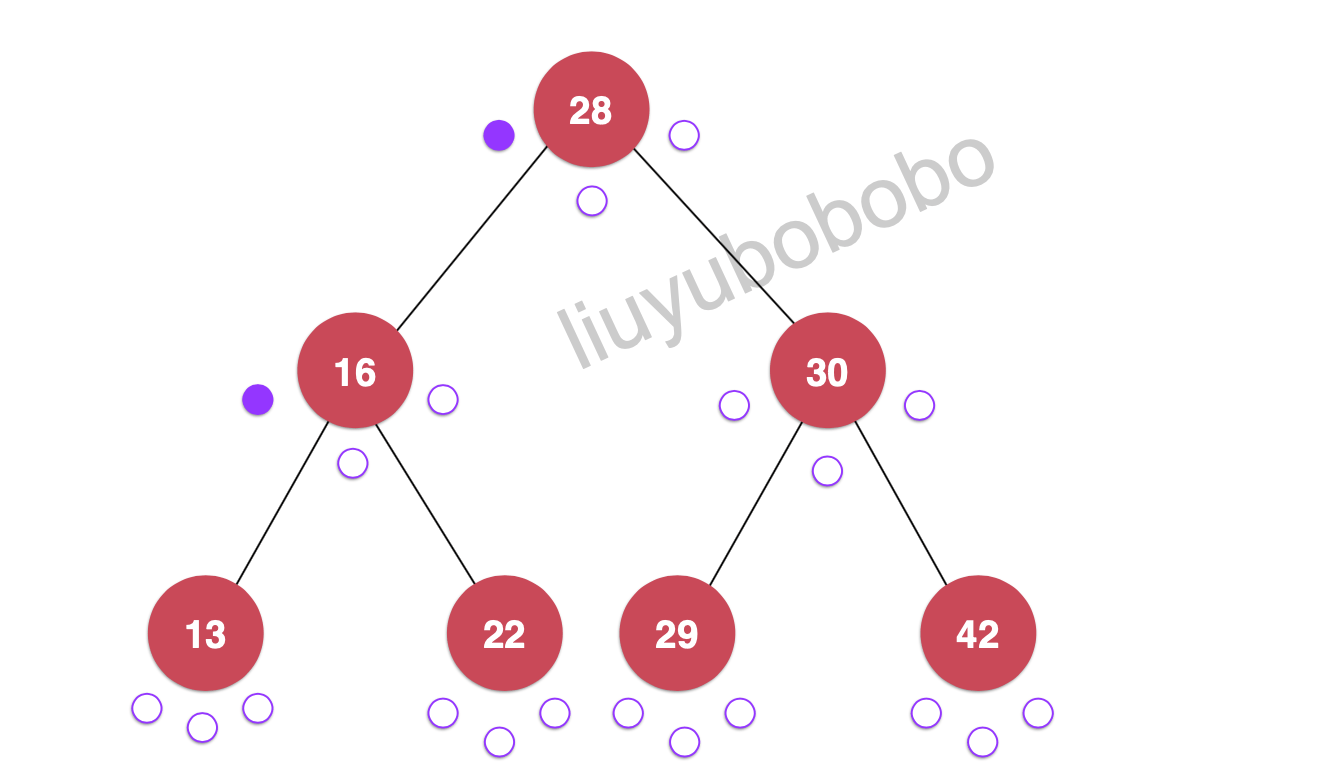
遍历:28, 16, 13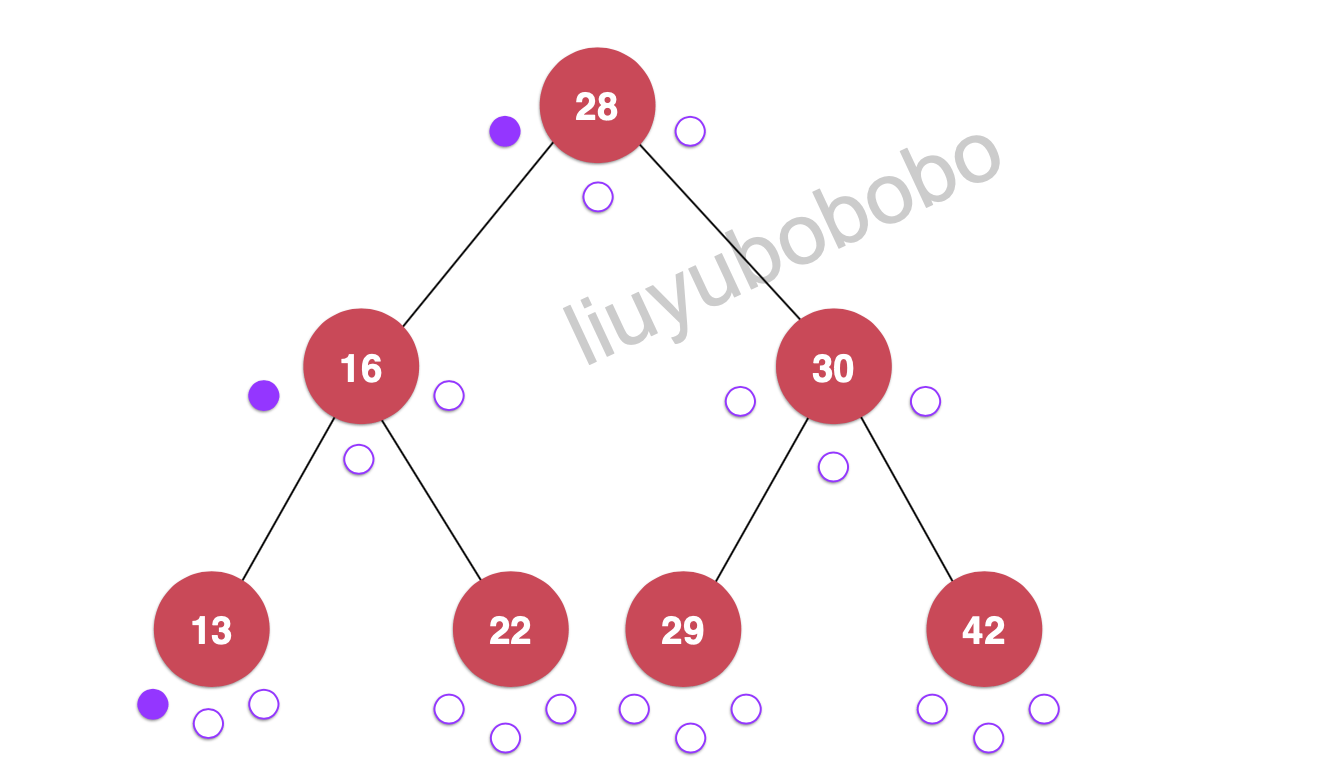
遍历:28, 16, 13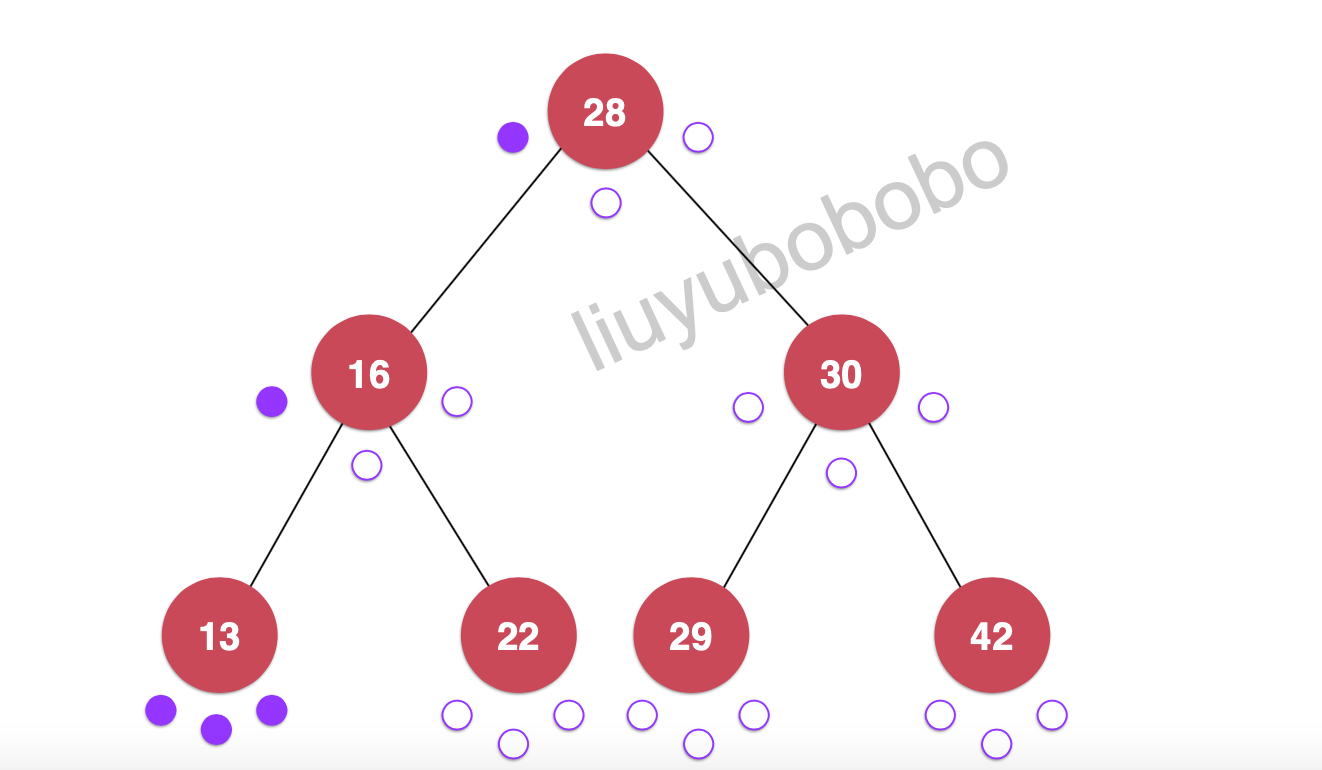
遍历:28, 16, 13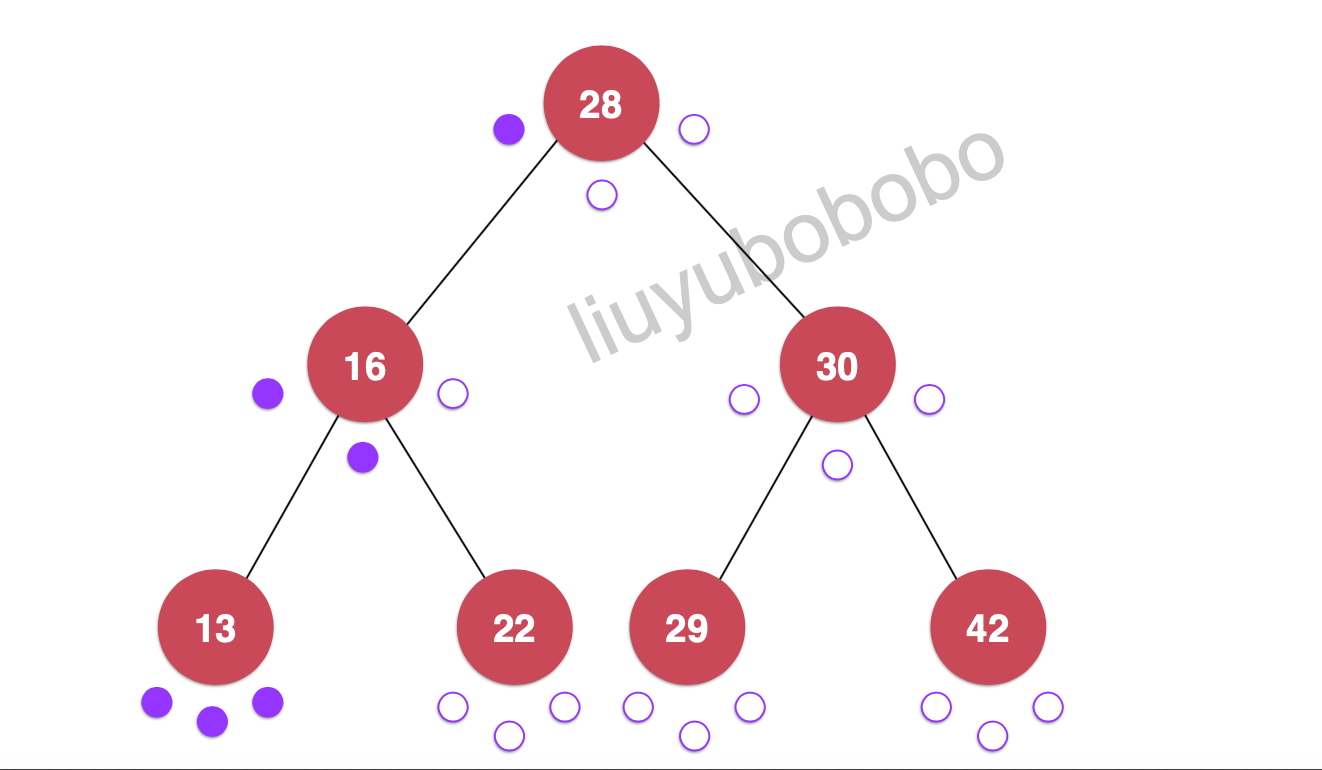
遍历:28, 16, 13, 22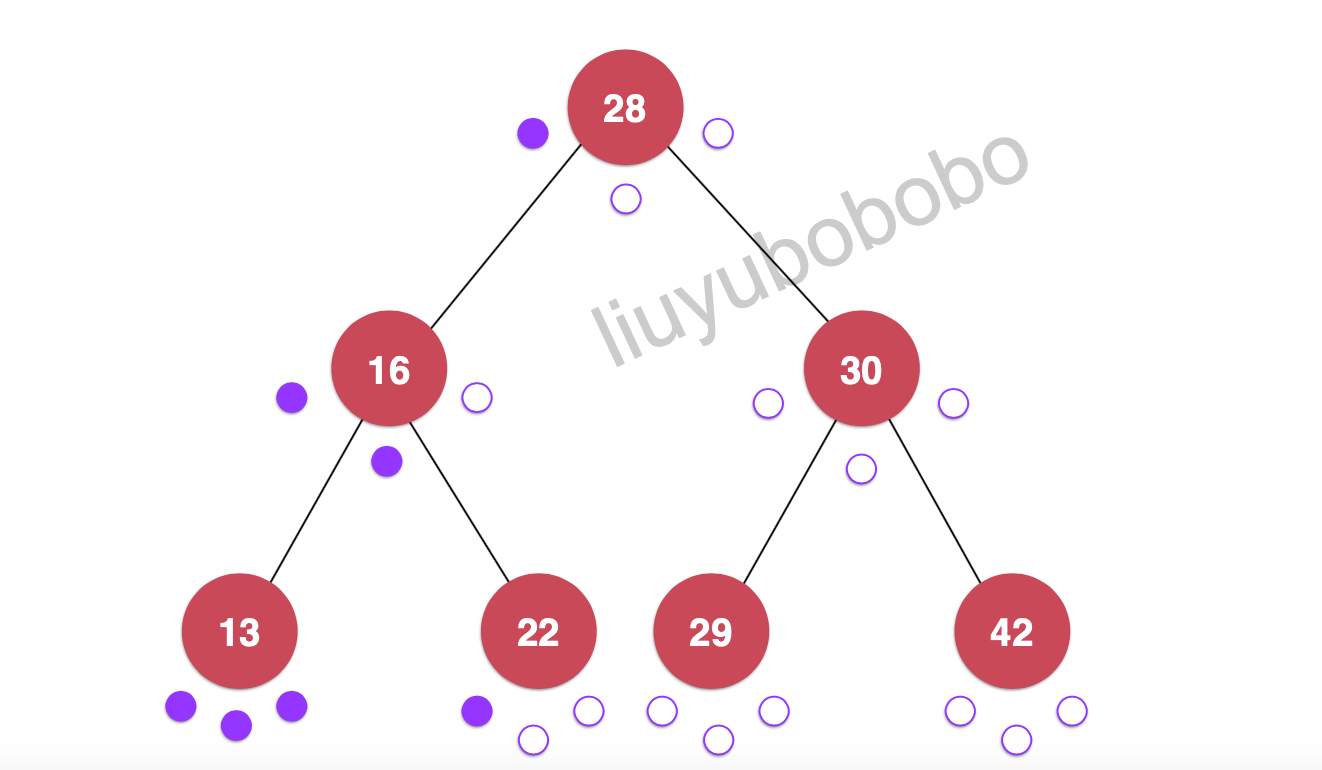
遍历:28, 16, 13, 22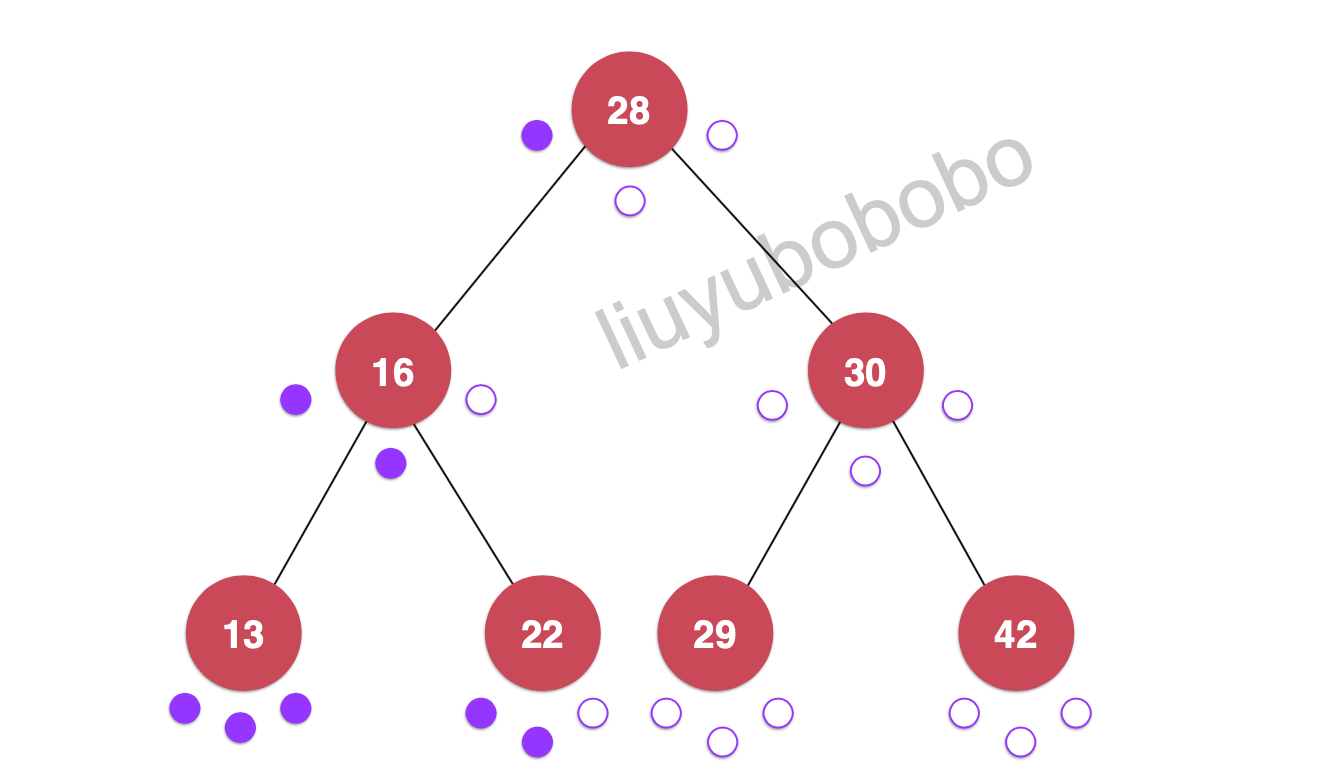
遍历:28, 16, 13, 22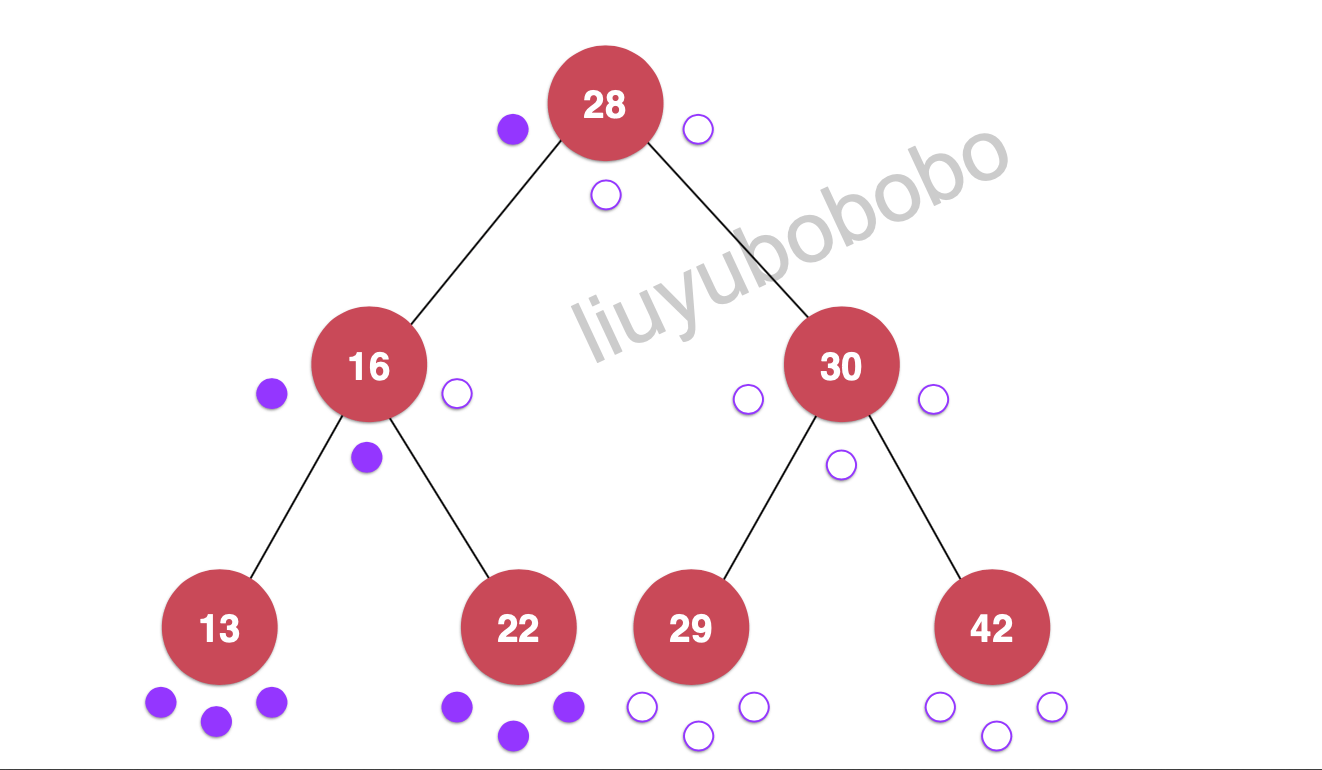
遍历:28, 16, 13, 22
依次类推 ……
最后完成整个前序遍历:
遍历:28, 16, 13, 22, 30, 29, 42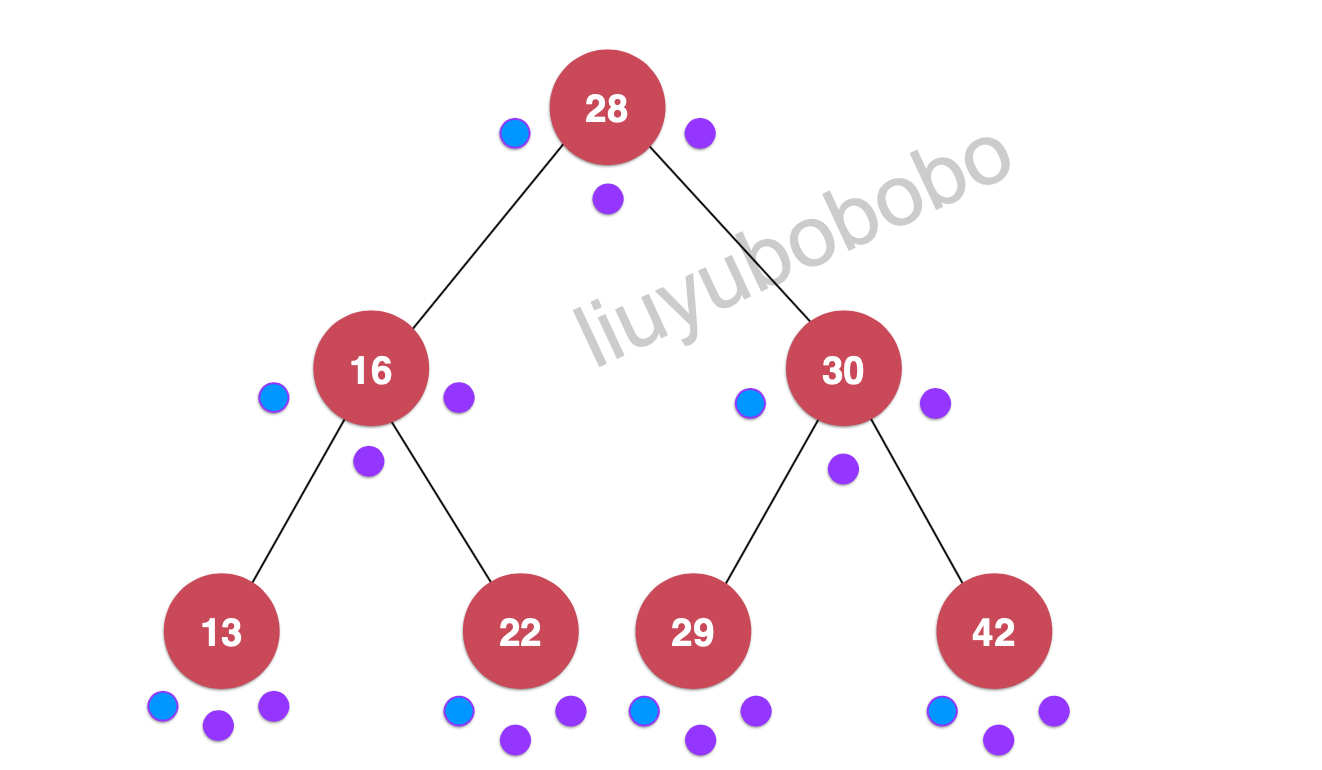
**代码实现(使用递归,c++实现)
在public中定义:
//前序遍历,传入节点,打印节点相应信息
void preOrder() {
return preOrder(root);
}在private中定义:
//前序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void preOrder(Node *node) {
if (node != NULL) {
//不一定用打印,还可以对node->key和node->value进行操作
cout << node->key << endl;
preOrder(node->left);
preOrder(node->right);
}
}2. 中序遍历
按照前序遍历的模型和顺序,很容易看出中序遍历就是在中间点的时候进行遍历:(过程省略)
遍历:13, 16, 22, 28, 29, 30, 42
如下图:(可以看出由中序遍历可以看出遍历结果是有序的)
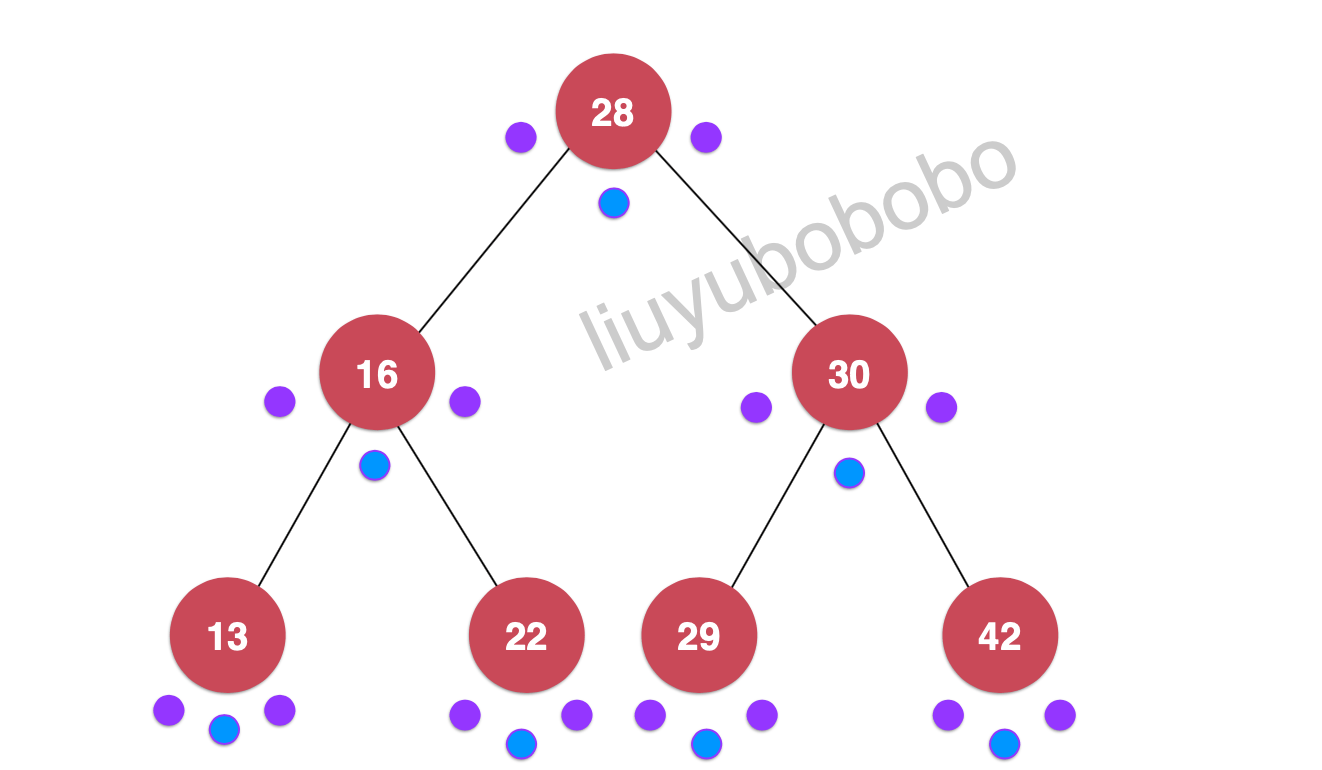
**代码实现(使用递归,c++实现)
在public中定义:
//中序遍历,以节点为node的节点为根节点
void inOrder() {
return inOrder(root);
}在private中定义:
//中序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void inOrder(Node *node) {
if (node != NULL) {
inOrder(node->left);
cout << node->key << endl;
inOrder(node->right);
}
}3. 后序遍历
一样的逻辑,后序遍历就是在第三个点时进行遍历:(过程省略)
遍历:13, 22, 16, 29, 42, 30, 28
如下图: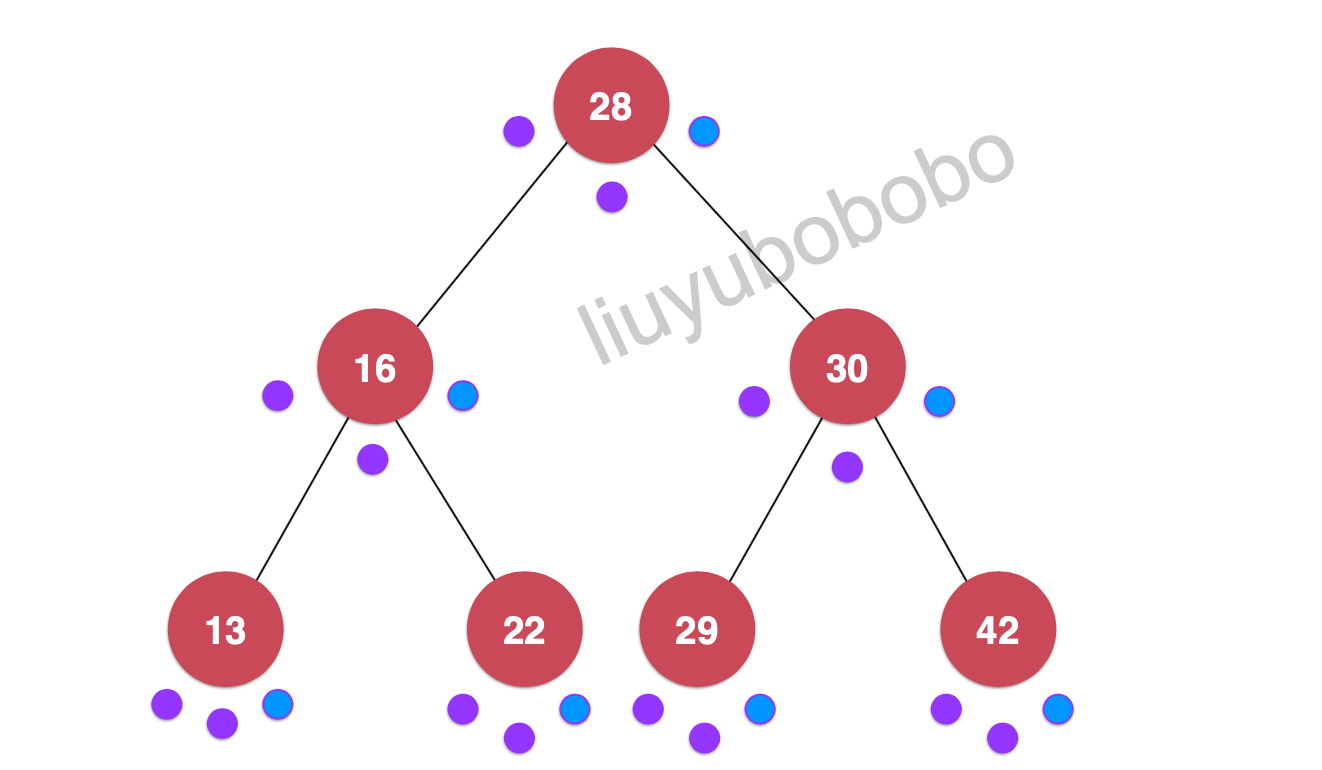
后序遍历有个重要的应用:二叉树的销毁(从子节点依次向上删除)
**代码实现(使用递归,c++实现)
在public中定义:
//后序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void postOrder() {
return postOrder(root);
}在private中定义:
//后序遍历,以node为根节点的二分搜索树进行前序遍历,打印节点相应信息
void postOrder(Node *node) {
if (node != NULL) {
postOrder(node->left);
postOrder(node->right);
cout << node->key << endl;
}
}下面我们来使用后序遍历将二分搜索树销毁:
//析构函数的实现,其本质是后序遍历
void distroy(Node *node) {
if (node != NULL) {
distroy(node->left);
distroy(node->right);
delete node;
count--;
}
}三. 广度优先遍历
1.介绍
二分搜索树的广度优先(层序遍历),即逐层进行遍历,即将每层的节点存在队列当中,然后进行出队(取出节点)和入队(存入下一层的节点)的操作,以此达到遍历的目的。
通过引入一个队列来支撑层序遍历:
如果根节点为空,无可遍历;
如果根节点不为空:
先将根节点入队;
只要队列不为空:
- 出队队首节点,并遍历;
- 如果队首节点有左孩子,将左孩子入队;
- 如果队首节点有右孩子,将右孩子入队;
2.具体数据
以下图为例:![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/ySF0wGBfpa.png!large)
- 我们使用一个队列——front
将28放入队列中
出:空
入:28
队列:28
遍历情况:空![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/JNXew3g72P.png!large)
出:28
入:16, 30
队列:16, 30
遍历情况:28![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/VPQQbBSdWo.png!large)
出:16
入:13 ,22
队列:30, 13, 22
遍历情况:28, 16![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/CgS25HU8lU.png!large)
出:30
入:29 ,42
队列: 13, 22, 29, 42
遍历情况:28, 16, 30![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/xqXqRSEH2L.png!large)
出:13
入:空
队列: 22, 29, 42
遍历情况:28, 16, 30, 13![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/mVMQJoKlrQ.png!large)
出:22
入:空
队列: 29, 42
遍历情况:28, 16, 30, 13, 22![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/b95bmIzhVU.png!large)
出:29
入:空
队列: 42
遍历情况:28, 16, 30, 13, 22, 29![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/xEBErizheX.png!large)
出:42
入:空
队列: 空
遍历情况:28, 16, 30, 13, 22, 29, 42![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/pxWszTUvAk.png!large)
遍历完成:
遍历情况:28, 16, 30, 13, 22, 29, 42![二分搜索树系列之[ 深度优先-层序遍历 (ergodic) ]](https://cdn.learnku.com/uploads/images/202105/20/69310/UleaXFO3nX.png!large)
3.代码实现(使用递归,c++实现)
//层序遍历
void levelOrder(){
queue<Node*> q; //队列d
q.push(root); //将root入队
//队列不为空的情况
while(!q.empty()){
Node *node = q.front(); //将队列第一个元素取出
q.pop(); //是删除栈顶元素
cout<<node->key<<endl;
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
}
本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu



