并查集基于rank的优化

一、介绍

1. 背景
   前面将到并查集基于size的优化，其实仔细想想，还是有可以优化的地方；size[i]是指以i为根节点树的节点数；是将节点数量多的树的根节点向节点数好的树的根节点连接，在一般情况下是得到了优化，但是这里就存在问题了，当出现：节点数多的树它的高度非常高的时候，size的优化方式就不太高效了。
2. rank
   rank[i]:是用来记录以i为根节点的树的高度(树的层数)，其本质是数组。

二、逻辑

并查集本质是树，当树的高度(层数)越高在对数的操作其复杂度会越高，rank的目的就是降低在并(union)过程中并查集的高度；在并(union)过程中使用rank来记录合并的两棵树的高度，将rank值小的树的根节点指向rank值大的根节点。如下图：
连接2，4( union(4,2) )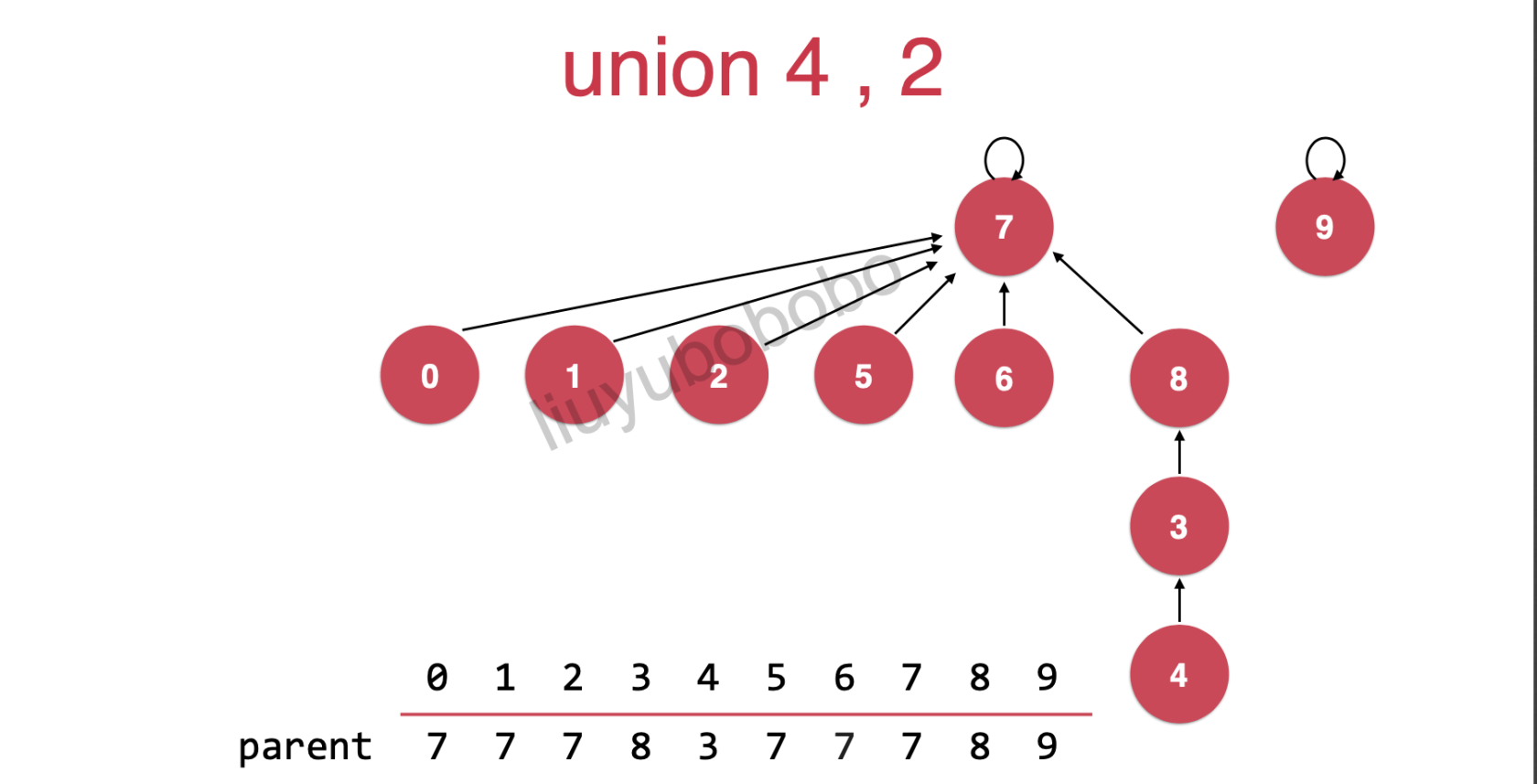

方法一：

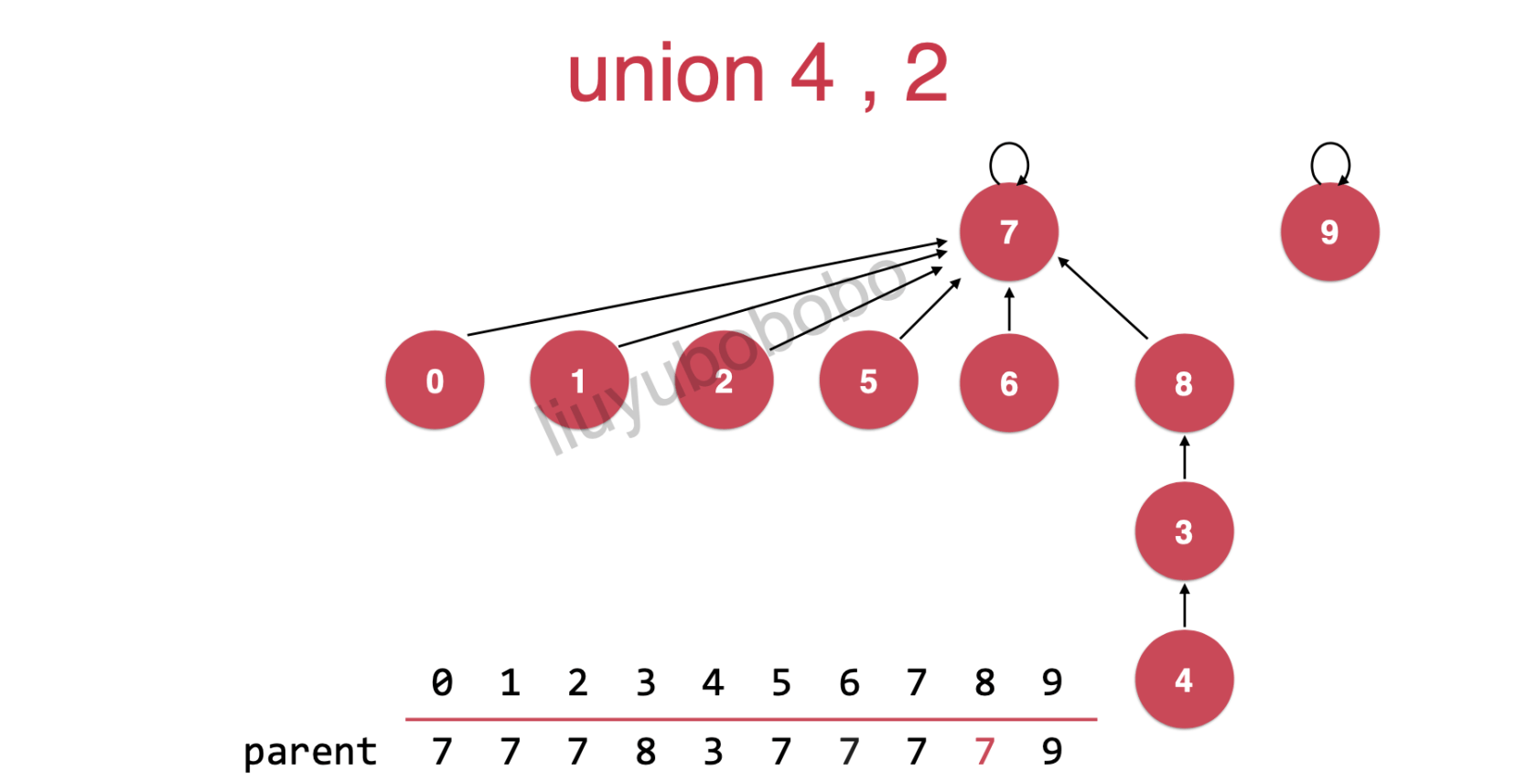
方法二：

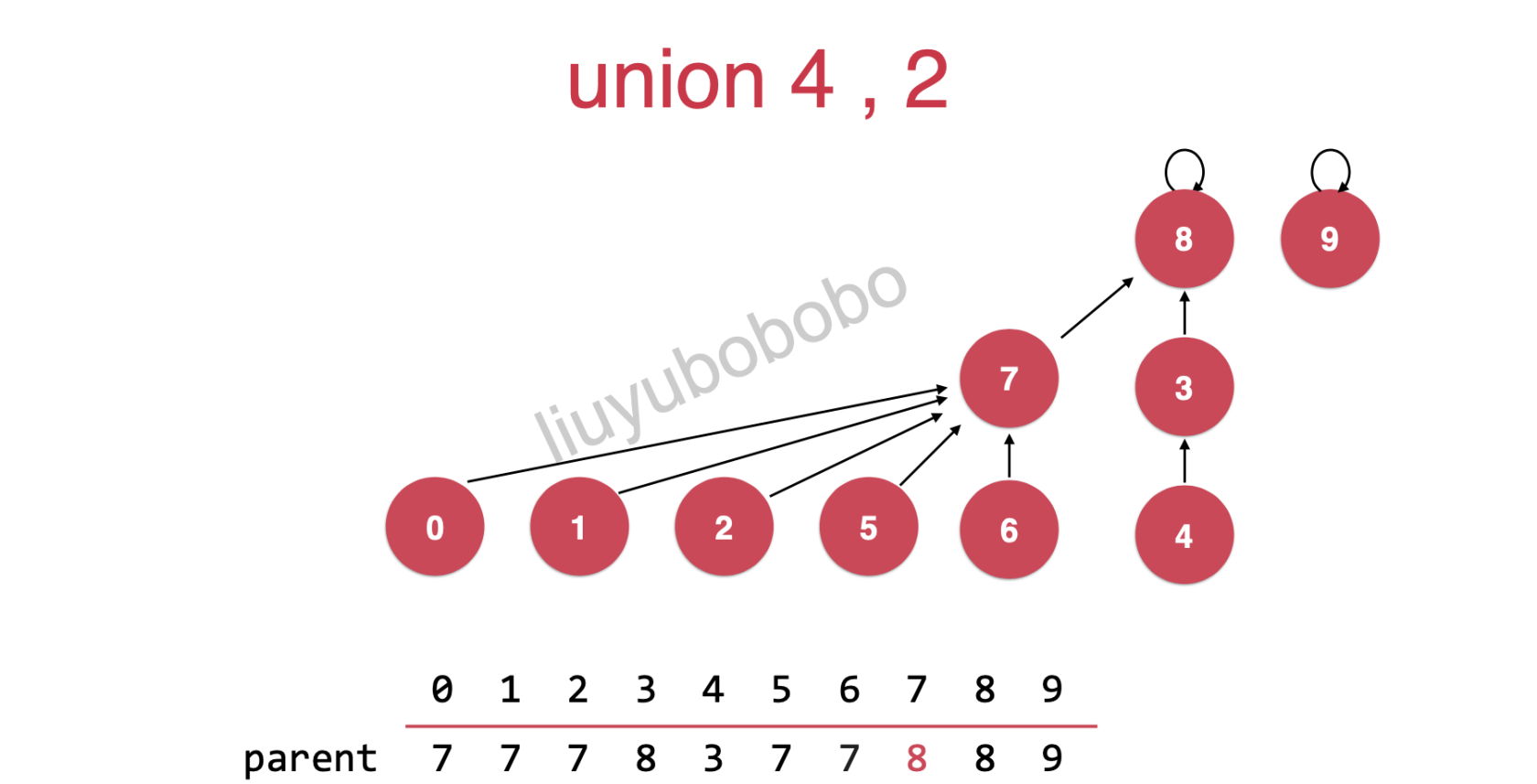
很明显方法二比方法一更优
方法二：正是基于rank的优化
具体逻辑如下：
rank[7] = 2
rank[8] = 3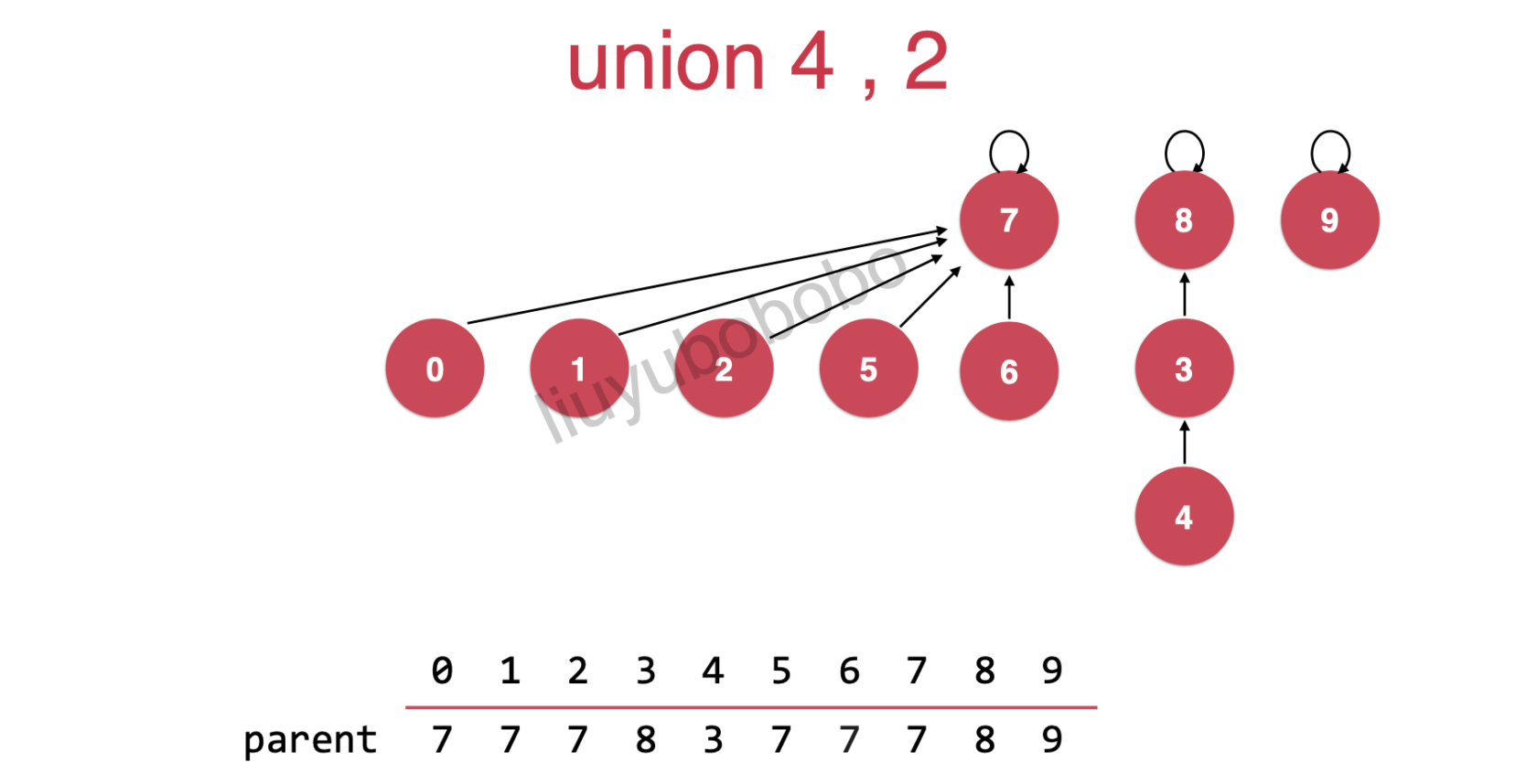

此时只需要将rank[7]树的根节点指向rank[8]树的节点
合并后，如下：
此时整个并查集rank[8] = 3,高度不变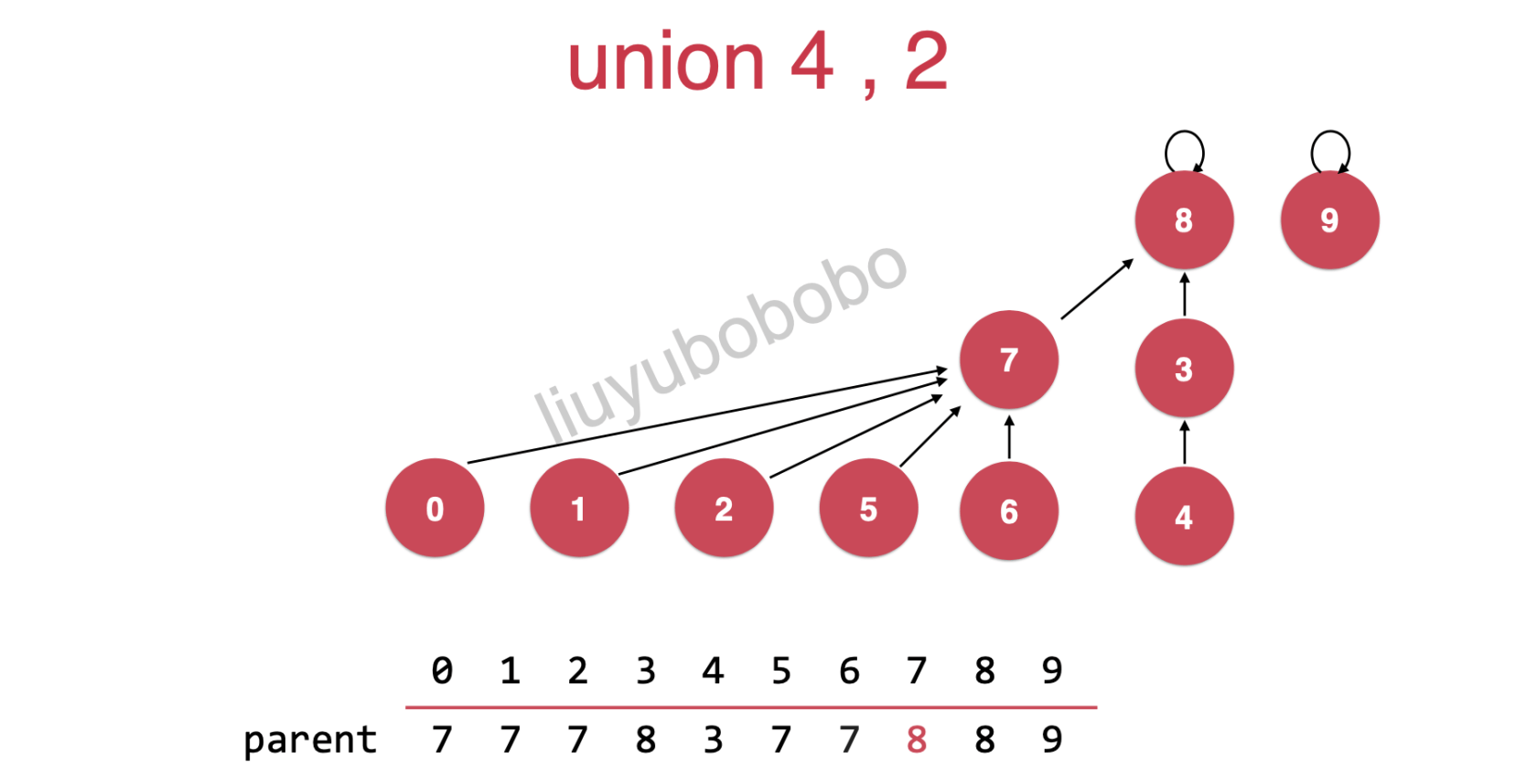

三、代码实现

#include<cassert>

using namespace std;
namespace UF4 {
    class UnionFind4 {
    private:
         // 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
        // parent[i]表示第i个元素所指向的父节点 
        int *parent;
        int *rank;
        int count; //数据个数

     public:
        UnionFind4(int count) {
            parent = new int[count];
            rank = new int[count];
            this->count = count;
            //初始化
            for (int i = 0; i < count; i++) {
                parent[i] = i;
             }
         }
      //析构函数
        ~UnionFind4() {
            delete parent;
            delete rank;
  }

        // 查找过程, 查找元素p所对应的集合编号
 // O(h)复杂度, h为树的高度  
       int find(int p) {
            assert(p >= 0 && p <= count);
  // 不断去查询自己的父亲节点, 直到到达根节点
 // 根节点的特点: parent[p] == p  
        while (p != parent[p])
                p = parent[p];
        return p;
  }

        // 查看元素p和元素q是否所属一个集合
 // O(h)复杂度, h为树的高度 
        bool isConnected(int p, int q) {
            return find(p) == find(q);
  }

rank核心部分:

  // 合并元素p和元素q所属的集合
 // O(h)复杂度, h为树的高度  
      void unionElments(int p, int q) {
              int pRoot = find(p);
              int qRoot = find(q);

              if (pRoot == qRoot)
                   return;
              if (rank[pRoot] > rank[qRoot]) {
                   parent[pRoot] = qRoot;
              } 
              else if (rank[pRoot] < rank[qRoot]) {
                   parent[qRoot] = pRoot;
              } 
              else {//rank[pRoot] == rank[qRoot]
                    parent[qRoot] = pRoot;
                    rank[qRoot] = +1;
              }
        }
    };
}

本作品采用《CC 协议》，转载必须注明作者和本文链接