《剑指offer》之利用单调栈法求直方图最大矩形面积
问题描述
直方图是由排列在同一基线上的相邻柱子组成的图形。
输入是一个由非负数组成的数组,数组中的数字是直方图中柱子的高。
假设直方图中柱子的宽都为 1。
求直方图中最大矩形面积?
例如:输入数组[3,2,5,4,6,1,4,3],其对应的直方图如下图1所示,该直方图中最大矩形面积为12,如阴影部分所示:
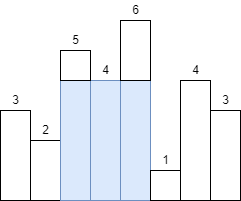
问题分析
矩形的面积等于宽 * 高,因此只要先确定每个矩形的宽和高就能计算出该矩形的面积。
假如直方图中的一个矩形从下标 i 的柱子开始,到下标 j 的柱子结束。
如何确定这个矩形的宽高?
宽:(j - i + 1) * 1;
高:i 到 j 范围内高度最小的柱子的高度为该矩形的高。
例如,图1中从下标为2(i=2)的柱子到下标为4(j=4)的柱子之间的矩形的宽度为 4-2+1=3;高为 4(三根柱子之间最小的高度为 4)。所以面积为 4*3=12。
暴力破解(枚举)
假如能枚举直方图中所有的矩形,并比较它们的面积,便能找到最大的矩形面积。利用两重循环就能实现。代码如下:
<?php
function largestRectangleArea($heights){
$maxArea = 0;
for($i=0;$i<count($heights);$i++){
$min = $heights[$i];
for($j=$i;$j<count($heights);$j++){
// 找到下标从 i 到 j 最小的高度
$min = min($min,$heights[$j]);
$area = $min * ($j - $i + 1);
$maxArea = max($maxArea,$area);
}
}
return $maxArea;
}
$heights = [3,2,5,4,6,1,4,3];
$re = largestRectangleArea($heights);
echo $re; // 输出:12
时间复杂度分析:
如果输入数组的长度为 n,直方图中总共有 O(n2) 个矩形。
计算矩形的面积需要O(1)的时间,那么这种解法的时间复杂度为O(n2)。
进行优化
从左到右的遍历是免不了的。假如以当前柱子的高度为高 hi,当前柱子与其他柱子组成的矩形最大,面积为 maxAreai。依次比较 maxAreai,就可以得到问题的解。
怎么确保以当前柱子的高度为高时,矩形的面积最大?
那么对于每一个柱子,求解它左右的第一个小于它的元素。
什么意思呢?以下标是 3 的柱子为例:该柱子的高度为 4,左边第一个小于 4 的柱子是下标为 2 的柱子,右边第一个小于 4 的柱子是下标为 5 的柱子。当下标为 3 时,最大的矩形如图的阴影部分所示:
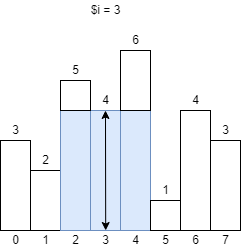
以下是各个柱子所能达到的最大的矩形:
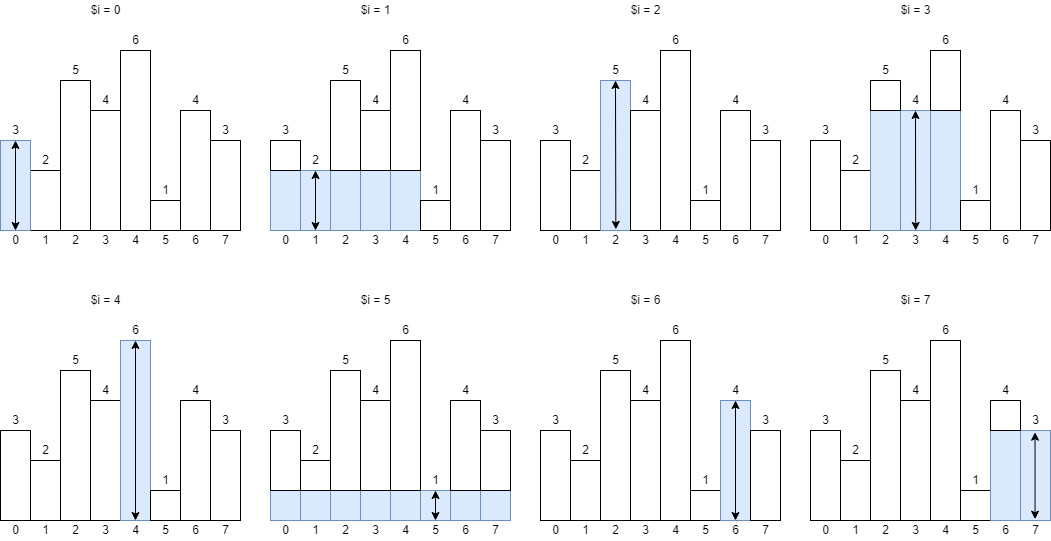
那么对于每一个柱子,该如何求解它左右的第一个小于它的元素呢?这里就用到了单调栈了。
什么是单调栈法
单调栈是一种和单调队列类似的数据结构。
单调队列主要用于 O(n) 解决滑动窗口问题,单调栈则主要用于 O(n) 解决NGE问题(Next Greater Element)。
也就是,对序列中每个元素,找到下一个比它大的元素。(当然,“下一个”可以换成“上一个”,“比它大”也可以换成“比他小”,原理不变。)
在这个例子中,我们要求解每个点左右的第一个小于它的元素,即 NSE 问题(Next Smaller Element)。
这比单调队列还简单一点:
我们维护一个栈,表示“待确定 NSE 的元素”,然后遍历序列。
当我们碰上一个新元素,我们知道,越靠近栈顶的元素离新元素位置越近。所以不断比较新元素与栈顶,如果新元素比栈顶小,则可断定新元素就是栈顶的 NSE,于是弹出栈顶并继续比较。
直到新元素不比栈顶小,再将新元素压入栈。显然,这样形成的栈是单调递增的。
单调栈法的具体实现
1. 完整代码:
<?php
function largestRectangleArea($heights){
$stack = [-1];
$count = count($heights);
$maxArea = 0;
for($i=0;$i<$count;$i++){
// 栈顶元素不等于 -1 并且当前柱子的高度比下标为栈顶的柱子的高度小则出栈。
while(array_peek($stack) != -1 && $heights[$i] <= $heights[array_peek($stack)]){
$height = $heights[array_pop($stack)];
$width = $i - array_peek($stack) - 1;
$maxArea = max($maxArea,$height * $width);
}
// 直到当前柱子的高度不比下标为栈顶的柱子的高度小,再将当前柱子的下标压入栈。
array_push($stack,$i);
}
while(array_peek($stack) != -1){
$height = $heights[array_pop($stack)];
// 矩形的宽度。
// 栈中存储的是柱子的下标。如果当前柱子的高度小于栈顶柱子的高度,那么矩形的宽度就为当前柱子的下标减去栈顶柱子的下标再减1。
$width = $count - array_peek($stack) -1;
$maxArea = max($maxArea,$height *$width);
}
return $maxArea;
}
// 辅助函数,用于获取栈顶的元素,换句话说是获取数组的最后一个元素。
function array_peek(array $arr){
return $arr[count($arr)-1];
}
$heights = [3,2,5,4,6,1,4,3];
$re = largestRectangleArea($heights);
echo $re; // 输出:12
2. 模拟一下示例的过程:
初始输入:
$heights = [3,2,5,4,6,1,4,3];
$stack = [-1]; -1 可以理解为整个直方图最左边的一个高度为0,下标为 -1的柱子。如图:
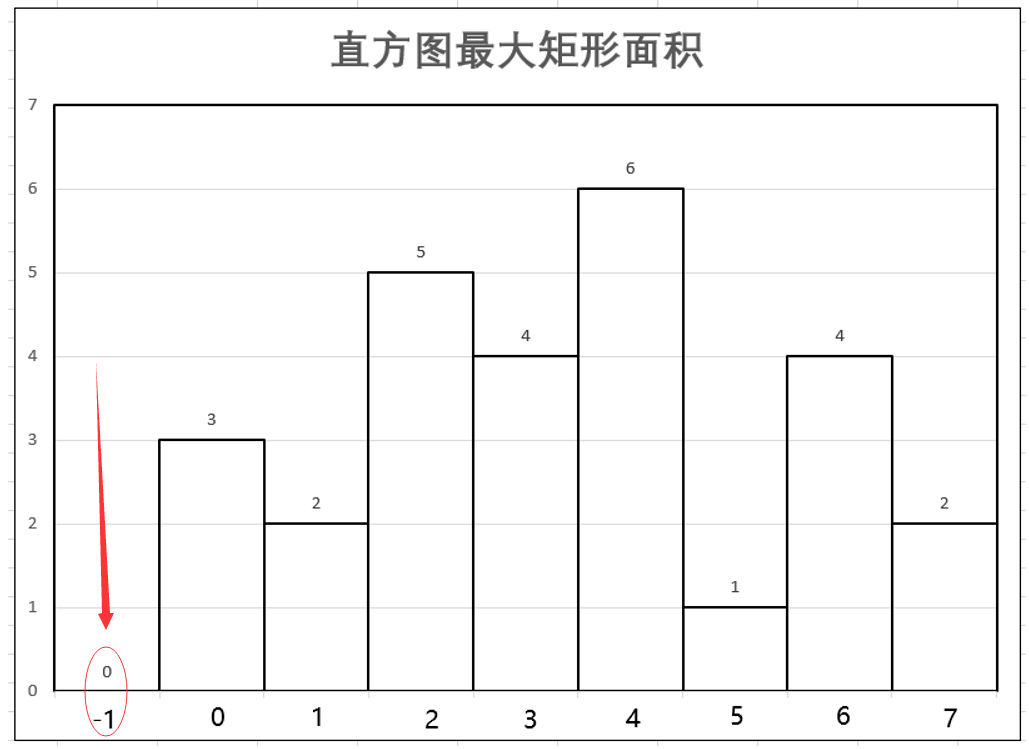
说明:
$stackPeek = array_peek($stack);(栈顶,数组的最后一个元素)
| $i | $hights[$i] | $stackPeek | $heights[$stackPeek] | 动作 | $stack |
|---|---|---|---|---|---|
| 0 | 3 | -1 | 不存在 | $i=0入栈 | [-1,0] |
| 1 | 2 | 0 | 3 | 0出栈 | [-1] |
| 1 | 2 | -1 | 不存在 | $i=1入栈 | [-1,1] |
| 2 | 5 | 1 | 2 | $i=2入栈 | [-1,1,2] |
| 3 | 4 | 2 | 5 | 2出栈 | [-1,1] |
| 3 | 4 | 1 | 2 | $i=3入栈 | [-1,1,3] |
| 4 | 6 | 3 | 5 | $i=4入栈 | [-1,1,3,4] |
| 5 | 1 | 4 | 6 | 4出栈 | [-1,1,3] |
| 5 | 1 | 3 | 4 | 3出栈 | [-1,1] |
| 5 | 1 | 1 | 2 | 1出栈 | [-1] |
| 5 | 1 | -1 | 不存在 | $i=5入栈 | [-1,5] |
| 6 | 4 | 5 | 1 | $i=6入栈 | [-1,5,6] |
| 7 | 3 | 6 | 4 | 6出栈 | [-1,5] |
| 7 | 3 | 5 | 1 | $i=7入栈 | [-1,5,7] |
遍历完数组之后,栈中还剩下一些“待确定NSE的元素”,不过已经没有比这些元素更矮的柱子了,所以只需要依次出栈即可,直到栈顶的值为 -1。
| $stack | $stackPeek | 等于-1? | 动作 |
|---|---|---|---|
| [-1,5,7] | 7 | 否 | 7出栈 |
| [-1,5] | 5 | 否 | 5出栈 |
| [-1] | -1 | 是 | 结束 |
出栈意味着已经具备了处理该柱子的条件。
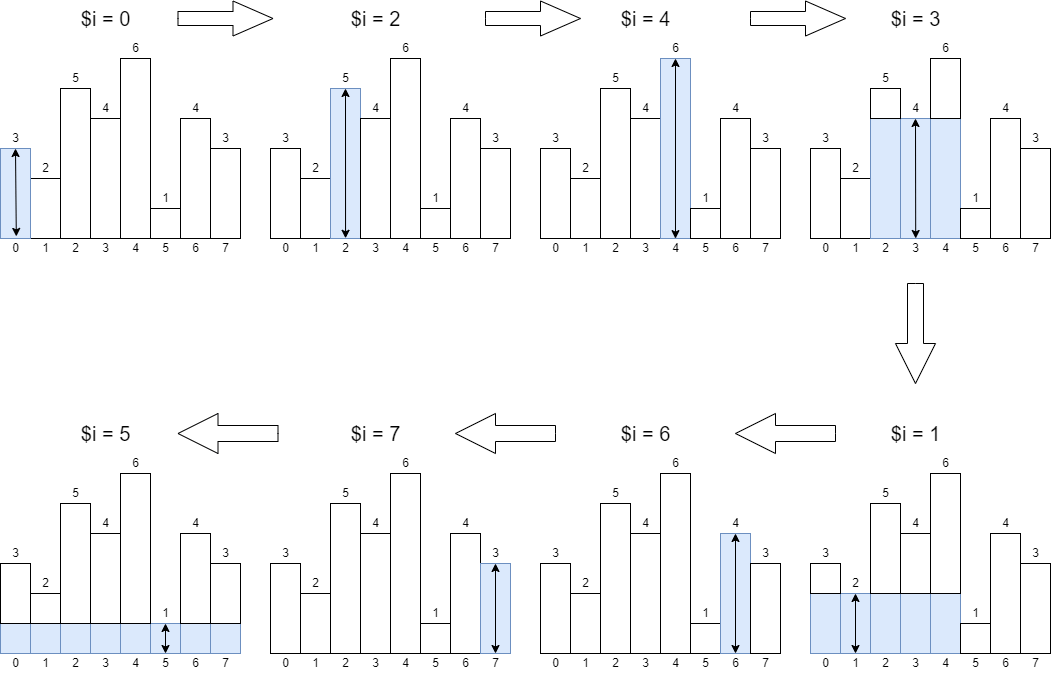
出栈的顺序:0 -> 2 -> 4 -> 3 -> 1 -> 6 -> 7 -> 5 。如图:
时间复杂度
假设输入数组的长度为 n。直方图的每根柱子都入栈、出栈一次,并且在每根柱子的下标出栈时计算以它为顶的最大面积,这些操作对每根柱子而言时间复杂度是O(1),因此这种单调栈法的时间复杂度是O(n)。
总结
这里得到的一个通用思路就是:
利用单调栈的特性,可以在线性时间内求得每一个点它的左右第一个比它大/小的点。
类似问题
1. 矩阵中的最大矩形问题。
2. 每日温度。
3. the next greater number 问题。
参考资料
1. 《剑指offer》
本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu



