杂谈:为何mysql使用B+树作为索引
为何使用B+Tree作为数据库索引
最近在看一些面试题准备找工作 看到了这些准备自己总结分享一下,仅供分享参考 有问题可以交流改进
首先贴一个各种数据结构的一个演示网站USF Data Structure Visualizations
各位可以自己去玩玩
而后会讲讲各类数据结构部分的特性再到b+ tree吧
为何不用哈希(Hash Table)
首先第一个问题 为何不用hash(当然存在哈希索引)?
因为范围查找不方便以及存在hash碰撞
比如有以下数组[1,14,5,6,7,28,21,40] 我们设计一个简单的hash函数如 n % 13
那么便会存在以下情况(第一行为key)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 28 | 5 | 6 | 7 | 21 | ||||
| 14 | |||||||||
| 40 |
当我们在找21时那非常的简单 21% 13 = 8 找key为8就好,而查找40时则会返回一串 1,14,40而后需要遍历对比查找才能找到40,这便是所谓的hash碰撞,并且也不适用于范围查找比如查找返回大于20的值。
但hash的查找速度理论上是最快的为 O(1)
为何不使用二叉搜索(排序)树(BTS)
首先理解二叉搜索树的概念具体可以看 BTS wiki
提炼一下就是
若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
任意节点的左、右子树也分别为二叉查找树;
上图
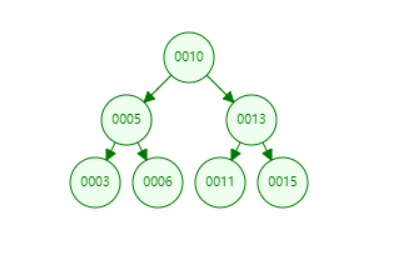
如图 比如需要查找 6 那么顺序便会是 10 -> 5 -> 6 具体便是
6 与 10比较 6 < 10那么向左节点查找
6与 5比较 6 > 10 那么向右节点查找
6与 6比较 查找到了返回
那么这个树有什么问题吗,有 如果我插入 1, 2,3,4,5,6那么就会成为
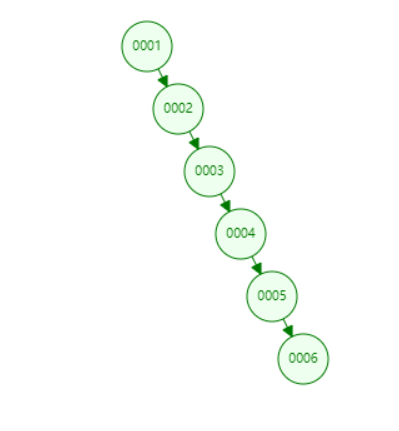
那么如果我现在要查6 就需要6步
那么最坏的时间复杂度则是O(n) n代表树的高度
为何不使用自平衡二叉搜索树
AVL树(Adelson-Velsky and Landis Tree)
先上概念AVL树wiki
重点在于,在AVL树中,任一节点对应的两棵子树的最大高度差为1
很简单便是 如果你插入 1,2,3
就会从这样
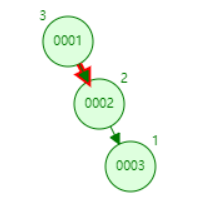
而后1左旋成
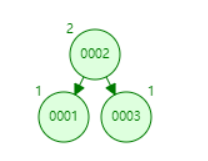
这样(绝对的0卡)
还不明白的那就去链接这里自己多试几次
AVL树的查找时间复杂度为O(log n)具体推导过程可以自行网上查一查
但AVL树有个问题,我查找起来是比BTS的极端情况快了很多 但我插入删除左旋转右旋转太麻烦了
怎么办?
为何不使用红黑树(Red/Black Tree)
先贴概念红黑树wiki
其他红黑的概念暂时不提
重点:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
也就是说 之前AVL必须保证最长路径与最短路径差距小于等于1,现在变成两倍了
那么就减少了他插入/删除时一定的旋转次数
就比如插入[1,2,3,4,5,6]
AVL需要旋转3次 而红黑只需要旋转2次 数据量大则会体现的更明显
其时间复杂度同样也是O(log n)
但是如果使用红黑树仍会存在一个问题,那便是数据量过大会导致树的高度过高,是需要比较的次数过多,而每次比较便是一次磁盘的IO,要是找一个深一点的元素那得等麻了。
B树(B-Tree)
重点:B树,概括来说是一个一般化的二叉查找树(binary search tree)一个节点可以拥有2个以上的子节点
因为二叉树会导致层数过高 那么我增加树的一个节点的可以存放数据的量再多加几个分出去的叉就能让层数有效减少了啊
先看看B树的几个特点
一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树,或者是满足下列性质的树:
根结点至少有两个子女;
每个非根节点所包含的关键字个数 j 满足:┌m/2┐ - 1 <= j <= m - 1;
除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足:┌m/2┐ <= k <= m ;
所有的叶子结点都位于同一层。
好,以一个阶(度)为5的B树为例
翻译一下上面的话
根节点内的元素个数区间[1,4] (1≤ 元素个数 ≤ 4 后面就不翻译了 )
根节点的子节点(分叉线)个数区间[2,5]
内节点(就是介于最上层与最下层之间的节点)的子节点(分叉线)个数区间[3,5]
非根节点内元素个数区间[2,4]
然后来插入 [1,2,3,4,5]
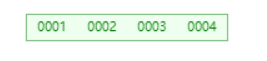
插入1-4时会同为一个根节点
继续插入5时因为超过根节点内元素个数从而将中间数3取出作为新的根节点 【1,2】【4,5】作为他的两个子节点
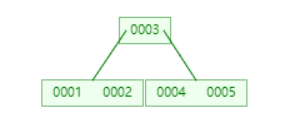
继续往下插入
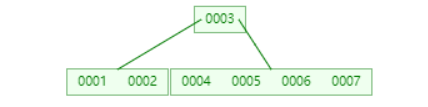
插入到8时则会再次取中间数6分裂为两个子节点再将6与父节点3合并 注意看具体线引出的位置
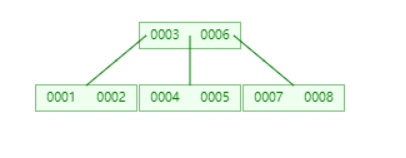
这个分叉的线实际为指针指向,也是要占用空间的 其保证 3与6之间的子节点的元素值区间为(3 , 6)
B树其他的便特性便先不讲
先看看B+树的特性而后再说为何mysql会使用B+树做索引
B+树
B+树其实是B树的一种改进版 B+树wiki 与 B+树百度百科
重点特性
每个结点至多有m个子女;
除根结点外,每个结点至少有[m/2]个子女,根结点至少有两个子女;
有k个子女的结点必有k个关键字。
同样以度为5的B+树为例
插入1-5是是这样的
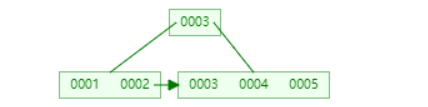
可以看到与B树不同的是他将3存入了叶子节点
而查找3时不同于B树 B+树会先找到根节点3而后向右子节点查找 找到在叶子节点中的3再返回
那么问题来了 这样看来这B树不是更适合B+树?
那么来看最后的结论
为何是B+而不是B
由于实际的mysql中我们是一条一条的记录,那么不止数字那么简单
比如我们假设一个磁盘块为32K大小
我们假设一个索引数字为1k,一条指针为1k(实际不会这么大只是方便演示),一条数据为4k
那么如果我们用B树来存储
那么一个磁盘块最多只能存储5条数据 (4+1)*5 + 6 = 31
如下图所示
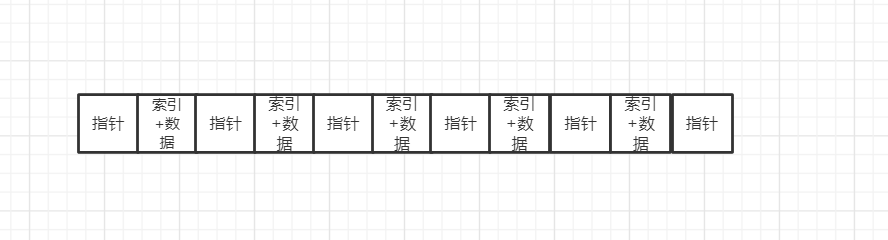
那么如果树高为3 那么一共能存储
5 * 6^0 + 5 * 6^1 + 5*6^2 = 95条数据
那么我们看看B+树能存多少
由于只存索引那么一行可以存下15条索引+16条指针
那么树高为3 在第三行一共有16*16(256)个磁盘块 可以存储数据
估算一下肯定远高于B树能存下的95条数据
实际上InnoDB一颗B+树可以存放2kw条数据(当然取决于你主键类型)
所以这就是为何选用B+树而不是B树的原因
那么问题又来了
为何会用B+树而不是用跳表呢?
那为何redis又使用了跳表而mysql使用B+树呢
我还没复习到redis 下次一定说
下次一定说
本作品采用《CC 协议》,转载必须注明作者和本文链接





 关于 LearnKu
关于 LearnKu



