2022-12-10:给你一个由小写字母组成的字符串 s ,和一个整数 k 如果满足下述条件
2022-12-10:给你一个由小写字母组成的字符串 s ,和一个整数 k
如果满足下述条件,则可以将字符串 t 视作是 理想字符串 :
t 是字符串 s 的一个子序列。
t 中每两个 相邻 字母在字母表中位次的绝对差值小于或等于 k 。
返回 最长 理想字符串的长度。
字符串的子序列同样是一个字符串,并且子序列还满足:
可以经由其他字符串删除某些字符(也可以不删除)但不改变剩余字符的顺序得到。
注意:字母表顺序不会循环
例如,’a’ 和 ‘z’ 在字母表中位次的绝对差值是 25,而不是 1 。
答案2022-12-10:
二维动态规划的解。
N为字符串长度,E为字符集大小,K为差值要求。
时间复杂度O(NE)。
空间复杂度O(NE)。
一维动态规划从左往右递推版。
N为字符串长度,E为字符集大小,K为差值要求。
时间复杂度O(N*K)。
空间复杂度O(E)。
从左往右递推 + 线段树优化。
N为字符串长度,E为字符集大小,K为差值要求。
时间复杂度O(N * logE)。
空间复杂度O(E)。
代码用rust编写。代码如下:
use std::iter::repeat;
fn main() {
let s = "acfgbd";
let k = 2;
let ans = longest_ideal_string1(s, k);
println!("ans = {}", ans);
let ans = longest_ideal_string2(s, k);
println!("ans = {}", ans);
let ans = longest_ideal_string3(s, k);
println!("ans = {}", ans);
}
// 二维动态规划的解
// N为字符串长度,E为字符集大小,K为差值要求
// 时间复杂度O(N*E)
// 空间复杂度O(N*E)
fn longest_ideal_string1(s: &str, k: i32) -> i32 {
let ss: Vec<char> = s.chars().collect();
let n = s.len() as i32;
let mut arr: Vec<i32> = repeat(0).take(n as usize).collect();
for i in 0..n {
arr[i as usize] = ss[i as usize] as i32 - 'a' as i32;
}
let mut dp: Vec<[i32; 27]> = repeat([-1; 27]).take(n as usize).collect();
return f(&mut arr, 0, 26, k, &mut dp);
}
fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
if a > b {
a
} else {
b
}
}
fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
if a < b {
a
} else {
b
}
}
// 数组s中所有的值都在0~25对应a~z
// 当前在s[i...]选择数字, 并且前一个数字是p
// 如果p<26,说明选择的前一个数字是p
// 如果p==26,说明之前没有选过任何数字
// 返回在前一个数字是p的情况下,在s[i...]上选择数字,最长理想子序列能是多长
// dp仅仅是缓存结构,暴力递归改动态规划常规技巧
fn f(s: &mut Vec<i32>, i: i32, p: i32, k: i32, dp: &mut Vec<[i32; 27]>) -> i32 {
if i == s.len() as i32 {
return 0;
}
if dp[i as usize][p as usize] != -1 {
return dp[i as usize][p as usize];
}
let p1 = f(s, i + 1, p, k, dp);
let mut p2 = 0;
if (p == 26 || i32::abs(s[i as usize] - p) <= k) {
p2 = 1 + f(s, i + 1, s[i as usize], k, dp);
}
let ans = get_max(p1, p2);
dp[i as usize][p as usize] = ans;
return ans;
}
// 一维动态规划从左往右递推版
// N为字符串长度,E为字符集大小,K为差值要求
// 时间复杂度O(N*K)
// 空间复杂度O(E)
fn longest_ideal_string2(s: &str, k: i32) -> i32 {
let mut dp: [i32; 26] = [0; 26];
let mut c = 0;
let mut l = 0;
let mut r = 0;
let mut pre = 0;
let mut ans = 0;
let ss: Vec<char> = s.chars().collect();
for i in 0..ss.len() {
c = ss[i as usize] as i32 - 'a' as i32;
l = get_max(c - k, 0);
r = get_min(c + k, 25);
pre = 0;
for j in l..=r {
pre = get_max(pre, dp[j as usize]);
}
dp[c as usize] = 1 + pre;
ans = get_max(ans, dp[c as usize]);
}
return ans;
}
// 从左往右递推 + 线段树优化
// N为字符串长度,E为字符集大小,K为差值要求
// 时间复杂度O(N * logE)
// 空间复杂度O(E)
fn longest_ideal_string3(s: &str, k: i32) -> i32 {
let ss: Vec<char> = s.chars().collect();
// 0 0 0
// 1(a) 2(b) ... 26(z)
let mut st = SegmentTree::new(26);
let mut c = 0;
let mut pre = 0;
let mut ans = 0;
for i in 0..ss.len() {
// i s.charAt(i)
// a 1
// b 2
// z 26
c = ss[i as usize] as i32 - 'a' as i32 + 1;
// 2 k = 3
// 1 2 3 4 5 6 7
// l = Math.max(c - k, 1)
// r = Math.min(c + k, 26)
pre = st.max(get_max(c - k, 1), get_min(c + k, 26));
ans = get_max(ans, 1 + pre);
st.update(c, 1 + pre);
}
return ans;
}
struct SegmentTree {
n: i32,
max: Vec<i32>,
}
impl SegmentTree {
fn new(maxSize: i32) -> Self {
let max: Vec<i32> = repeat(0).take(((maxSize + 1) << 2) as usize).collect();
SegmentTree {
n: maxSize + 1,
max,
}
}
fn update(&mut self, index: i32, c: i32) {
self.update0(index, index, c, 1, self.n, 1);
}
fn max(&mut self, left: i32, right: i32) -> i32 {
return self.max0(left, right, 1, self.n, 1);
}
fn pushUp(&mut self, rt: i32) {
self.max[rt as usize] = get_max(
self.max[(rt << 1) as usize],
self.max[(rt << 1 | 1) as usize],
);
}
fn update0(&mut self, L: i32, R: i32, C: i32, l: i32, r: i32, rt: i32) {
if L <= l && r <= R {
self.max[rt as usize] = C;
return;
}
let mid = (l + r) >> 1;
if (L <= mid) {
self.update0(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
self.update0(L, R, C, mid + 1, r, rt << 1 | 1);
}
self.pushUp(rt);
}
fn max0(&mut self, L: i32, R: i32, l: i32, r: i32, rt: i32) -> i32 {
if L <= l && r <= R {
return self.max[rt as usize];
}
let mut mid = (l + r) >> 1;
let mut ans = 0;
if (L <= mid) {
ans = get_max(ans, self.max0(L, R, l, mid, rt << 1));
}
if R > mid {
ans = get_max(ans, self.max0(L, R, mid + 1, r, rt << 1 | 1));
}
return ans;
}
}
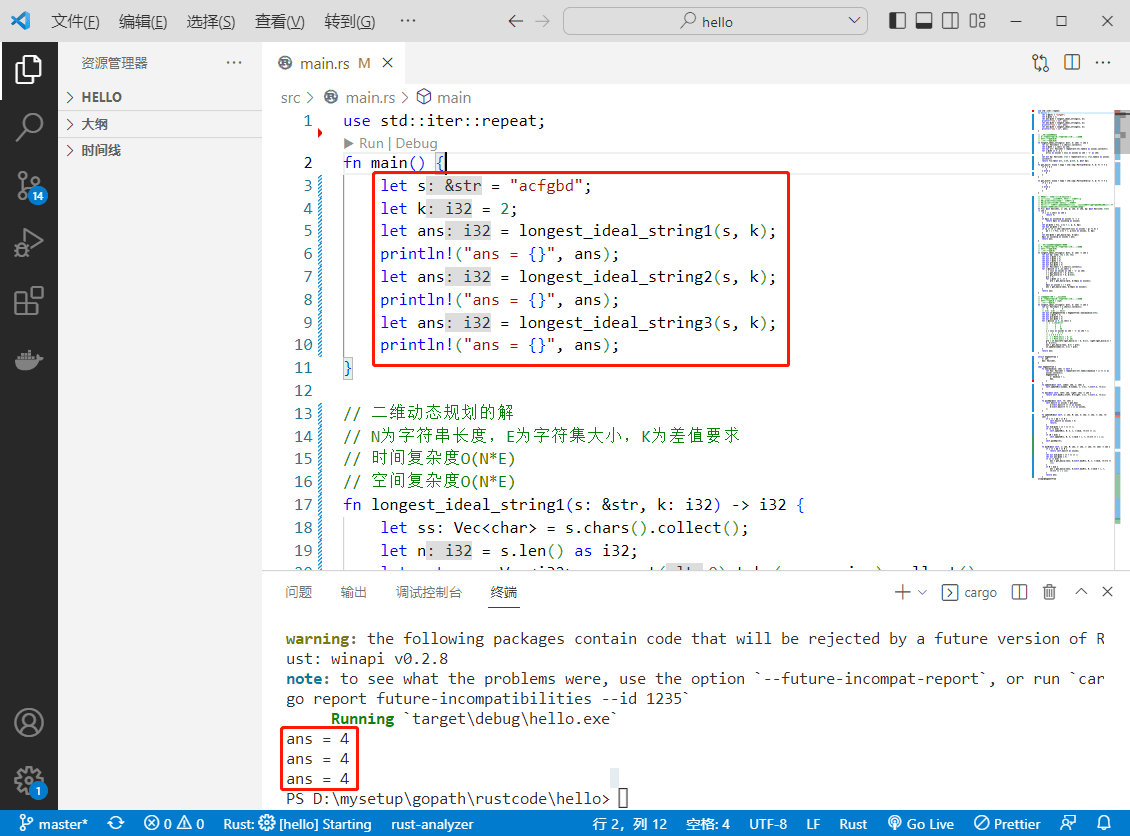
执行结果如下:
本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu



