剪绳子

题目描述

给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1，m<=n），每段绳子的长度记为k[1],…,k[m]。请问k[1]x…xk[m]可能的最大乘积是多少？
例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例

输入一个数n，意义见题面。（2 <= n <= 60）

8

返回值

18

分析

假设绳子长度为 4,那么在绳子位置为 1、2、3 处剪一刀的可能。

• 在位置为 1 处剪一刀，剩下绳长为 (4-1)=3，如图标注 A。
• 3 有两种情况：继续剪或者不剪。继续剪的话在绳长为 3 的位置 1、2 处剪的可能。

• 在 1 处剪，剩下 2，如图标注 B，可以选择继续剪或者不剪，取最大值。

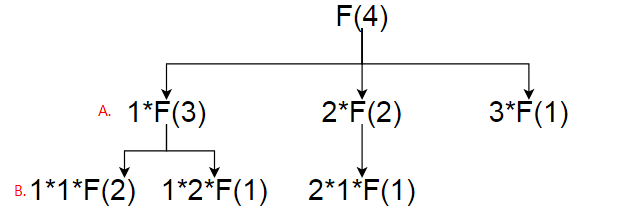
解法一：动态规划

状态转移方程： 其中 1 < j < i

<?php

namespace app\controller;

class Index
{
    /**
     * 动态规划
     * 时间:O(N²) 空间：O(N)
     * @param int number 绳长
     * @return int
     */
    public function cutRope($number)
    {
        $dp = [0, 1, 1, 2];                   // dp[i] 表示绳长 i 剪短后的最大乘积。
        if ($number < 4) return $dp[$number]; // 绳长小于 4 ，直接返回值。

        for ($i = 4; $i <= $number; $i++) {   // 从绳长为 4 开始
            $dp[$i] = 0;                      // 先初始值，否则下一个循环报错：未定义索引
            for ($j = 1; $j < $i; $j++) {     // 从 1 处开始再剪一刀
                $dp[$i] = max($dp[$i], max($j * ($i - $j), $j * $dp[$i - $j]));
            }
        }
        return $dp[$number];
    }
}

解法二：贪心算法

• 当 n >= 5时,将它剪成 2 或 3 的绳子段,2 * (n-2) > n,3 * (n-3) > n,都大于他未拆分前的情况，且3 * (n-3) >= 2 * (n-2),所以我们尽可能地多剪 3 的绳子段。
• 当绳子长度为 4 时比较特殊，2 * 2 > 1 * 3,所以没必要继续剪。

<?php

namespace app\controller;

class Index
{
    /**
     * 贪心算法
     * 时间:O(1) 空间：O(1)
     * @param int number 绳长
     * @return int
     */
    public function cutRope($n)
    {
        if ($n < 4) return $n - 1;                // 如果小于 4 ，直接返回：值-1。

        $timesOf3 = intdiv($n, 3);                // 尽可能剪成长度为 3 绳子
        if ($n - $timesOf3 * 3 == 1) $timesOf3--; // 如果最后剩 4 ，则剪成 2 * 2
        $timesOf2 = intdiv($n - $timesOf3 * 3, 2);

        // (剪成 3 的乘积) * (剪成 2 的乘积)
        return pow(3, $timesOf3) * pow(2, $timesOf2);
    }
}