二叉搜索树的第k个节点

题目描述

给定一棵二叉搜索树，请找出其中的第k小的结点。

示例

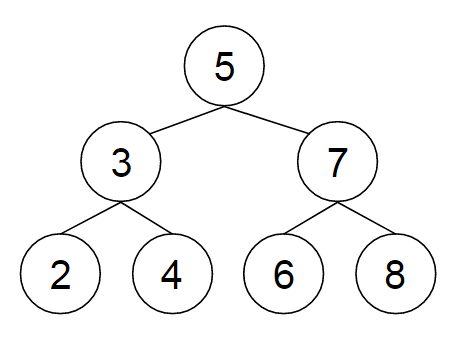
输入

{5,3,7,2,4,6,8},3

返回值

{4}

分析

二叉搜索树的特性是根节点比左节点大，但是比右节点小，而中序遍历符合这个特性。

解法一：中序遍历

中序遍历二叉搜索树的所有节点，放入数组，最后数组索引k-1即第 k 小节点。

class TreeNode{
    var $val;
    var $left  = NULL;
    var $right = NULL;

    function __construct($val){
        $this->val = $val;
    }
}

<?php

namespace app\controller;

class Index
{
    /**
     * 中序遍历
     */
    public function LDR($pRoot, &$list)
    {
        if ($pRoot == null) return null;

        $this->LDR($pRoot->left, $list);
        $list[] = $pRoot;
        $this->LDR($pRoot->right, $list);
        return $list;
    }
}

    /**
     * 测试
     */
    public function test()
    {
        // 构造二叉搜索树
        $root  = new TreeNode(5);
        $node3 = new TreeNode(3);
        $node7 = new TreeNode(7);
        $node2 = new TreeNode(2);
        $node4 = new TreeNode(4);
        $node6 = new TreeNode(6);
        $node8 = new TreeNode(8);

        $root->left  = $node3;
        $root->right = $node7;
        $node3->left  = $node2;
        $node3->right = $node4;
        $node7->left  = $node6;
        $node7->right = $node8;

        $k    = 3;  // 第 k 小节点
        $list = []; // 存放中序遍历节点

        $this->LDR($root, $list);
        echo $list[$k - 1];
    }

解法二：优化中序遍历

解法一中需要遍历所有节点，最后再取出索引为k-1的值。
优化：利用变量$k，计算已遍历的节点数，当遍历 k 个节点，直接返回值。

<?php

namespace app\controller;

class Index
{
    /**
     * 中序遍历优化
     */
    public function KthNode($pRoot, &$k)
    {
        if (!$pRoot) return null;

        $t = $this->KthNode($pRoot->left, $k);  // 递归到最左节点
        if ($t) return $t;                      // 如果上一行代码在递归中满足(--$k==0)，则 $t不为 null。
        if (--$k == 0) return $pRoot;           // 判断是否递归到第 k 个节点

        $t = $this->KthNode($pRoot->right, $k); // 递归右节点
        if ($t) return $t;
    }
}

测试

    /**
     * 测试
     */
    public function test()
    {
        $root  = new TreeNode(5);
        $node3 = new TreeNode(3);
        $node7 = new TreeNode(7);
        $node2 = new TreeNode(2);
        $node4 = new TreeNode(4);
        $node6 = new TreeNode(6);
        $node8 = new TreeNode(8);

        $root->left   = $node3;
        $root->right  = $node7;
        $node3->left  = $node2;
        $node3->right = $node4;
        $node7->left  = $node6;
        $node7->right = $node8;

        $k   = 1;
        $res = $this->KthNode($root, $k);
        print_r($res);
    }