叉积（外积）

叉积

叉积，又叫做外积。设想一下两个向量在一个三维空间里的场景：

\displaystyle \vec{A}=\langle a_1,a_2,a_3\rangle\\{}\\ \vec{B}=\langle b_1,b_2,b_3\rangle

叉积定义

\displaystyle \vec{A}\times\vec{B}= \left|\begin{array}{c} \hat{i} & \hat{j} & \hat{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{array}\right|\\{}\\ =\left|\begin{array}{c} a_2 & a_3\\ b_2 & b_3 \end{array}\right|\hat{i} -\left|\begin{array}{c} a_1 & a_3\\ b_1 & b_3 \end{array}\right|\hat{j} +\left|\begin{array}{c} a_1 & a_2\\ b_1 & b_2 \end{array}\right|\hat{k}

叉积最终得到的还是向量。
两个向量叉积的模长等于这两个向量形成的平行四边形的面积

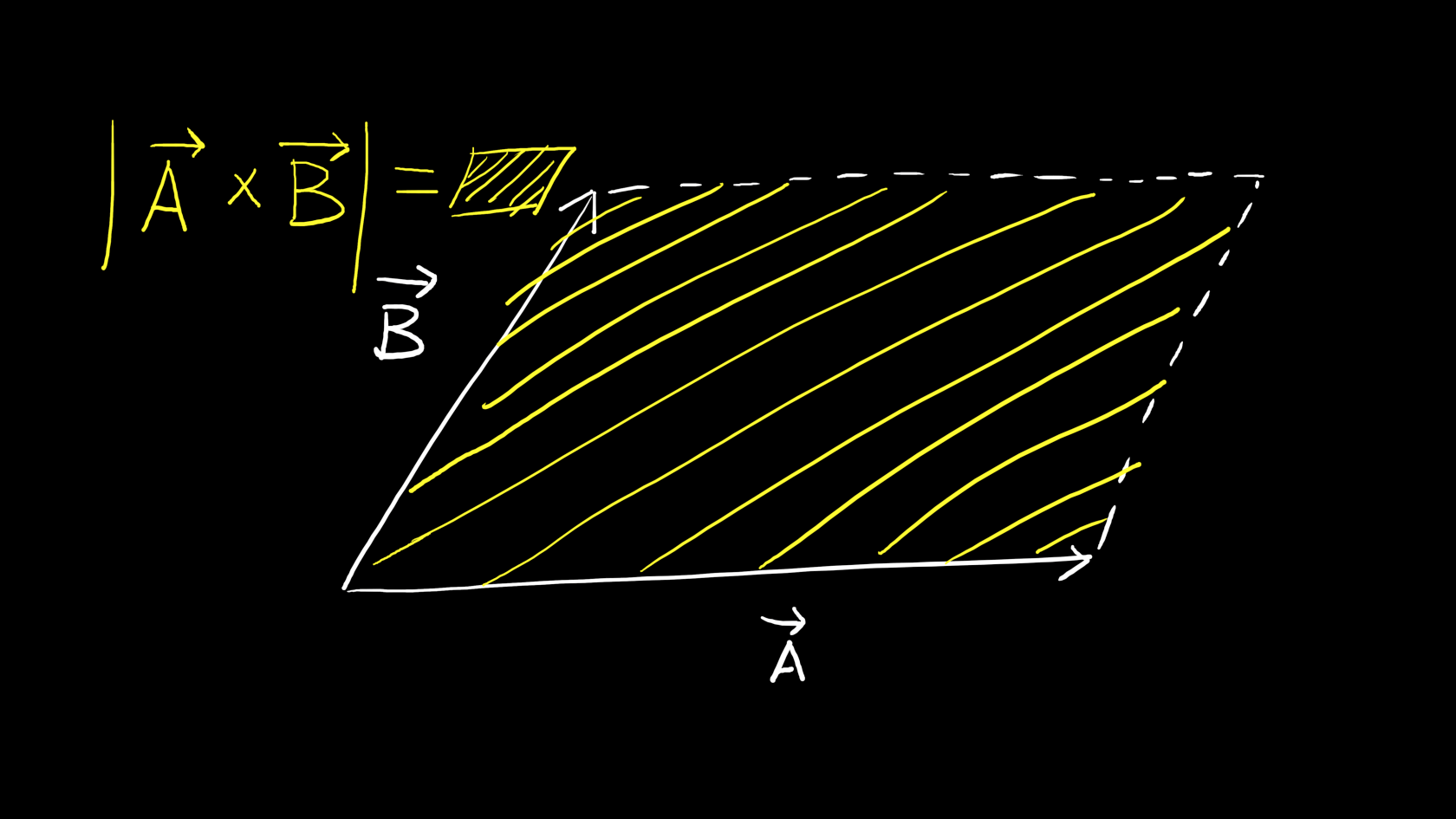
两个向量叉积的方向正交（垂直）于两个向量所构成平面

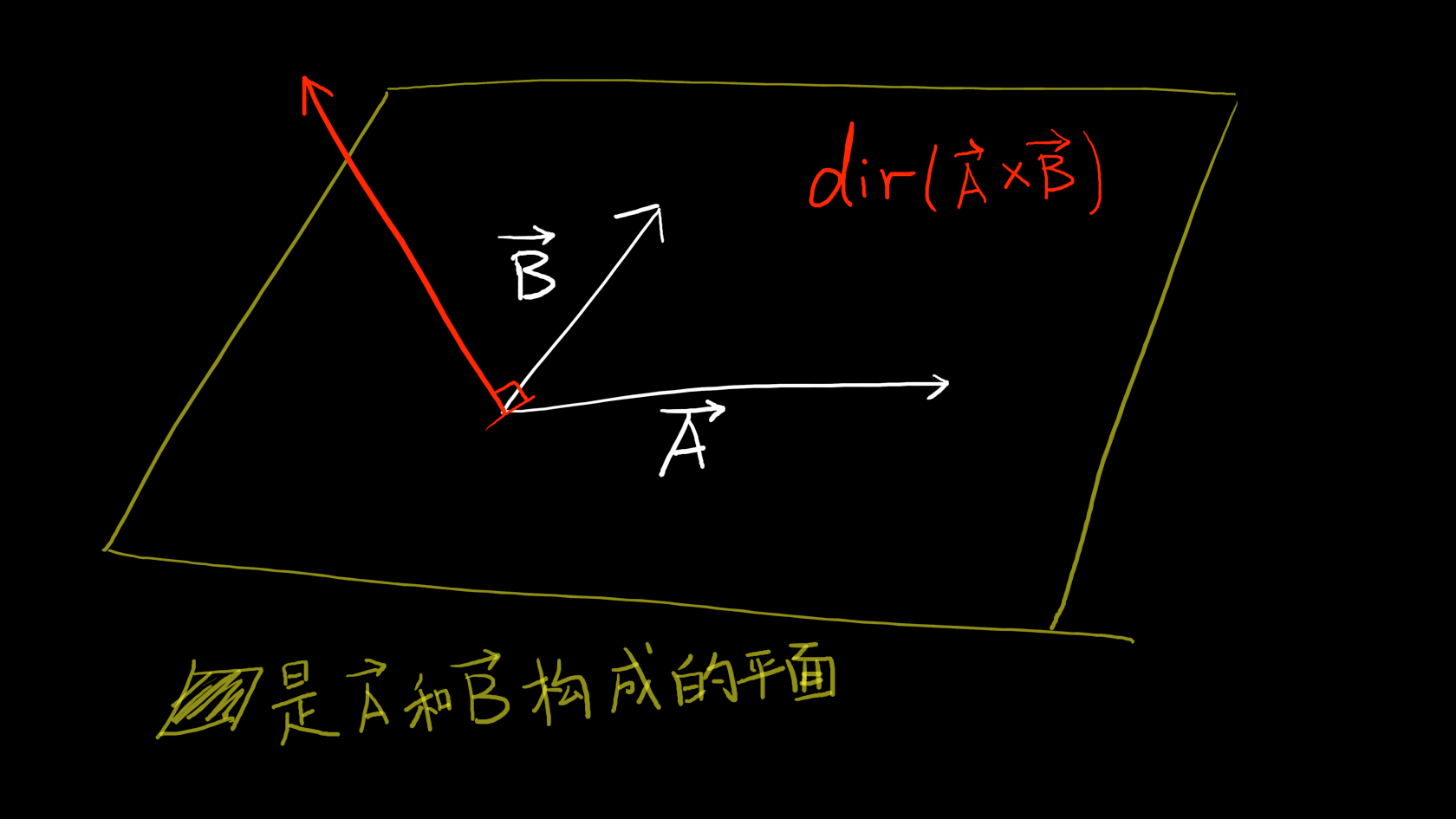
但是如何判断这个向量的方向是在上面还是在下面呢？这个可以用“右手定则”，右手定则是一个小技巧，首先伸出右手，把手指全部摊平，食指指向\vec{A}箭头的方向，然后弯曲手指做到食指指向\vec{B}箭头的方向，这时候手别动，把大拇指翘起来，大拇指所指示的方向就是这个叉积后得到的向量箭头的方向。
注意第一步用食指指向的是叉乘左边的因子，第二步弯曲食指指向的是叉乘右边的因子。

叉积应用

计算由三个向量所构成的平行六面体的体积：

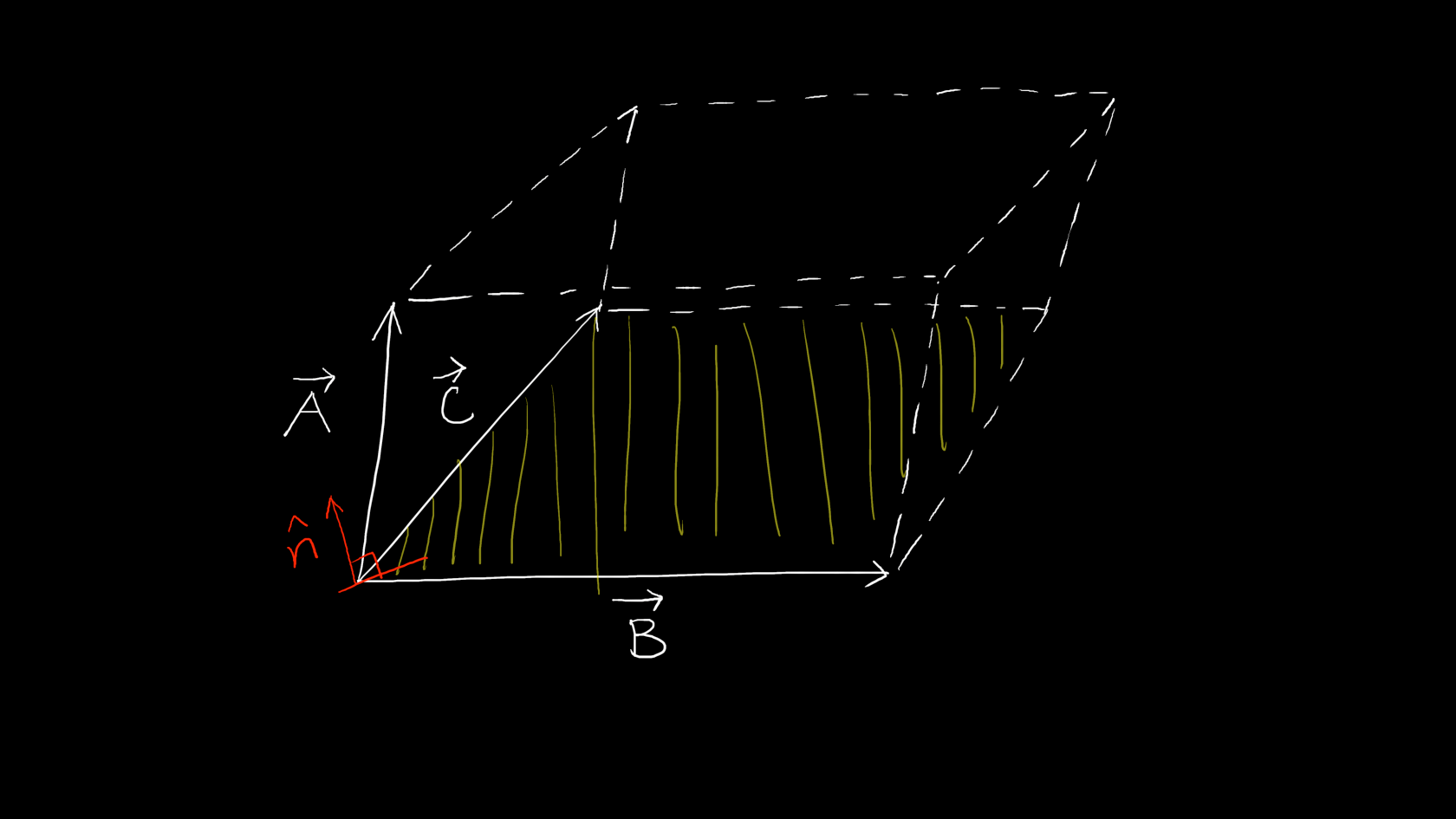
这个平行六面体的体积等于底面积乘以高，这个底面积就是|\vec{B}\times\vec{C}|，高是\vec{A}\cdot\hat{n}，是\vec{A}在方向\hat{n}上的分量。
这个分量证明可以看下图：

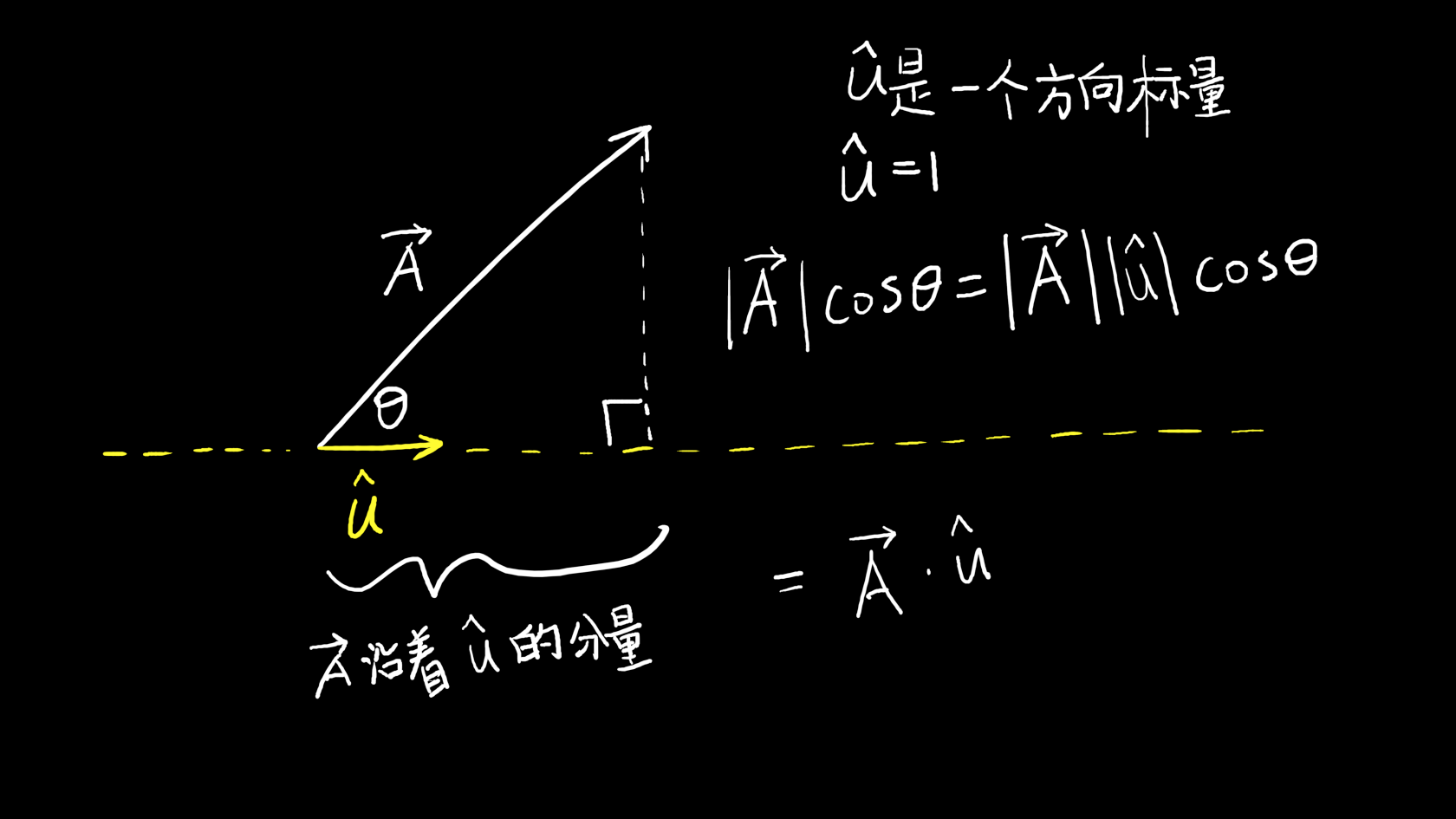
接着看\hat{n}：

\displaystyle \hat{n}=\frac{\vec{B}\times\vec{C}}{|\vec{B}\times\vec{C}|}

所以平行六面体的体积是：

\displaystyle |\vec{B}\times\vec{C}|(\vec{A}\cdot\hat{n})\\{}\\ =|\vec{B}\times\vec{C}|\left(\vec{A}\cdot\frac{\vec{B}\times\vec{C}}{|\vec{B}\times\vec{C}|}\right)\\{}\\ \therefore\ \mathrm{det}(\vec{A},\vec{B},\vec{C})=\vec{A}\cdot(\vec{B}\times\vec{C})

外积还有两个法则：

\displaystyle \vec{A}\times\vec{B}=-\vec{B}\times\vec{A}\\{}\\ \vec{A}\times\vec{A}=0

找平面方程问题：

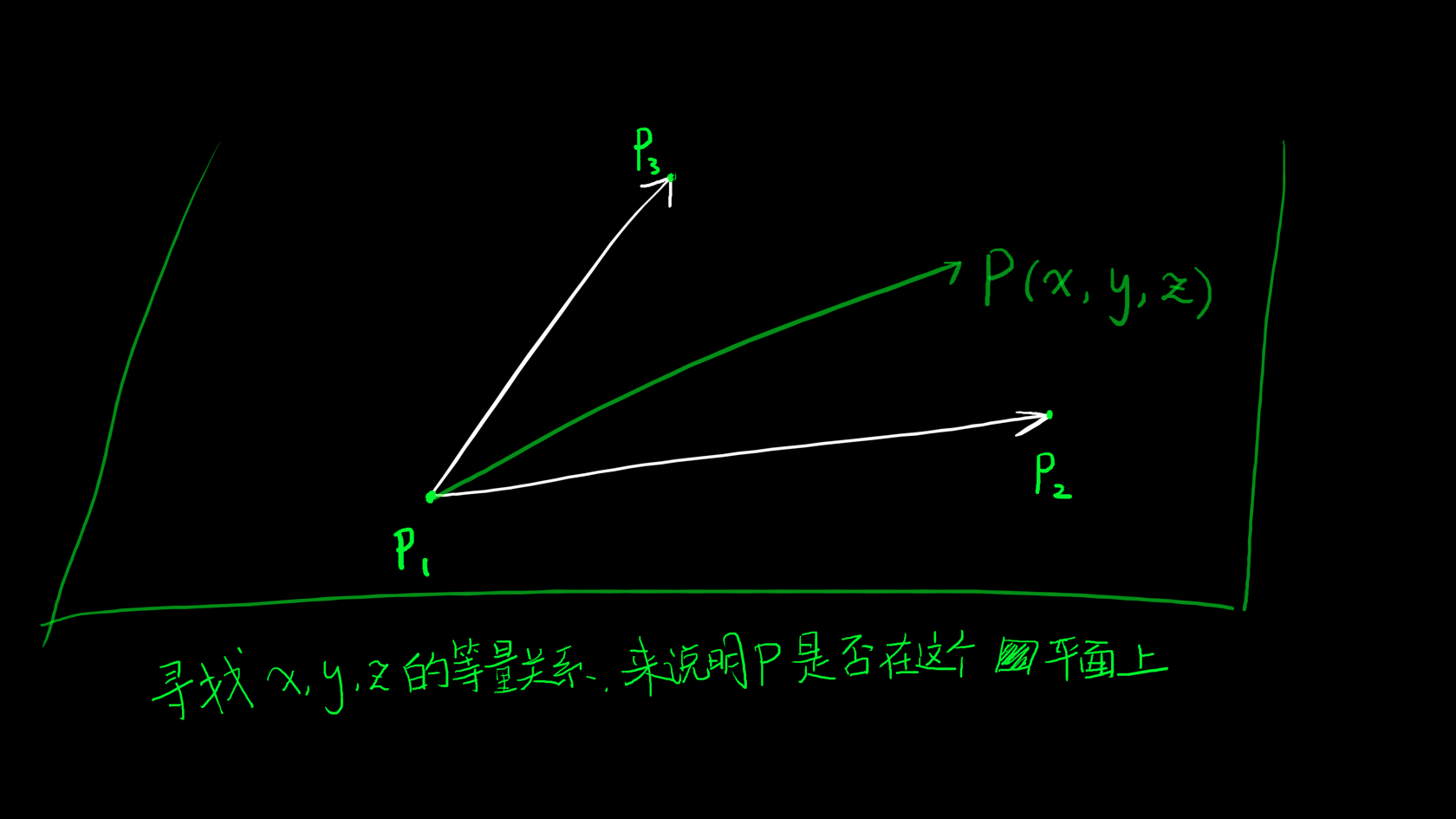
\displaystyle \mathrm{det}(\vec{P_1P},\vec{P_1P_2},\vec{P_1P_3})=0\\{}\\ \mathrm{iff}\ \vec{P_1P}\perp\vec{N}\Leftrightarrow\vec{P_1P}\cdot\vec{N}=0

其中\mathrm{iff}是当且仅当的符号，\vec{N}代表的是法向量。

\displaystyle \vec{N}=\vec{P_1P_2}\times\vec{P_1P_3}\\{}\\ \therefore\ \vec{P_1P}\cdot\vec{N}=\vec{P_1P}\cdot(\vec{P_1P_2}\times\vec{P_1P_3})