点积
前言
之前在 单变量微积分 中已经了解了两大运算,分别是微分和积分,在多变量微积分中,也是围绕这两大运算展开。只不过研究的对象不再是f(x)这样的只有一个自变量的函数,而是会研究f(x,y,z,\cdots)这样的多元函数,不过在本文档中,会着重说明两个变量的情况,可以拓展到三个变量,四个变量,n个变量,为了学习的方便,从两个变量入手最合适不过了。因为这样可以进行三维坐标系的可视化。在多变量微积分中,微分运算研究的是偏导数,积分运算研究的是多重积分。
向量
在正式进入微积分运算之前,应该先了解一点矩阵知识,如果是学过「线性代数」最好不过了,但是没学过也没关系,多变量微积分的知识里面,只需了解一些简单的矩阵知识即可,线性代数这门学科可以后面再着重攻破。
首先看图:
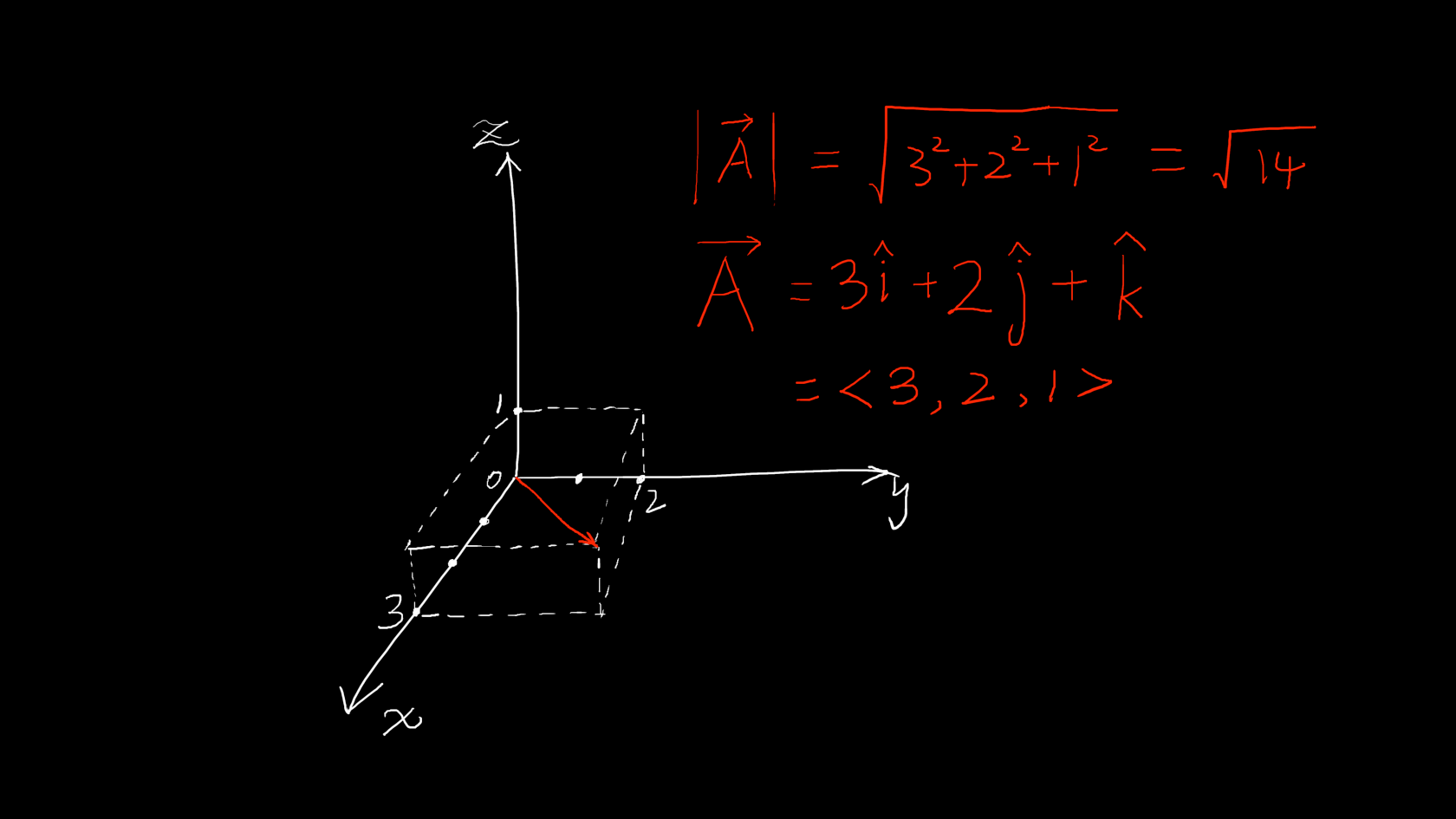
上图向量空间中的红线是一个向量,这个向量叫做\vec{A},称作“向量 A”。
给这个\vec{A}加上绝对值符号变成为了一个标量,标量代表的是向量的模长,就是一个数字。所以我们这里有向量\vec{A},以及向量的长度|\vec{A}|。向量的长度很好理解,就一个数字而已,向量呢?其实向量代表的是每个变量的刻度,上图中\vec{A}=\langle3,2,1\rangle,其中3明显就是x轴的刻度,2就是y轴的刻度,1就是z轴的刻度。每一个变量都会用一个轴来代表,如果一个函数有八个变量,那这张图就需要八个轴,就很难画出来了,八个变量的函数表示的数学模型是一个八维空间。我们在这里只画了三维空间图。
注意⚠️:别搞错了,这里可不是函数图,函数图形表示的是函数和自变量的关系,但这图只是为了解释向量的概念而作出的图形化理解。所以有三个变量表示的三个方向的三维向量空间图。这个图完全没有展现函数f(x,y,z)中f与x,y,z的关系。如果需要展现这样的函数与变量的关系,就需要四维坐标系了。三个轴做变量,一个轴做函数的值。
这里用二元函数f(x,y)举个例子,这个二元函数的函数关系图长这个样子:
其中红色阴影部分是一个平面,是一个二维的空间,只有两个方向,但给出了一个纵轴是做函数f的值的。所以以后在看图的时候一定要注意这个图代表的是否是函数图。
回到上面的话题,接着介绍一下向量和向量的长度的计算方法,向量计算公式:
\displaystyle \vec{A}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}=\langle a_1,a_2,a_3\rangle
其中\hat{i}、\hat{j}、\hat{k}代表的是方向,分别是x轴的方向,y轴的方向,z轴的方向。仅仅是方向符号。还是那句话,有多少个变量就有多少个方向。也可以说有多少个未知数就有多少个方向。a_1、a_2、a_3代表的是每个方向的刻度,也就是每个变量的值。
向量的模长计算公式:
\displaystyle |\vec{A}|=\sqrt{a_1^2+a_2^2+a_3^2}
这个可以用勾股定理的思想来理解,向量的模长等于所有变量的平方和的算术平方根。
向量的方向可以用一个数学符号代表,比如\vec{A}的方向用\mathrm{dir}(\vec{A})来表示。
向量的表示方法也可以用两个点来表示向量:
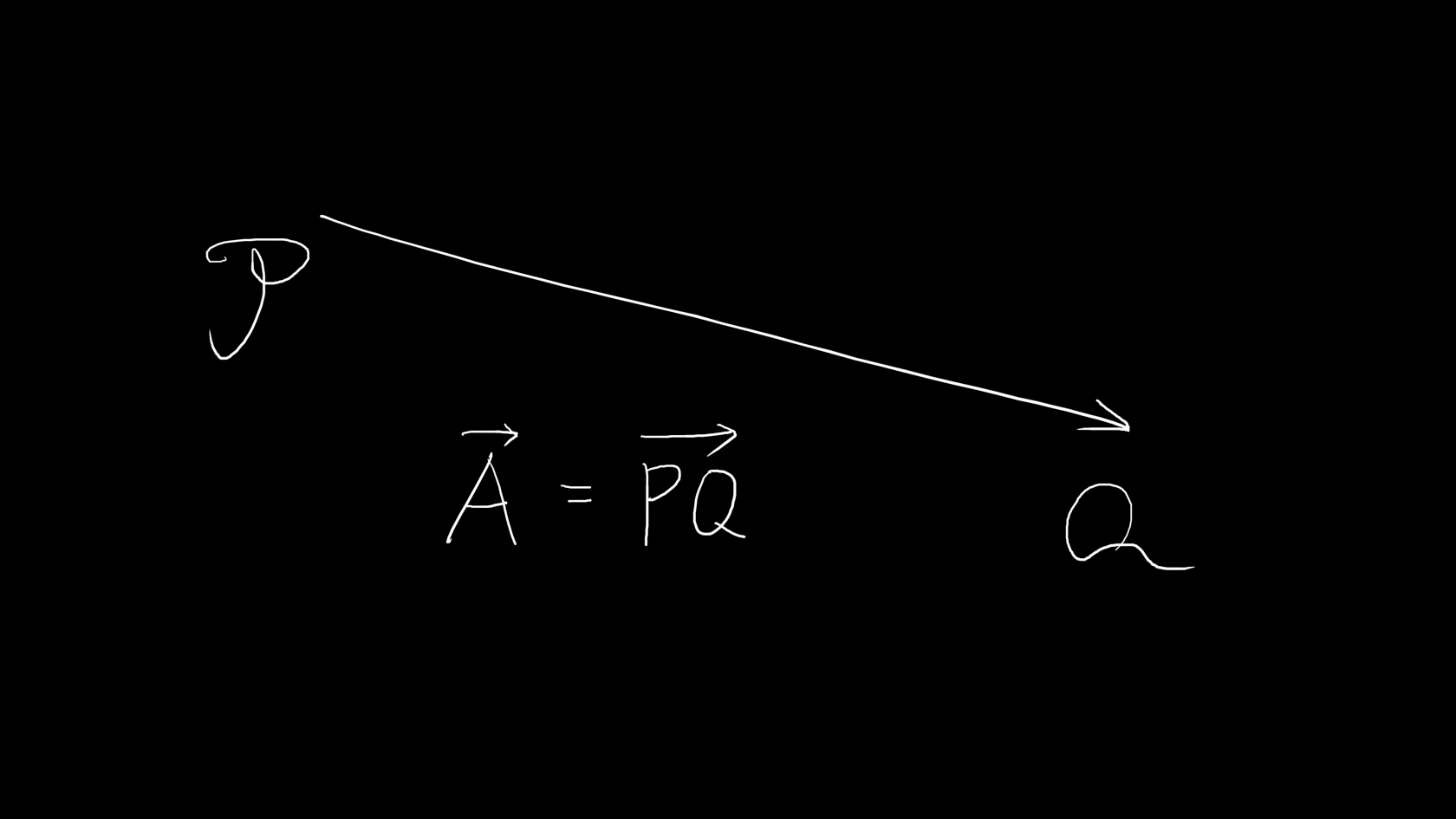
向量之和
我们习惯的看到什么什么之和这样的名词,就会想到答案会是一个数字,数字是一个标量,两个向量相加得到的还是一个向量,这个一定要切记。
看图:
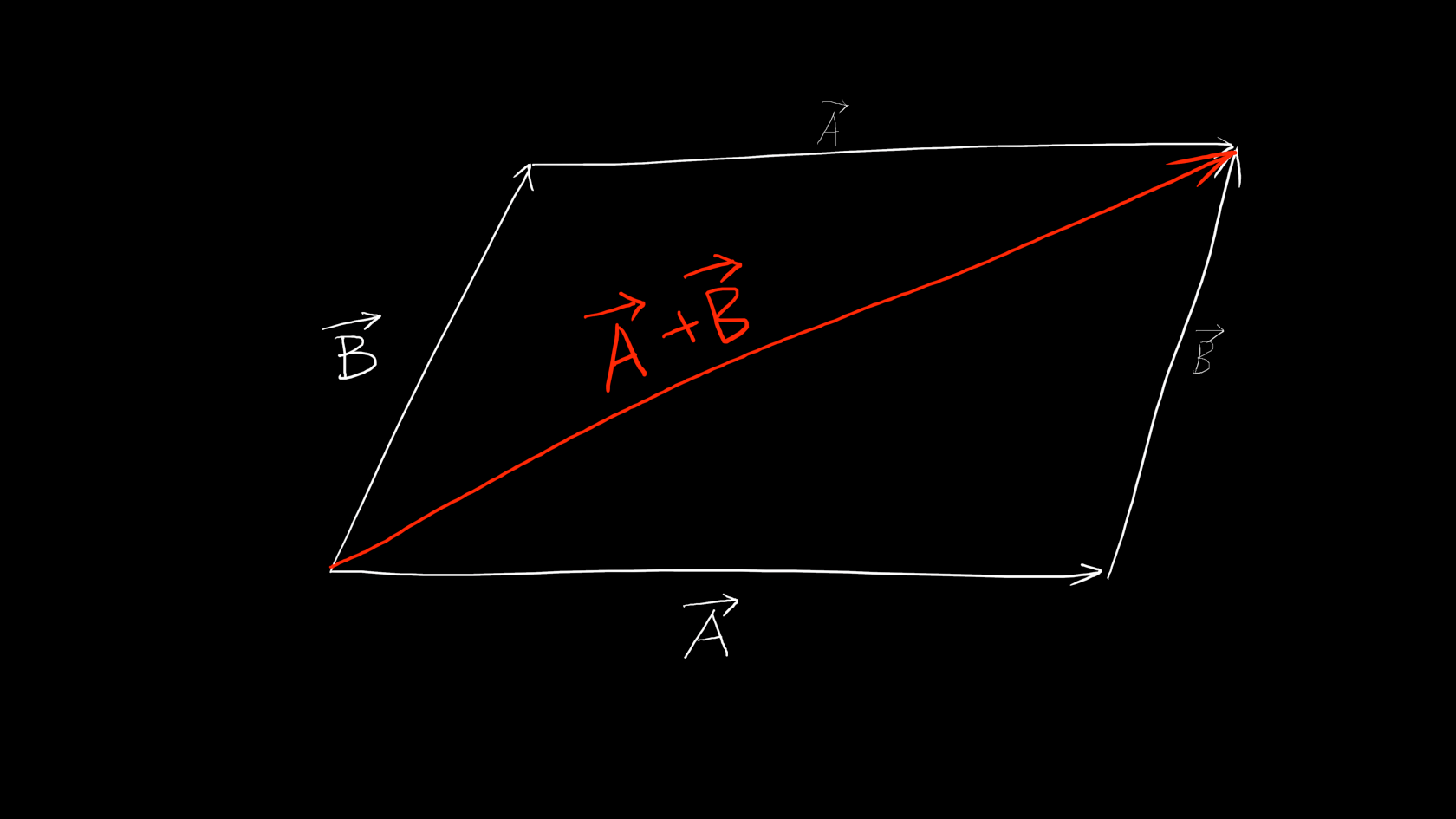
\displaystyle \vec{A}=\langle a_1,a_2,a_3\rangle\\{}\\ \vec{B}=\langle b_1,b_2,b_3\rangle\\{}\\ \vec{A}+\vec{B}=\langle a_1+b_1,a_2+b_2,a_3+b_3\rangle
向量点积(也叫做内积)
给向量一个乘法系数:
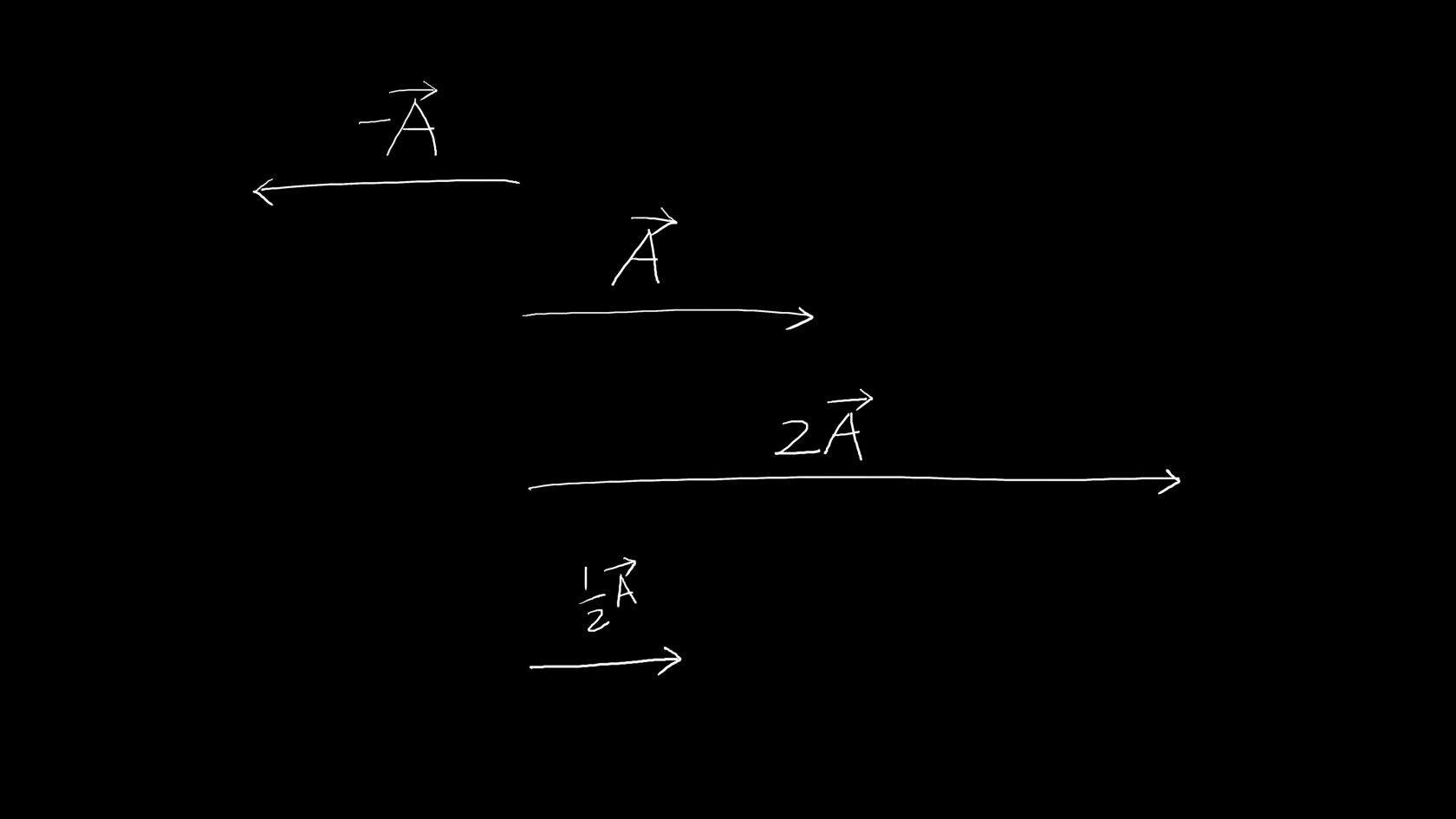
点积定义:
\displaystyle \vec{A}\cdot\vec{B}=\sum a_ib_i=a_1b_1+a_2b_2+a_3b_3
点积是两个向量相乘的一种方法,得到的是一个标量。
也就是说点积是两个向量所有对应变量的积和。
点积也可以通过另一个公式得出:
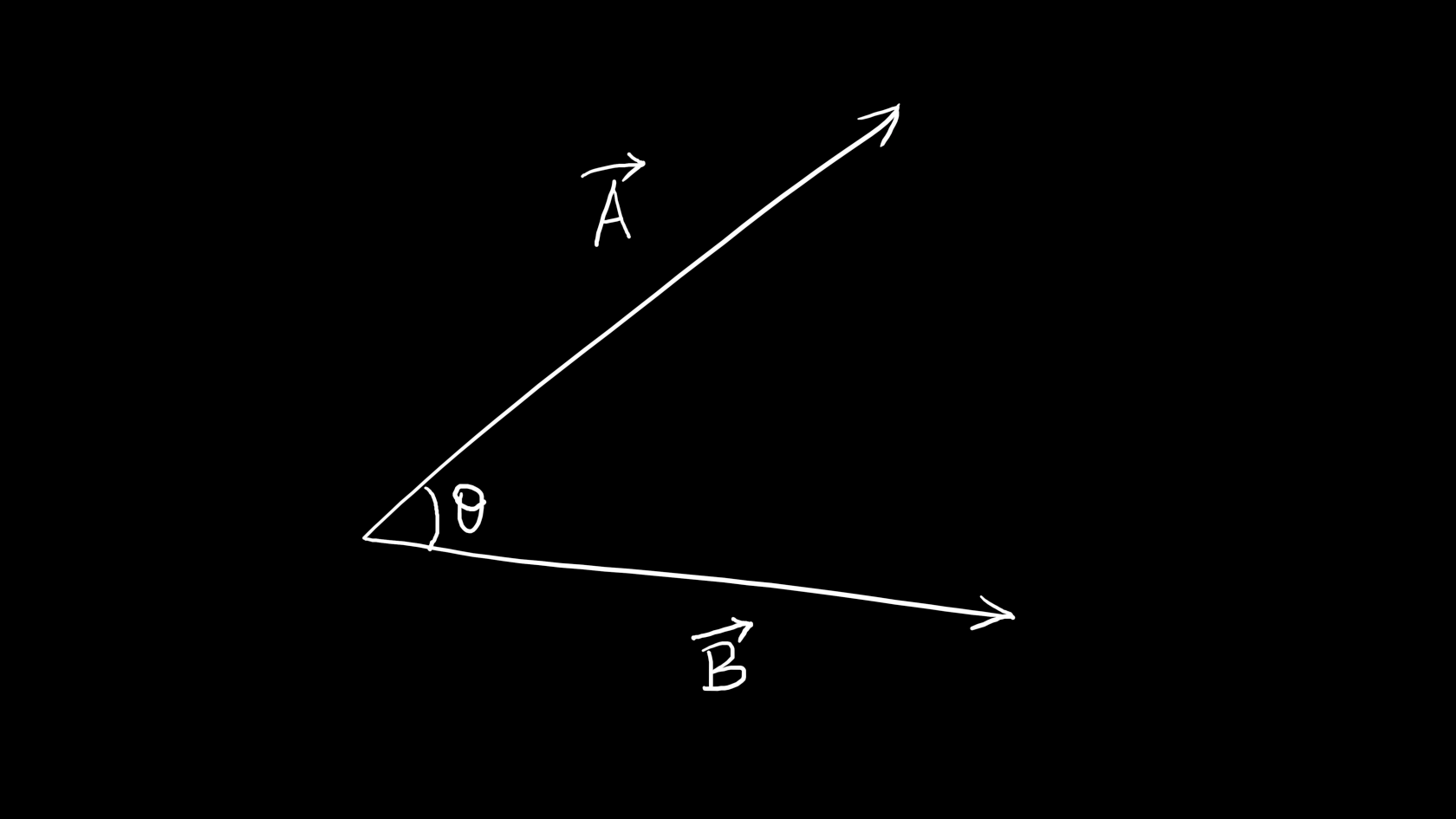
\displaystyle \vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos\theta
因为\cos0=1,可以看出:
\displaystyle \vec{A}\cdot\vec{A}=|\vec{A}|^2\cos0=a_1^2+a_2^2+a_3^2
来看下余弦定理:
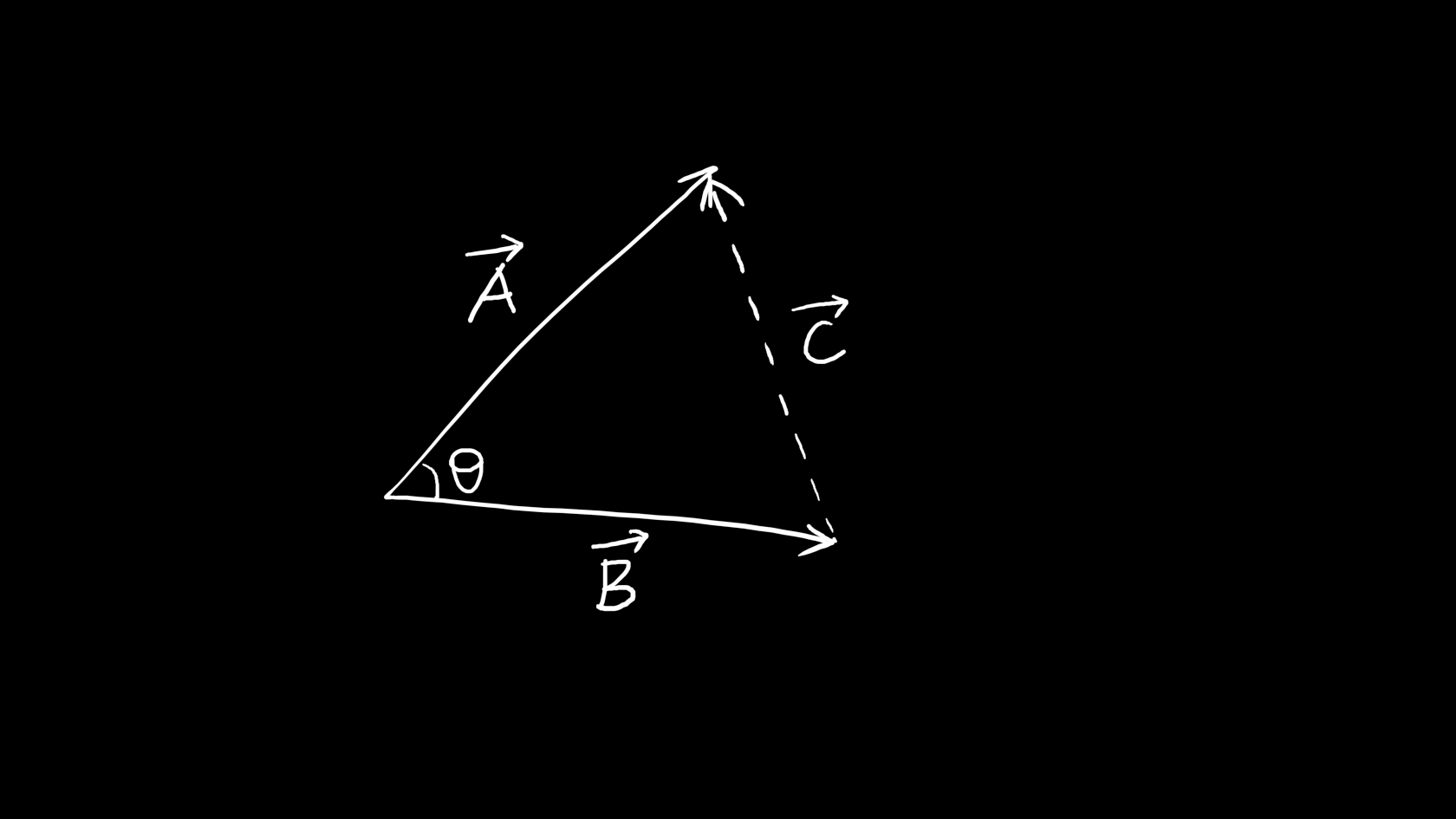
\displaystyle \vec{C}=\vec{A}-\vec{B}\\{}\\ |\vec{C}|^2=|\vec{A}|^2+|\vec{B}|^2-2|\vec{A}||\vec{B}|\cos\theta
点乘证明:
\displaystyle |\vec{C}|^2=\vec{C}\cdot\vec{C}=(\vec{A}-\vec{B})\cdot(\vec{A}-\vec{B})\\{}\\ =\vec{A}\cdot\vec{A}-\vec{A}\cdot\vec{B}-\vec{B}\cdot\vec{A}+\vec{B}\cdot\vec{B}\\{}\\ =|\vec{A}|^2+|\vec{B}|^2-2\vec{A}\cdot\vec{B}
点积应用
计算长度和角度:
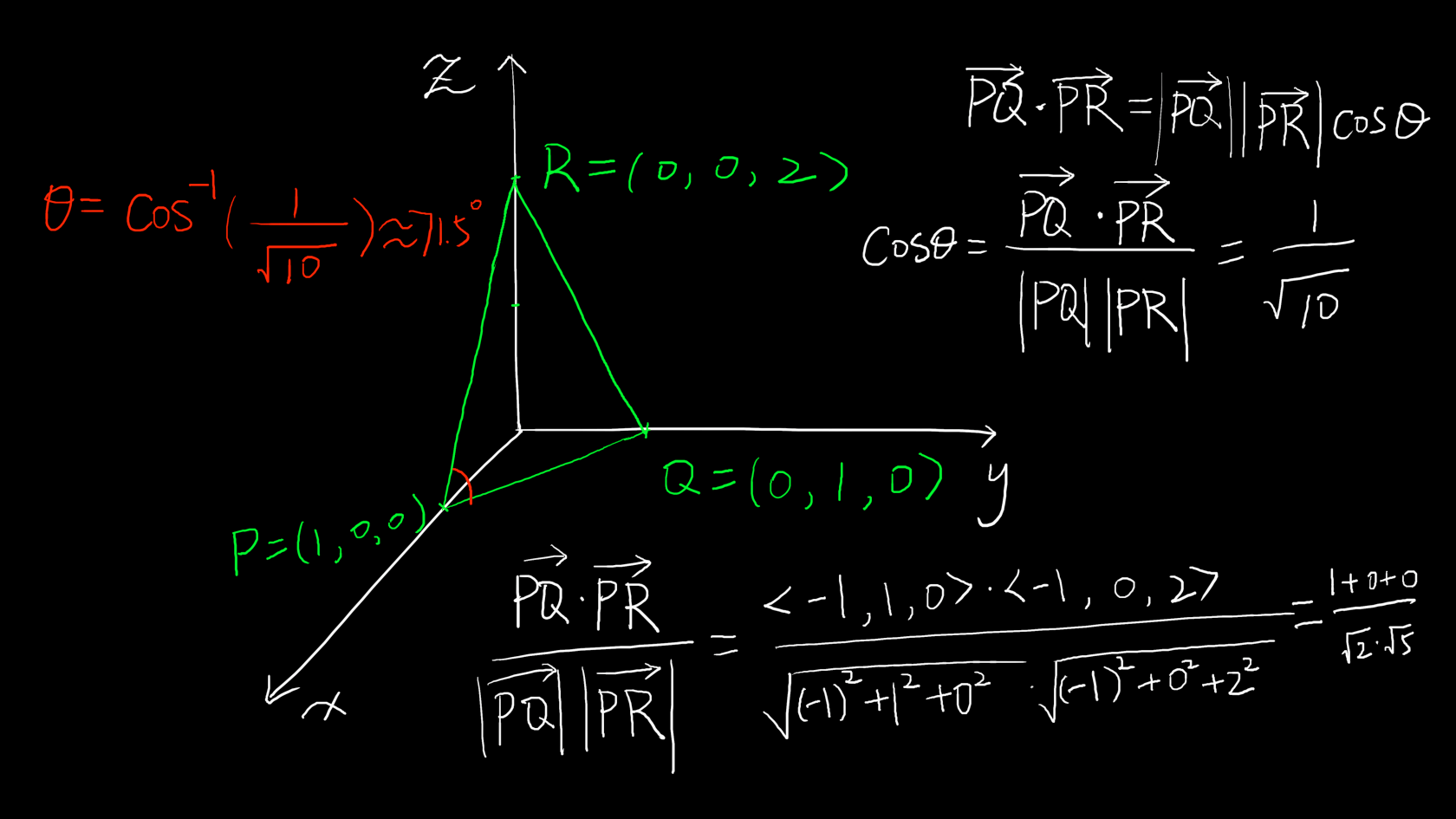
上图中有些人会对\langle-1,1,0\rangle\cdot\langle-1,0,2\rangle有疑问,因为这里得出来的是向量的值,这个向量是怎么得到的呢?
我们就看\vec{PQ}的值\langle-1,1,0\rangle,意思是通过这个向量,能从P点到Q点,所以是由Q点的坐标(q_1,q_2,q_3)减去P点的坐标(p_1,p_2,p_3)得出的。所以\langle0-1,1-0,0-0\rangle=\langle-1,1,0\rangle。
可以得出一个重要的公式:
\displaystyle \cos\theta=\frac{\vec{A}\cdot\vec{B}}{|\vec{A}||\vec{B}|}
可以通过\vec{A}\cdot\vec{B}的值来判断\theta的角度是直角还是锐角还是钝角:
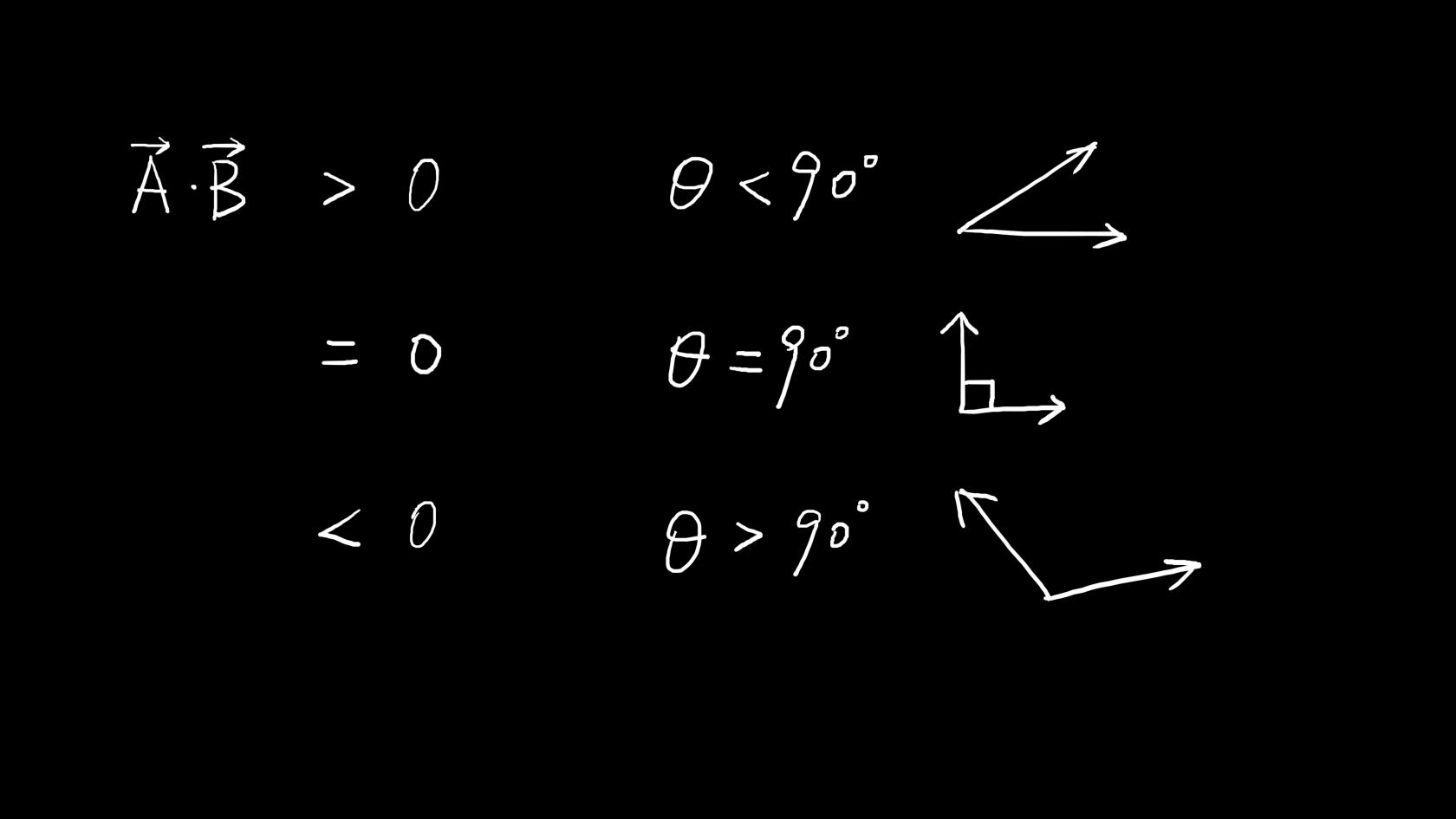
向量正交性
两个向量正交意味着它们是相互垂直的:
\displaystyle \vec{A}\cdot\vec{B}=0\Leftrightarrow\cos\theta=0\Leftrightarrow\theta=90\degree\Leftrightarrow\vec{A}\perp\vec{B}

 多变量微积分入门
多变量微积分入门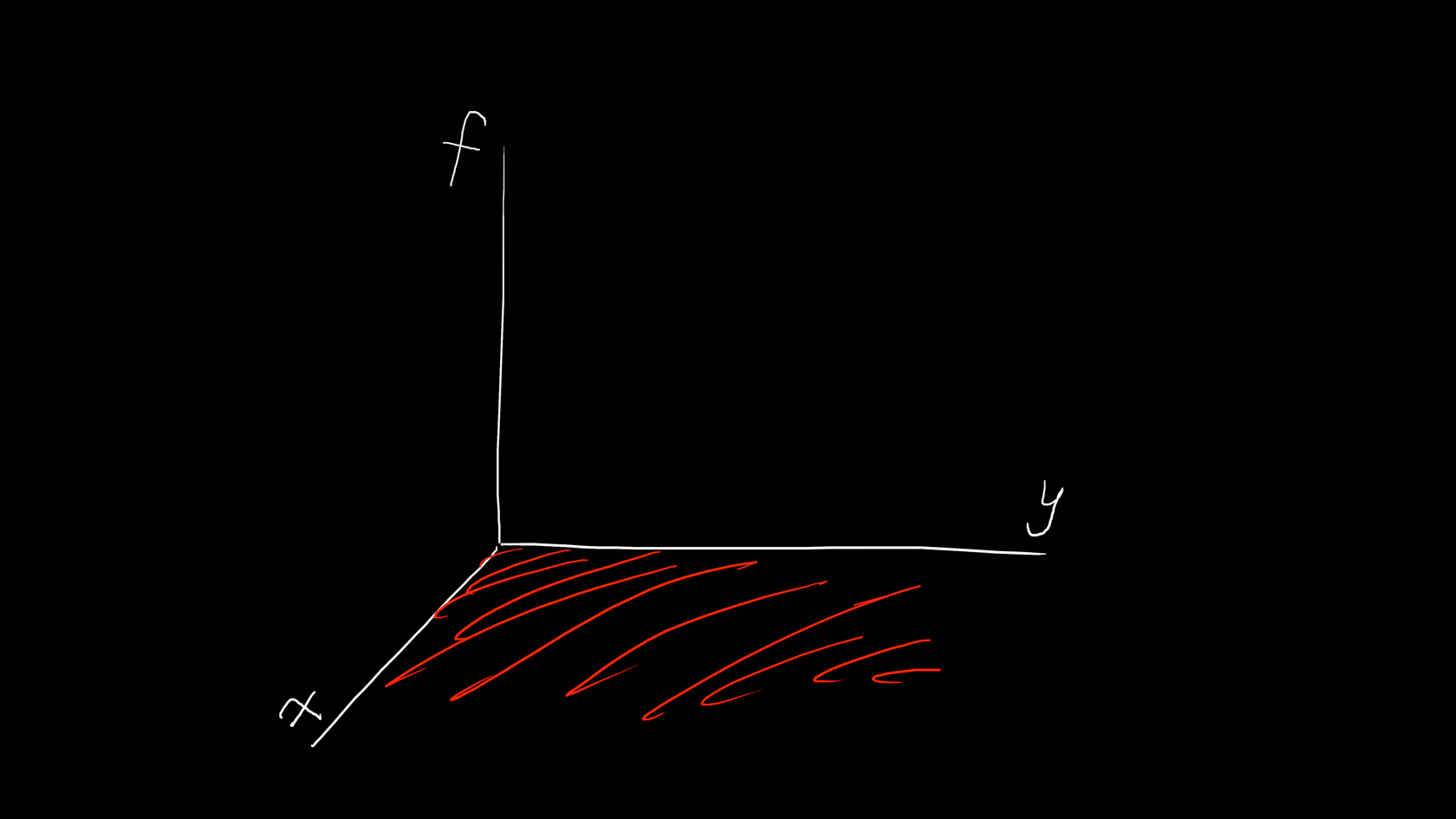


 关于 LearnKu
关于 LearnKu



