行列式

行列式

首先来看个求面积问题：

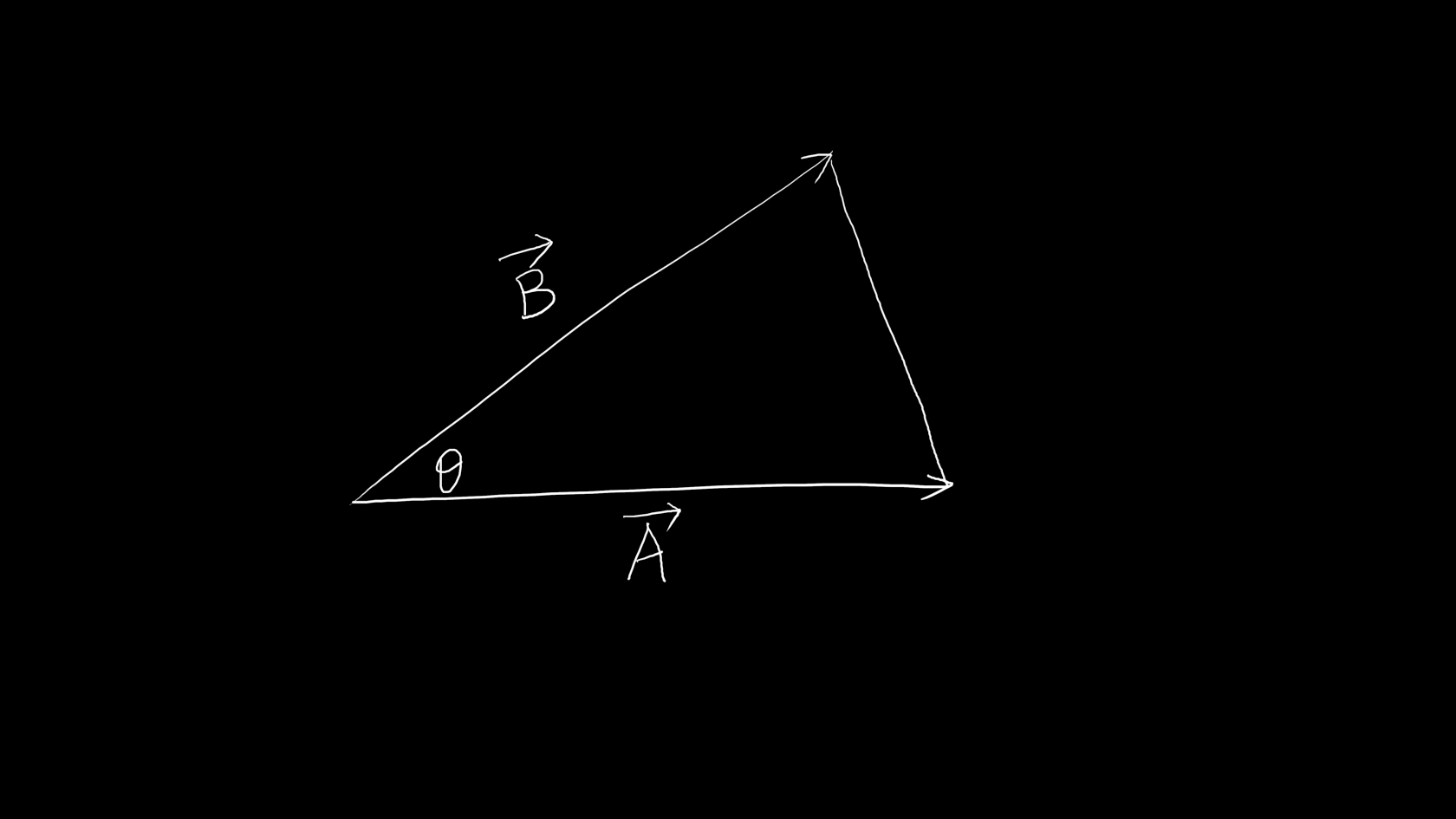
这个三角形面积是\displaystyle\frac{1}{2}|\vec{A}||\vec{B}|\sin\theta，因为三角形的面积是平行四边形的一半。
先通过点乘求\cos\theta，在用\sin^2\theta+\cos^2\theta=1求\sin\theta。
把\vec{A}正方向旋转90\degree得到\vec{A’}：

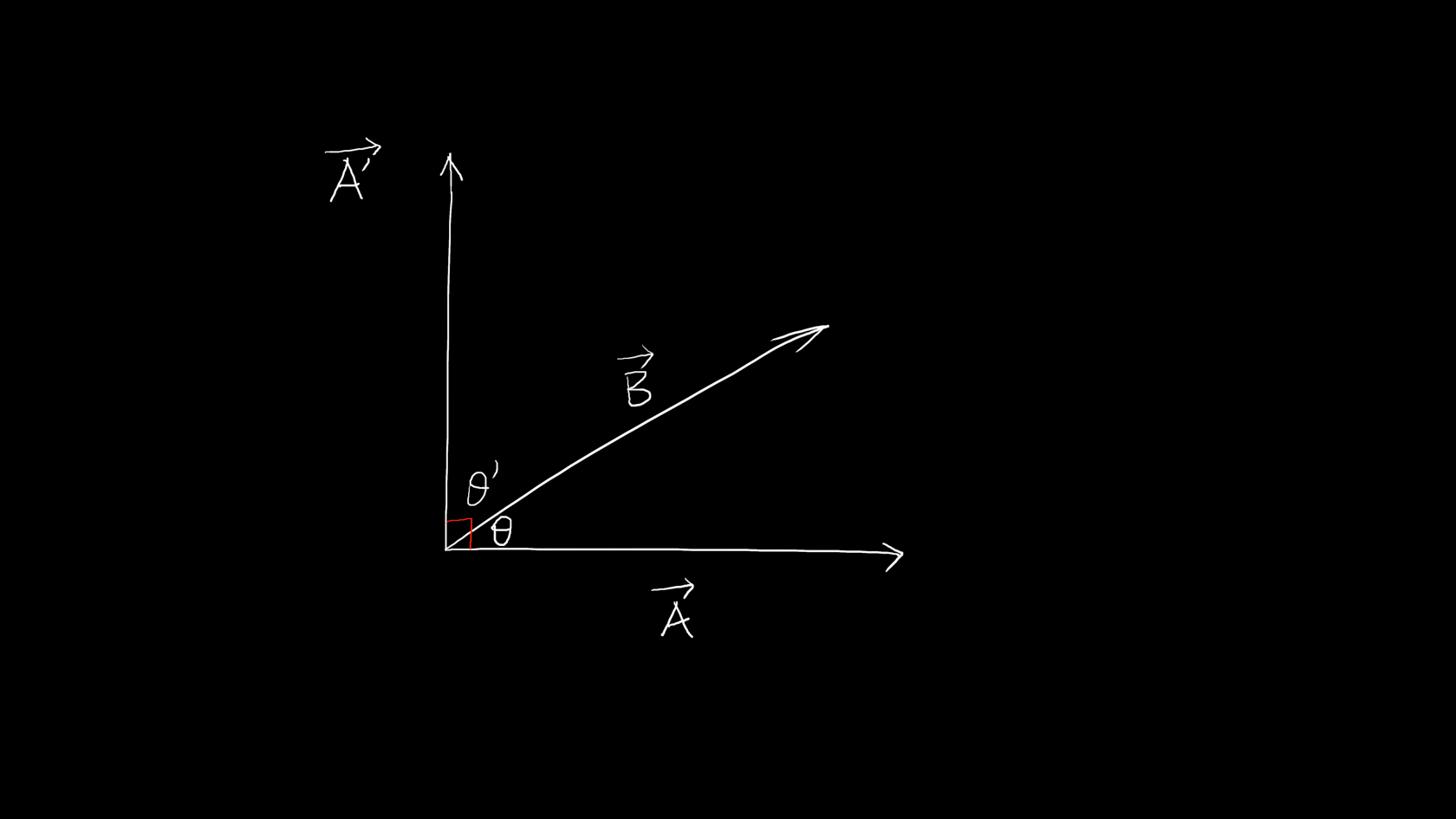
\displaystyle \theta=\frac{\pi}{2}-\theta\\{}\\ \cos(\theta')=\sin\theta

我们知道\vec{A}和\vec{B}两个向量构成的是一个平面，我们所说的旋转90\degree也是在这个平面上旋转，所以\vec{A}=\langle a_1,a_2\rangle,\vec{B}=\langle b_1,b_2\rangle，根据\vec{A}得出\vec{A’}：

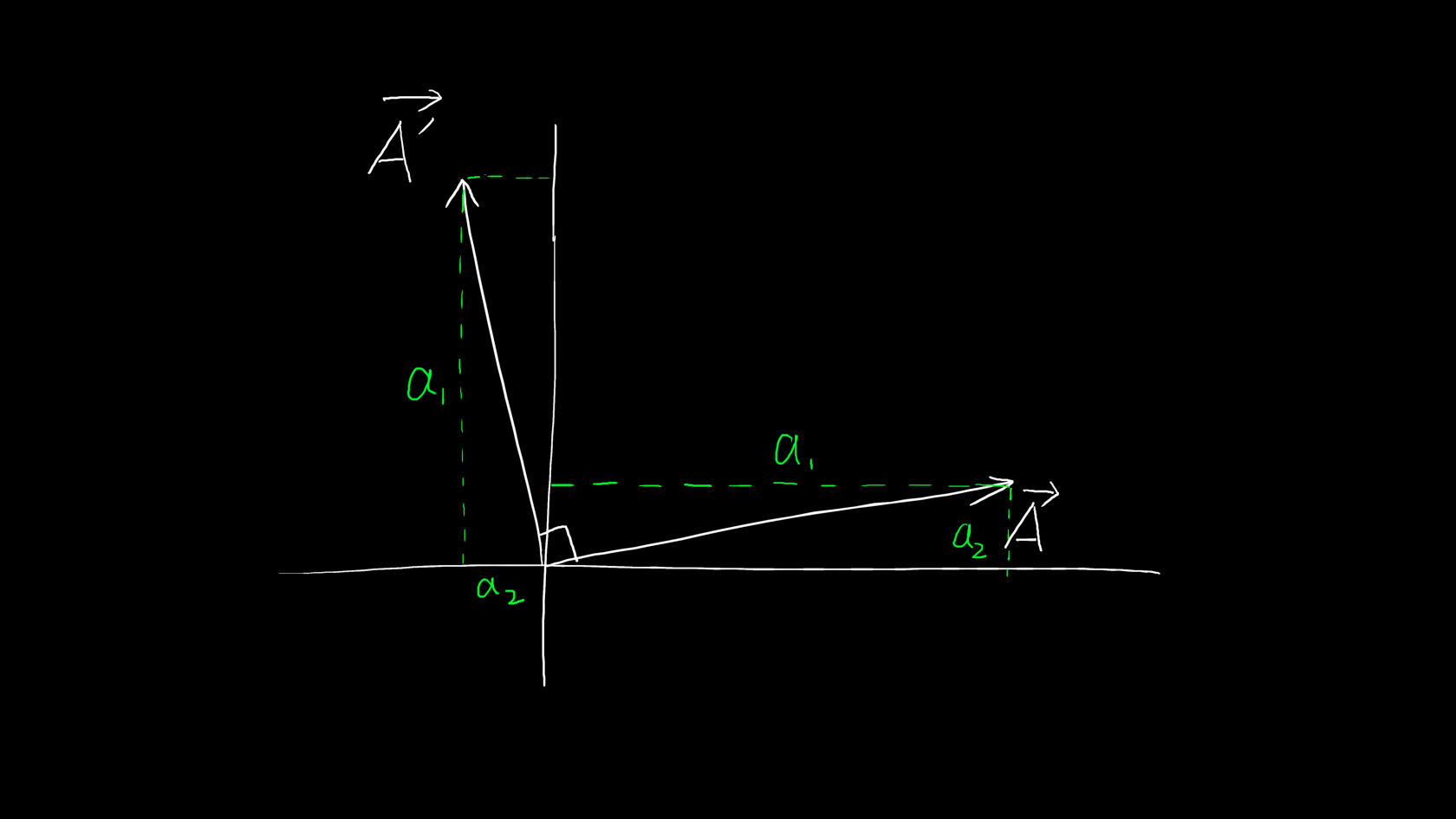
\displaystyle \vec{A'}=\langle-a_2,a_1\rangle\\{}\\ |\vec{A}||\vec{B}|\sin\theta=|\vec{A'}||\vec{B}|\cos(\theta')\\{}\\=\vec{A'}\cdot\vec{B}=\langle-a_2,a_1\rangle\cdot\langle b_1,b_2\rangle=a_1b_2-a_2b_1

以上答案实际上是个行列式，可以用两个向量的行列式表达：

\displaystyle \mathrm{det}(\vec{A},\vec{B})= \left|\begin{array}{c} a_1 & a_2\\ b_1 & b_2 \end{array}\right|

行列式得出来的是一个值，这个2\times2的行列式叫做二阶行列式，它的值是主对角线之积减去次对角线之积，主对角线就是左上角往右下的那条对角线，次对角线就是右上角往左下角的那条对角线。
\mathrm{det}(\vec{A},\vec{B})叫做\vec{A},\vec{B}的行列式。
这个行列式得出的是正负平行四边形的面积：

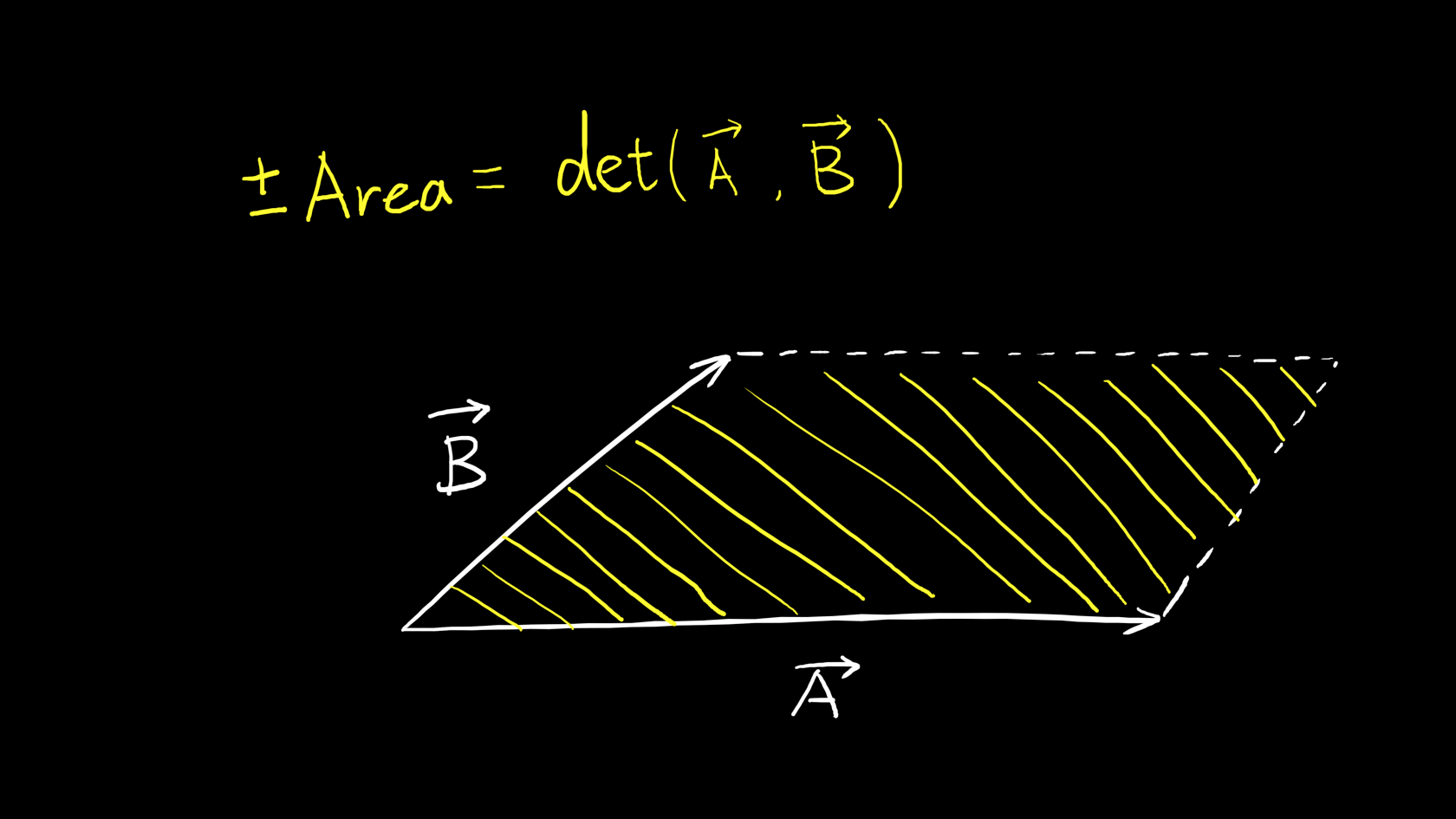
以上我们了解到了两个向量所组成的平行四边形的正负面积等于|\vec{A}||\vec{B}|\sin\theta=\mathrm{det}(\vec{A},\vec{B})。

现在把这个二阶行列式扩展到三阶行列式：

\displaystyle \mathrm{det}(\vec{A},\vec{B},\vec{C})= \left|\begin{array}{c} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 &c_3 \end{array}\right|\\{}\\ =a_1\left|\begin{array}{c} b_2 & b_3\\ c_2 & c_3 \end{array}\right|-a_2\left|\begin{array}{c} b_1 & b_3\\ c_1 & c_3 \end{array}\right|+a_3\left|\begin{array}{c} b_1 & b_2\\ c_1 & c_2 \end{array}\right|

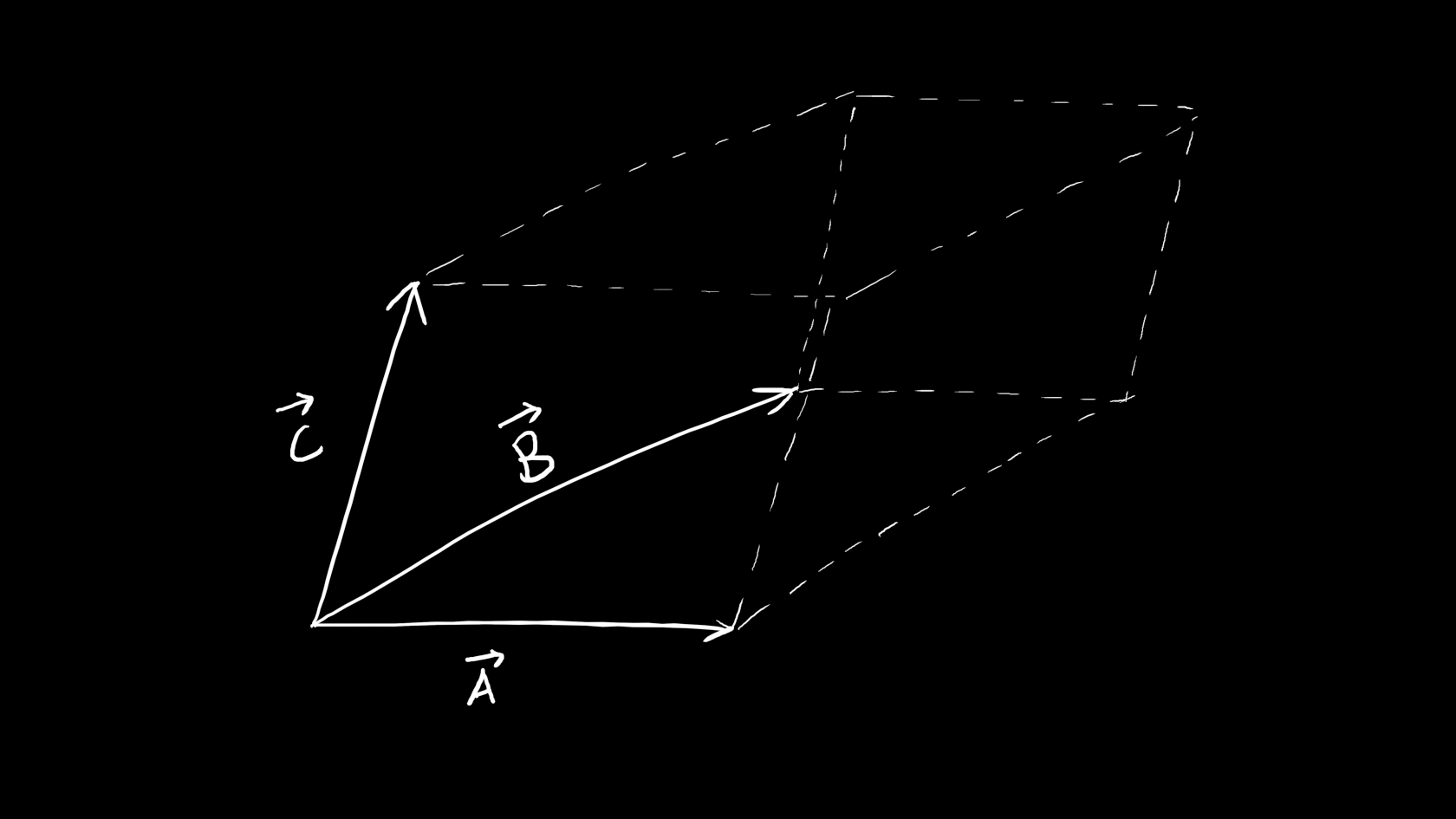
\mathrm{det}(\vec{A},\vec{B},\vec{C})等于\vec{A},\vec{B},\vec{C}所组成的平行六面体的正负体积：