Join 表时数据库是如何选择 Join 的顺序

MySQL

介绍

Dolt 是Git for Data。。它是一个SQL数据库，您可以克隆、分叉、分支和合并。Dolt的SQL引擎是 go-mysql-server，今天我们将讨论它如何实现连接计划，以使涉及多个表的查询计划尽可能高效。

什么是加入计划?

当查询涉及多个表时，有许多不同的方法可以访问这些表以获得正确的结果。但有些方法比其他方法快得多！选择访问表的顺序和组合结果行的策略称为连接规划。这最容易用一个例子来解释。

让我们创建三个表来跟踪城市和州的人口，以及居住在其中的人。如果您已经安装了Dolt (请参阅的说明此处)，您可以按照下面的操作进行操作。
% mkdir join-planning && cd join-planning
% dolt init
Successfully initialized dolt data repository.
% dolt sql

# Welcome to the DoltSQL shell.
# Statements must be terminated with ';'.
# "exit" or "quit" (or Ctrl-D) to exit.
join_planning> create table states (name varchar(100) primary key not null, population int unsigned);
join_planning> create table cities (name varchar(100) primary key not null, state varchar(100) not null, population int unsigned);
join_planning> create table people (name varchar(100) primary key not null, city varchar(100) not null);

假设我们想要一个名为“John Smith”的人的列表，以及他们居住的城市和州的名字和人口。我们可以这样写一个查询:

select * from people p
    join cities c on p.city = c.name
    join states s on s.name = c.state
    where p.name = "John Smith";

查询规划器执行此查询的方法有很多。一种非常糟糕的方法是查看所有三个表中每一行的每个组合，并测试每个组合，看看它是否匹配 JOIN 条件和 WHERE 子句。这是正确和有效的，但非常昂贵。如果我们说 states, cities 和 people 表分别包含 S, C 和 P 行，那么这个查询计划(称为交叉连接)将导致 S * C * P 行访问和比较。这是个坏主意。

你可以使用一些简单的技巧来加快查询的执行速度。使用 pushdown optimization，你可以消除对 people 表的大部分访问。假设数据库中 “约翰·史密斯”的数量称为J，和它比 P小得多。然后智能地使用下推降低了我们访问 S * C * J的成本。

直到几周前，这还只是 Dolt 在连接三个或更多表时所能做到的。对于两个表，如果可用，我们将使用索引。但对于三个人来说，运气不好。它使得产品边界无法用于具有此查询模式和重要数据大小的工作负载。

这篇博文是关于我们如何优化连接计划器，以便为任意数量的表生成更智能、更高效的查询计划。在今天版本的 Dolt中，相同的查询将生成以下查询计划:

join_planning> explain select * from people p
    join cities c on p.city = c.name
    join states s on s.name = c.state
    where p.name = "John Smith";
+-------------------------------------------------------------+
| plan                                                        |
+-------------------------------------------------------------+
| IndexedJoin(p.city = c.name)                                |
|  ├─ Filter(p.name = "John Smith")                           |
|  │   └─ Projected table access on [name city]               |
|  │       └─ TableAlias(p)                                   |
|  │           └─ Indexed table access on index [people.name] |
|  │               └─ Exchange(parallelism=16)                |
|  │                   └─ Table(people)                       |
|  └─ IndexedJoin(s.name = c.state)                           |
|      ├─ TableAlias(c)                                       |
|      │   └─ IndexedTableAccess(cities on [cities.name])     |
|      └─ TableAlias(s)                                       |
|          └─ IndexedTableAccess(states on [states.name])     |
+-------------------------------------------------------------+

该计划首先对people的name列进行索引访问，以查找所有约翰-史密斯。然后，对每一行使用主键索引查找城市。然后，对于每个城市，使用另一个主键查找州。这样，总查询成本为 J * 3。

会很多吗?

用一些真实的数字来说明这一点：我们以美国为例，假设有 330,000,000 条 “人 “行、20,000 条 “城市 “行和 52 条 “州 “行（我们没有忘记华盛顿特区和波多黎各）。交叉连接查询计划访问的行数等于这些数字的乘积，即大约 343 万亿次访问。这是一个很大的数字。你的查询将无法完成。

约有 48,000 人名叫约翰-史密斯在美国。因此，使用 pushdown 优// 如果该表是左连接或右连接的一部分，请确保表的顺序正确。在这种情况下，连接条件中引用的
// 在这种情况下，连接条件中引用的任何表都不能在此表之前。// 如果该表是左连接或右连接的一部分，请确保表的顺序正确。在这种情况下，连接条件中引用的
// 在这种情况下，连接条件中引用的任何表都不能在此表之前。化后，我们的行访问量降到了约 500 亿次。这比以前好多了，但仍然很糟糕。查询没有返回。

另一方面，同时使用对 “人员 “表的下推以及对 “城市 “和 “州 “的索引访问，会将查询的执行限制在对 “人员 “表的访问次数为 48,000 次，然后对 “城市 “和 “州 “表中的每一行各进行一次访问。这就是 3 * 48,000，或总共 144,000 次表访问。

连表计划

访问的行数

交叉连表

343 * 10^12

交叉连接与下推

50 * 10^9

下推和索引访问

144 * 10^3

与 pushdown 博客不同的是，我懒得详细说明节省的百分比。第一次优化会带来小数点后 4 个数量级的改进，第二次优化又会带来 5 个数量级的改进。这就是 Dolt 是一个可用的查询引擎还是一个糟糕的空间加热器的区别。

它是如何运作的？

要组装一个高效的查询计划，首先必须回答一个非常重要的问题：

我们应该以什么顺序访问表？

这确实会带来很大的不同。在上面的示例中，”人 > 城市 > 州 “的表访问顺序让我们可以使用后两个表的主键索引。如果我们选择的顺序是 “州 > 城市 > 人”，我们就不能使用前面表中的信息来减少后面表中的查找次数，从而导致交叉连接。

有很多有趣的细节会出错，但要正确处理表的顺序，可以使用一些非常简单的启发式方法。

我可以使用什么索引来访问这个表？这些列是连接条件的一部分吗？
是否有必要的列可用作键？连接条件中的其他表是否在此表之前？
如果需要进行全表扫描，此表中有多少行？
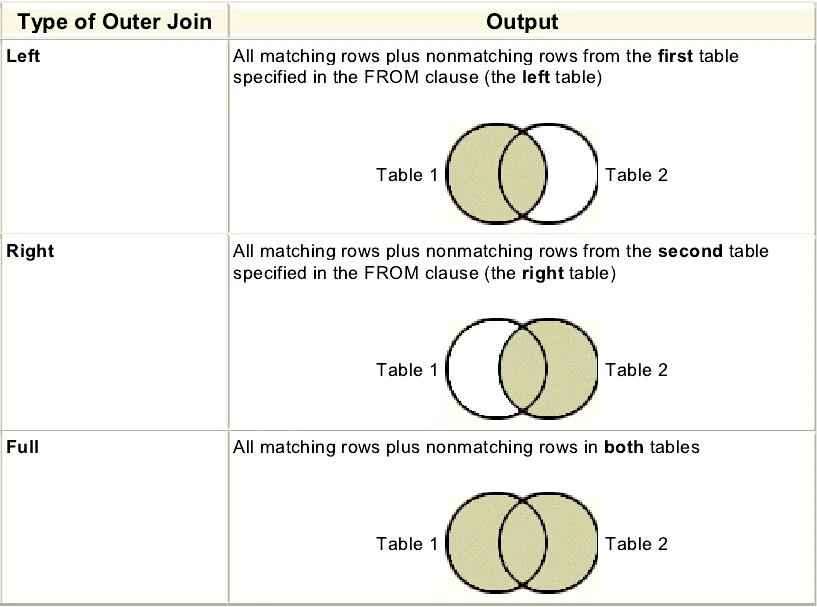
这是 “左 “连接还是 “右 “连接？

我们稍后再来看表排序算法的实际实现。现在，让我们假设它的存在，它告诉我们访问表的顺序。我们如何根据访问顺序构建连接计划呢？

连接计划不是同构的

在 go-mysql-server 中，查询计划是以 Node 对象的树形结构组织的。目前，所有节点都最多有两个子节点，因此查询计划是一棵二叉树。一个 Join 节点知道如何从其左侧子节点获取一条记录，然后遍历其右侧子节点，寻找与连接条件匹配的记录。当右侧子节点的迭代器中没有记录时，它会从左侧子节点获取下一条记录。最终，左侧子代中的行将用完，迭代器将返回 io.EOF 。

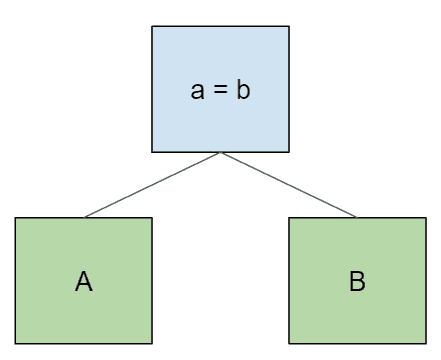
像其他任何事情一样，通过一些示例最容易直观地理解这一点。在所有这些示例中，我们将使用单字母表名和与表名匹配的单列。下面是两个表 A 和 B 之间的简单连接：

select * from A join B on a = b;

一个简单的查询计划是这样的

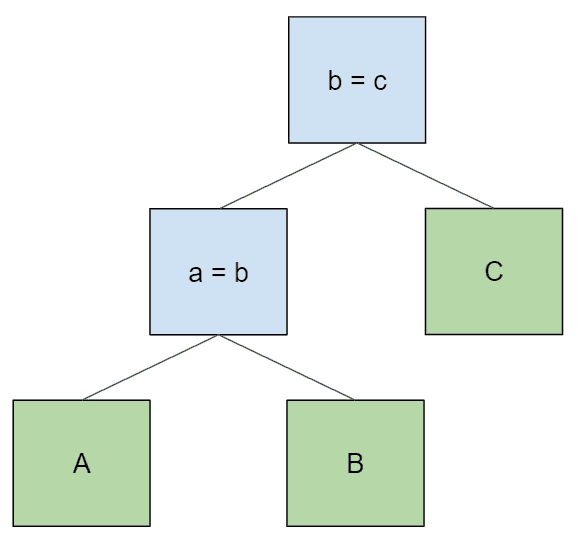
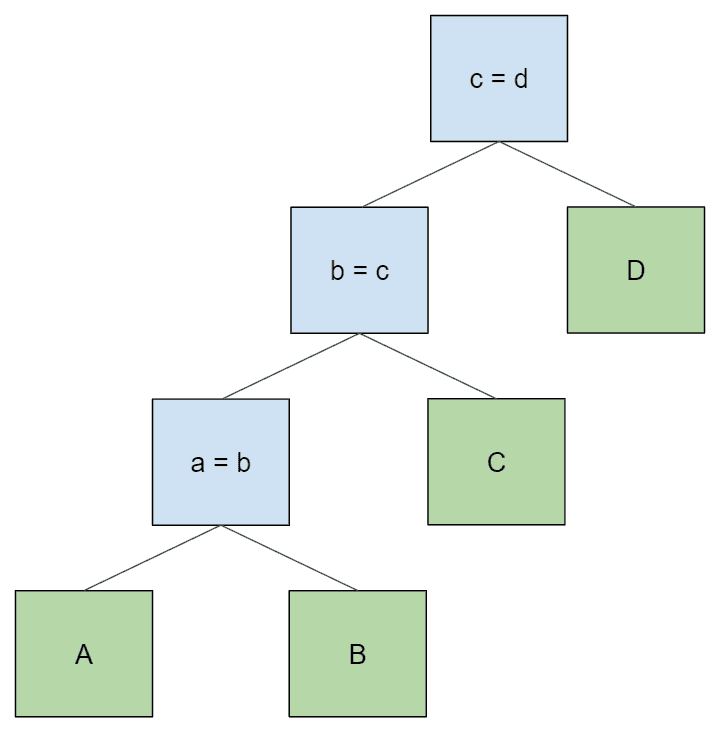
当我们向连接中添加其他表时，这些表就会成为树的新根，而原来的子树则是左侧的子树。

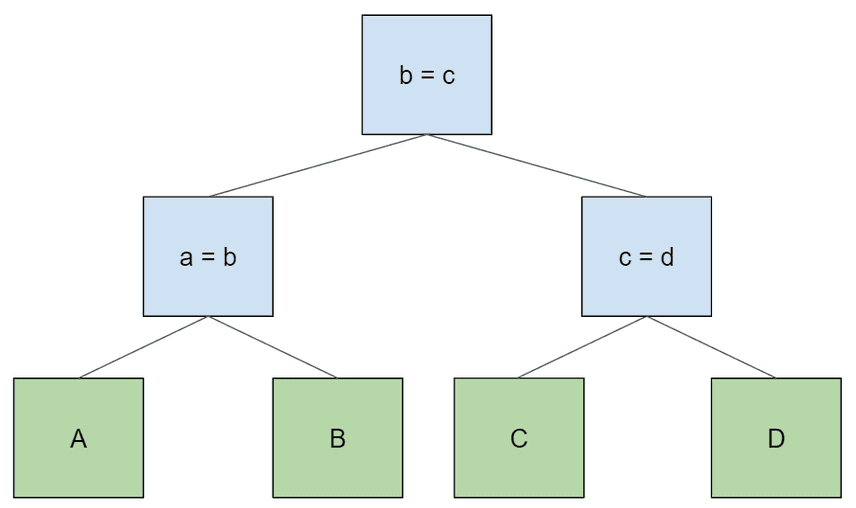
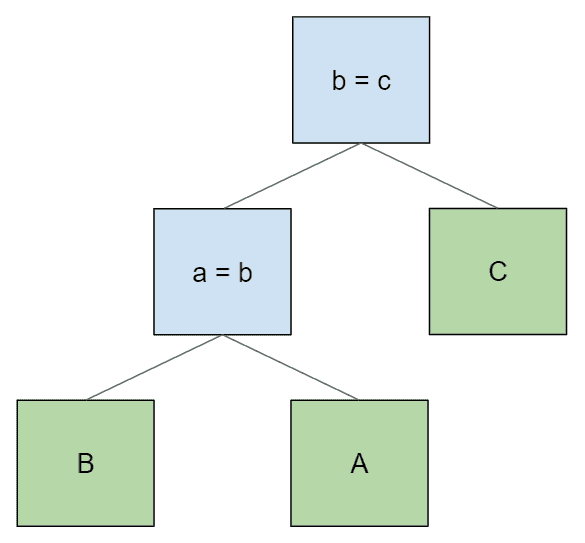
select * from A join B on a = b join C on b = c;

select * from A join B on a = b join C on b = c join D on c = d;

让我们仔细研究一下最后一个例子。当我们在查询的根节点上打开一个迭代器时，会发生什么？它会在它的左侧子节点上打开一个迭代器，这个迭代器又会在它的左侧子节点上打开一个迭代器，依此类推。每个节点从其左侧子节点访问一条记录后，都会尝试从其右侧子节点查找匹配的记录。最终，表的访问顺序与词法查询相同： a > b > c > d`。

让我们跟踪一下结果集中单行的执行情况。

连接节点 a = b 从 A 中获取一条记录。然后遍历 B 中的记录，查找与连接条件 a = b 匹配的记录。当找到这样一条记录时，就会返回它。
节点 b = c 从它的左子节点获取记录，该子节点是表 A 和表 B 中记录的连接。然后遍历其右侧子节点，即 C 表中的记录，查找与连接条件 b = c 匹配的记录。当找到这样的行时，它将返回该行。
节点 c = d 从它的左侧子节点中获取一条记录，它是 A、B 和 C 中的记录的连接，顺序为 A、B 和 C 。然后，它试图匹配其右侧子节点 D 中的行，如上所述。

重要的是，有时有许多可能的二叉树可以实现上述逻辑，从而为任何给定的表访问顺序产生正确的结果。在上面的树构造算法中，我们不断将子树向下推移到新连接节点的左侧子节点，这只是解析器默认给出的结果，因为它是左关联的。但我们还可以画出其他结果相同的树。例如，下面是一棵平衡连接树：

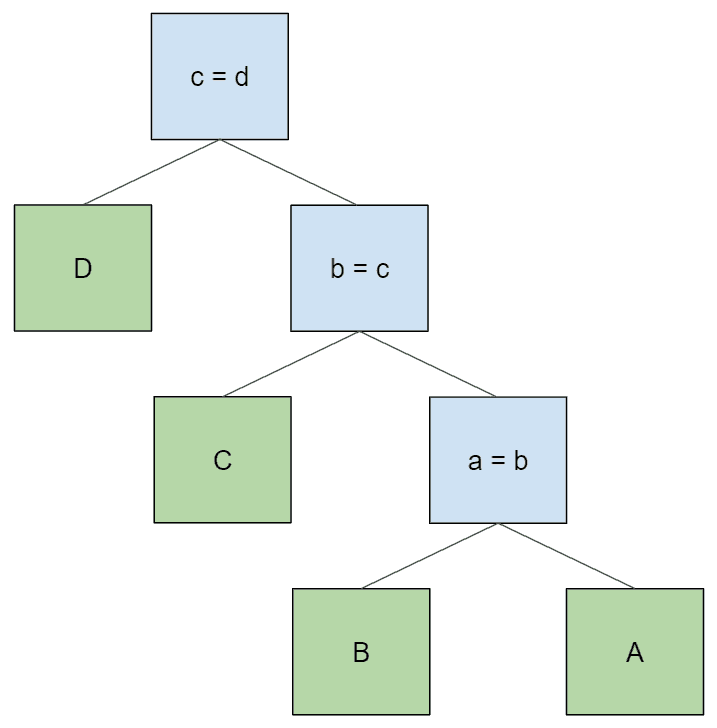
与原始树一样，这样产生的表格访问顺序为 “A > B > C > D”。如果我们想以相反的顺序访问表，可以像这样简单地翻转原始树中每个节点的左右子节点：

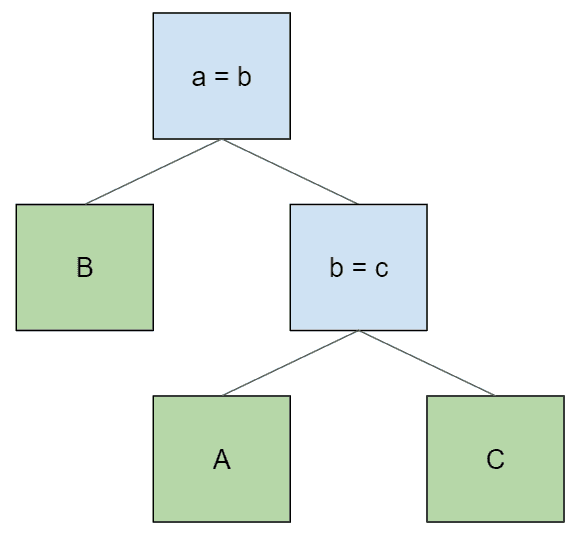
同样，对于给定的表排序，有时会有许多可能的连接树。但它们都有一个共同点：它们的连接条件都指向可以在其左右子节点中找到的表。否则，节点无法评估其连接条件。例如，假设我们正在查询三个表，并希望按照 “B > A > C “的顺序访问它们。在这种表排序下，这是一个无效的连接计划：

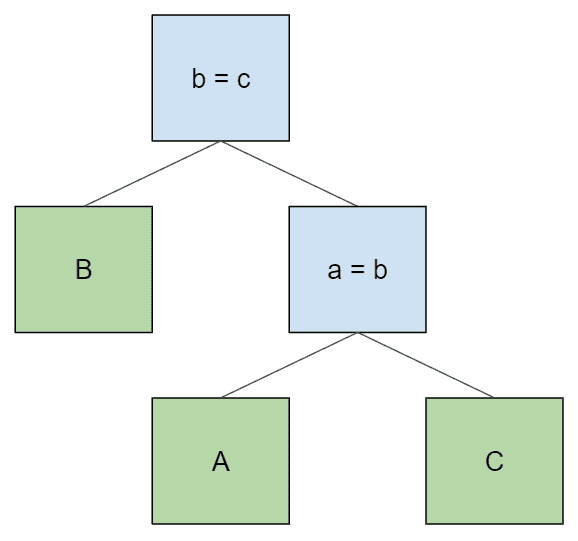
这个计划无效，因为节点 b = c 没有表 B 作为后代，所以无法评估其连接条件。我们也不能通过交换连接条件来解决这个问题：

下层连接条件仍未满足，这次是因为它需要表 B，而表 B 没有作为它的后代。为了得到 “B > A > C “的顺序并满足连接条件，我们需要生成这棵树：

连接搜索

我们可以利用上述关于构建连接树的见解，提出一种构建连接树的通用算法。这是一个约束求解/搜索问题，在源代码中，我称之为连接搜索。

从一组可用的连接条件中 选择一个连接条件。
使用剩余的表和连接条件，递归地为该连接条件构建所有可能的左子树。
检查每个可能的左子树是否有效：表必须按顺序排列，连接条件必须满足。如果子树无效，则放弃该子树，检查下一个子树。
使用剩余的表和连接条件，递归 构建该连接条件下所有可能的右子树（确保删除左子树使用的所有表和连接条件）。再次放弃无效的子树。
如果找不到有效的左子树或右子树，就放弃，回到第一步，重新选择一个新的连接条件。

与本技术博客系列中的大多数内容一样，这个想法相对简单，但有许多小细节会搞砸。由于 “节点 “对象操作起来非常麻烦，因此我创建了一种简化类型来表示搜索过程中的连接树：

// joinSearchNode 是一种简化类型，代表一个连接树节点，它既可以是一个内部节点（连接），也可以是一个
// 叶节点（表）。连接树的顶层节点总是内部节点。每个内部节点都有一个
// 左子节点和右子节点。
type joinSearchNode struct {
    table string // 如果是内部节点则为空
    joinCond *joinCond // 如果是叶节点，则为 nil
    parent *joinSearchNode // 如果是根节点则为 nil
    left *joinSearchNode // 如果是叶节点，则为 nil
    right *joinSearchNode // 如果是叶节点，则为 nil
    params *joinSearchParams // 组装此节点的搜索参数
}

除了正常的树形结构外，这种类型还跟踪父指针（以便更容易从根走到验证表排序规则）和搜索参数，以跟踪哪些表和连接条件可供使用。

下面是实现这种算法的 searchJoins 函数的一部分。完整代码链接在上面。

func searchJoins(parent *joinSearchNode, params *joinSearchParams) []*joinSearchNode {
    // 我们的目标是为给定的父节点构建所有可能的子节点。
    //合法子树的每一种排列都应进入这个列表。
    children := make([]*joinSearchNode, 0)

    // <snipped code appending tables to the list of children>

    for i, cond := range params.joinConds {
        if params.joinCondIndexUsed(i) {
            continue
        }

        paramsCopy := params.copy()
        paramsCopy.usedJoinCondsIndexes = append(paramsCopy.usedJoinCondsIndexes, i)

        candidate := &joinSearchNode{
            joinCond: cond,
            parent:   parent,
            params:   paramsCopy,
        }

        // 为每个左分支和右分支找到所有可能的子树，并将所有有效子树添加到列表中
        candidate = candidate.targetLeft()
        leftChildren := searchJoins(candidate, paramsCopy)

        // 注意此区块中的变量阴影
        for _, left := range leftChildren {
            if !isValidJoinSubTree(left) {
                continue
            }
            candidate := candidate.withChild(left).targetRight()
            candidate.params = candidate.accumulateAllUsed()
            rightChildren := searchJoins(candidate, paramsCopy)
            for _, right := range rightChildren {
                if !isValidJoinSubTree(right) {
                    continue
                }
                candidate := candidate.withChild(right)
                if isValidJoinSubTree(candidate) {
                    children = append(children, candidate)
                }
            }
        }
    }

    return children
}

通过管道获取键信息

现在我们有了表顺序和实现该顺序的连接计划，我们需要一种方法来获取计划中后面表的关键信息。我们之所以对表进行排序，是为了在除第一张表之外的每一张表上使用索引查找。对于这些表中的每一张表，我们都希望在连接中传递来自前面所有表的记录的并集，以便使用这些信息为索引构建查找键。

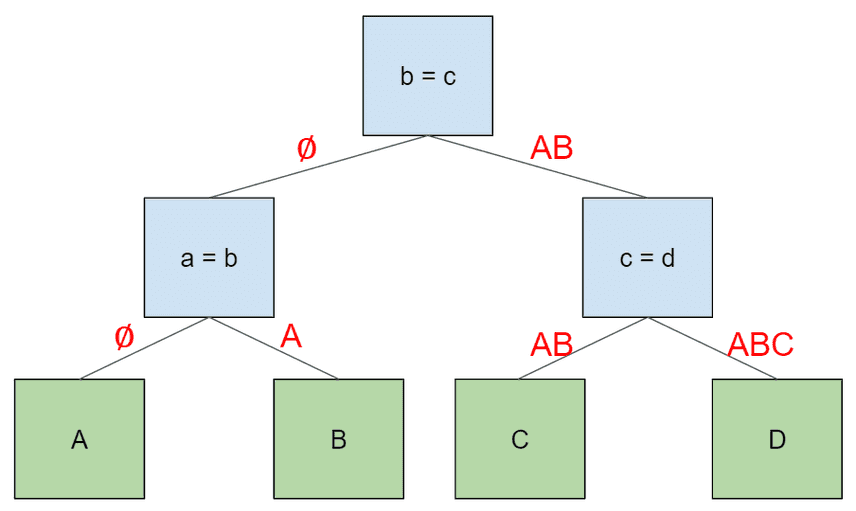
考虑一下这个四表连接计划。对于树中的每条边，我们都会在边上标注子节点需要访问的表，以便在其左边的表中查找键信息。

每个连接节点将向其左侧子节点提供它收到的记录（根节点为空）。然后，它将向其右侧子节点提供该行与左侧子节点所接收行的连接。这相当于在树上按顺序行走，按照我们在开始时指定的顺序访问表。首先，根节点以空行向左遍历。同样的情况也发生在第一个子节点（a = b）上。当这个子节点向右遍历时，它会提供其左侧子节点 A 的行。然后根节点向右遍历，并提供其左侧子节点的行，即与 AB 相对应的行。同样的情况也发生在最后一个节点 (c=d)，最后一个右侧子节点获得了由其父节点 (AB)和其左侧子节点 (C)连接而成的一行。

与引擎分析的其他大部分工作不同，我们无法自下而上地完成树的转换。从根本上说，这是一种无序行走，因此我们必须使用自定义函数自上而下地完成。下面是其中有趣的部分（做了一些小修改，如删除错误处理模板和简化返回类型）。

func replaceTableAccessWithIndexedAccess(
    node sql.Node,
    schema sql.Schema,
    scope *Scope,
    joinIndexes joinIndexesByTable,
    exprAliases ExprAliases,
    tableAliases TableAliases,
) sql.Node {

    switch node := node.(type) {
    case *plan.TableAlias, *plan.ResolvedTable:
        // 如果可用模式可以在该表上建立索引，则使用该索引，用索引访问替换该表
        indexes := joinIndexes[node.(sql.Nameable).Name()]
        indexToApply := indexes.getUsableIndex(schema)
        if indexToApply == nil {
            return node
        }

        node, err := plan.TransformUp(node, func(node sql.Node) (sql.Node, error) {
            switch node := node.(type) {
            case *plan.ResolvedTable:
                if _, ok := node.Table.(sql.IndexAddressableTable); !ok {
                    return node
                }

                keyExprs := createIndexLookupKeyExpression(indexToApply, exprAliases, tableAliases)
                keyExprs, err := FixFieldIndexesOnExpressions(scope, schema, keyExprs...)

                return plan.NewIndexedTableAccess(node, indexToApply.index, keyExprs)
            default:
                return node
            }
        })

        return node
    case *plan.IndexedJoin:
        // 使用输入模式从左侧向下递归
        left, replacedLeft, err := replaceTableAccessWithIndexedAccess(node.Left(), schema, scope, joinIndexes, exprAliases, tableAliases)

       // 然后在右侧添加左侧的模式
       right, replacedRight, err := replaceTableAccessWithIndexedAccess(node.Right(), append(schema, left.Schema()...), scope, joinIndexes, exprAliases, tableAliases)

       // 如果表格顺序发生变化，可能需要调整条件的字段索引
       cond, err := FixFieldIndexes(scope, append(schema, append(left.Schema(), right.Schema()...)...), node.Cond)
       return plan.NewIndexedJoin(left, right, node.JoinType(), cond)
   default:
       // 其他节点类型
       newChild, replaced, err := replaceTableAccessWithIndexedAccess(node.Child, schema, scope, joinIndexes, exprAliases, tableAliases)
       return node.WithChildren(newChild)
   }
}

回到起点：选择表格顺序

现在我们又回到了起点：如何决定访问表的顺序？这部分相对容易，因为我们已经将所有其他部分整合在一起了。要确定最佳顺序，我们只需要一组附带索引信息的连接条件。这样，函数的编写就非常简单了：

// orderTables 返回所提供表格的访问顺序，试图将总查询成本降至最低
func orderTables(tables []NameableNode, tablesByName map[string]NameableNode, joinIndexes joinIndexesByTable) []string {
    tableNames := make([]string, len(tablesByName))
    indexes := make([]int, len(tablesByName))
    for i, table := range tables {
        tableNames[i] = strings.ToLower(table.Name())
        indexes[i] = i
    }

    // 生成表顺序的所有排列
    accessOrders := permutations(indexes)
    lowestCost := int64(math.MaxInt64)
    lowestCostIdx := 0
    for i, accessOrder := range accessOrders {
        cost := estimateTableOrderCost(tableNames, tablesByName, accessOrder, joinIndexes, lowestCost)
        if cost < lowestCost {
            lowestCost = cost
            lowestCostIdx = i
        }
    }

    cheapestOrder := make([]string, len(tableNames))
    for i, j := range accessOrders[lowestCostIdx] {
        cheapestOrder[i] = tableNames[j]
    }

    return cheapestOrder
}

但这有点掩耳盗铃。估算查询成本才是重点。

// 估计所给表格排序的成本。数字越小越好。如果成本超过目前发现的最低值就返还
// 如果我们有表格和键的统计信息，我们可以做得更好。
func estimateTableOrderCost(
    tables []string,
    tableNodes map[string]NameableNode,
    accessOrder []int,
    joinIndexes joinIndexesByTable,
    lowestCost int64,
) int64 {
    cost := int64(1)
    var availableSchemaForKeys sql.Schema
    for i, idx := range accessOrder {
        if cost >= lowestCost {
            return cost
        }

        table := tables[idx]
        availableSchemaForKeys = append(availableSchemaForKeys, tableNodes[table].Schema()...)
        indexes := joinIndexes[table]

        // 如果该表是左连接或右连接的一部分，请确保表的顺序正确。在这种情况下，连接条件中引用的
        // 在这种情况下，连接条件中引用的任何表都不能在此表之前。
        for _, idx := range indexes {
            if (idx.joinType == plan.JoinTypeLeft && idx.joinPosition == plan.JoinTypeLeft) ||
                (idx.joinType == plan.JoinTypeRight && idx.joinPosition == plan.JoinTypeRight) {
                for j := 0; j < i; j++ {
                    otherTable := tables[accessOrder[j]]
                    if colsIncludeTable(idx.comparandCols, otherTable) {
                        return math.MaxInt64
                    }
                }
            }
        }

        if i == 0 || indexes.getUsableIndex(availableSchemaForKeys) == nil {
            // TODO：估算表格中的行数
            cost *= 1000
        } else {
            // TODO: 根据索引查找结果估算行数。
            cardinality
            cost += 1
        }
    }

    return cost
}

引擎还没有表统计信息，因此我们暂时将任何全表扫描视为 1000 倍，将任何索引查找视为恒定成本。我们还排除了在 “LEFT “或 “RIGHT “连接中错误访问主表的连接计划，使其达到最大成本。

今后的工作

到目前为止，我们主要讨论了表排序和索引查找的使用。这是连接规划的一个重要方面，但不是唯一的方面。除了简单的嵌套循环连接，我们还需要考虑不同的连接策略，例如 SQL Server 广泛使用的哈希连接。对于某些特定大小的表，在内存中加载表结果集并将其与查询的其余部分进行散列连接要比对其进行 N 次索引查找快得多。但这是后话了。

结论

自从我们宣布支持两张表的索引连接以来，已经过去快一年了。从那时起，我们走过了漫长的道路，重写了引擎的大部分内容并添加了大量功能。最新的改进是支持任意数量表的索引连接，这是我为引擎添加的最困难的功能。这需要大量的深思熟虑和分析，大量的实验和错误的开始，以及大量的测试。

但这也是我做过的最令人满意的新增功能。它让查询引擎的速度从异常缓慢变成了对许多客户来说真正实用。它让产品看起来像一个真正的数据库，而不仅仅是一个很酷的玩具。而且，与我几乎所有的专业软件经验不同的是，它真正利用了我在计算机科学教育中所学到的艰深知识。这种感觉真不错。

Dolt是一个学习如何使用 SQL的好工具，现在它在查询三个或更多表时的性能并不可怕。今天就来安装 Dolt试试吧。如果您还没准备好下载该工具，或者只是想提问，请访问与我们在 Discord 上聊天。我们随时欢迎新客户的到来！

本文中的所有译文仅用于学习和交流目的，转载请务必注明文章译者、出处、和本文链接
我们的翻译工作遵照 CC 协议，如果我们的工作有侵犯到您的权益，请及时联系我们。

原文地址：https://www.dolthub.com/blog/2020-12-28-...

译文地址：https://learnku.com/mysql/t/84909

Join 表时数据库是如何选择 Join 的顺序

介绍

什么是加入计划?

会很多吗?

它是如何运作的？

连接计划不是同构的

连接搜索

通过管道获取键信息

回到起点：选择表格顺序

今后的工作

结论

推荐文章：

社区赞助商

关于 LearnKu

资源推荐

服务提供商

其他信息

Join 表时数据库是如何选择 Join 的顺序

介绍

什么是加入计划?

会很多吗?

它是如何运作的？

连接计划不是同构的

连接搜索

通过管道获取键信息

回到起点：选择表格顺序

今后的工作

结论

推荐文章：

社区赞助商

关于 LearnKu

资源推荐

服务提供商

其他信息

请登录