数组#

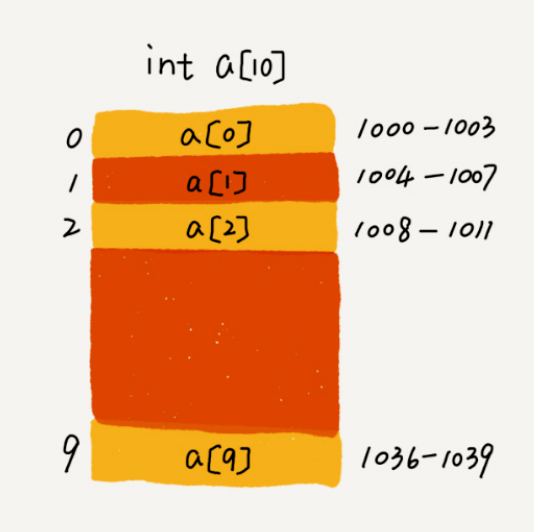
数组（Array）是一种线性表数据结构，它用一组连续的内存空间，来存储一组具有相同类型的数据。PHP 这种动态语言中，因为数组底层是通过散列表实现的，所以功能异常强大，这段常规的数组定义在 PHP 中并不成立，PHP 的数组可以存储任何类型数据，如果与 Java 对比的话，PHP 数组集成了 Java 的数组、List、Set、Map 于一身，所以写代码的效率比 Java 高了几个量级。

链表#

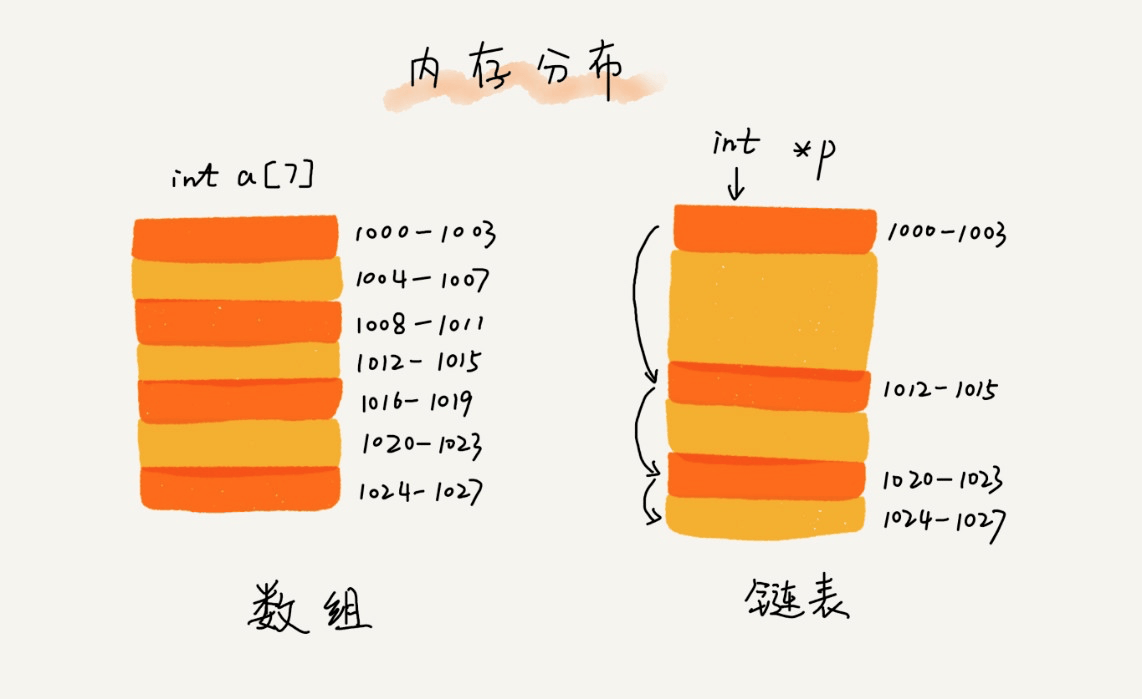
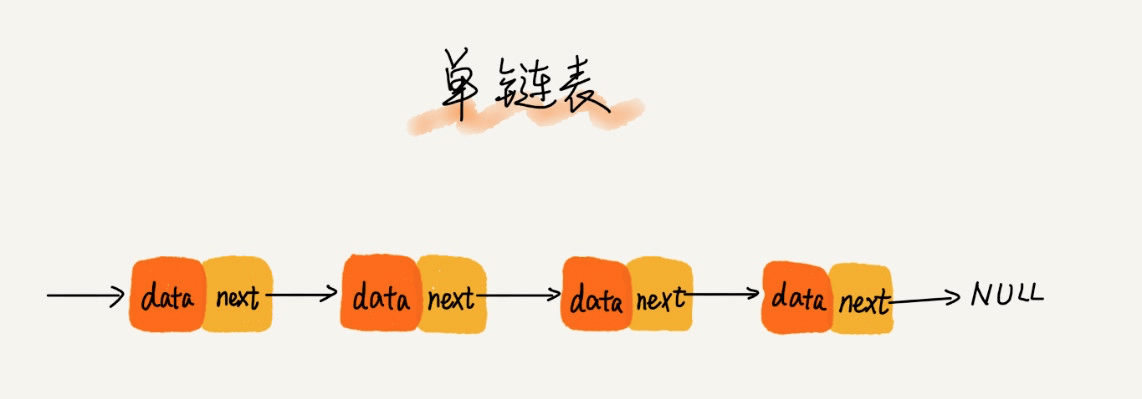
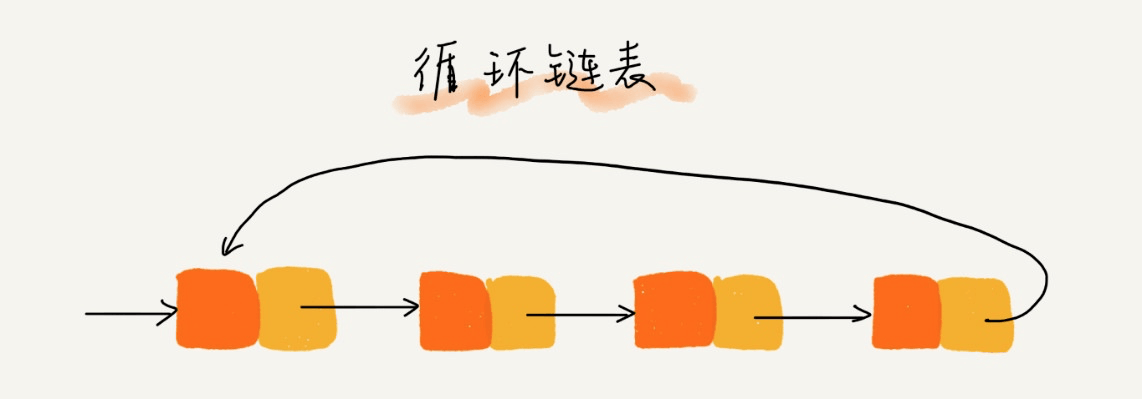
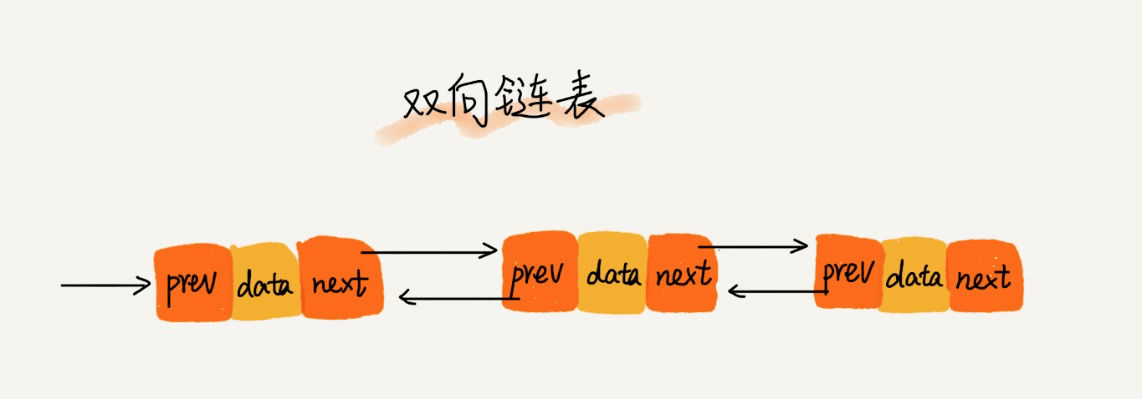
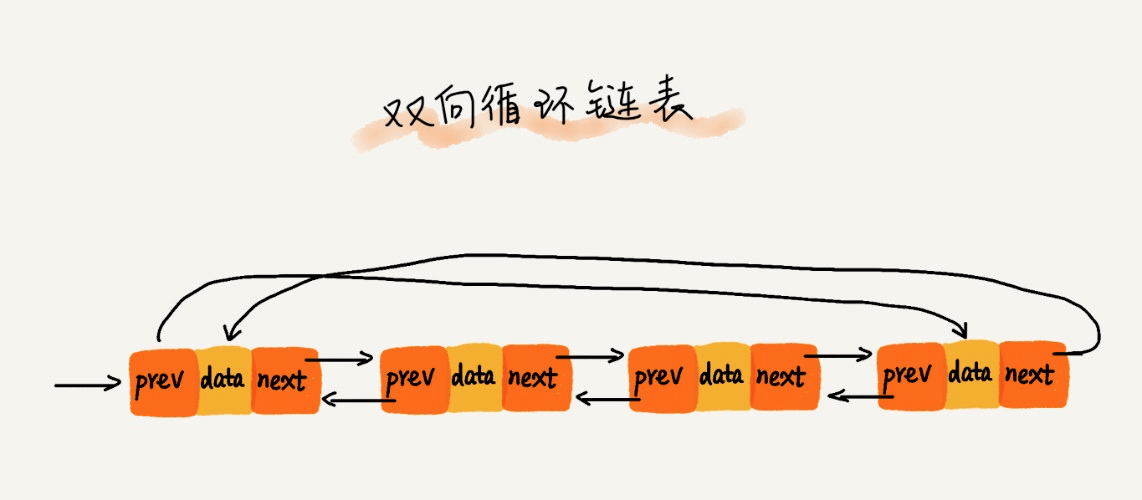
栈#

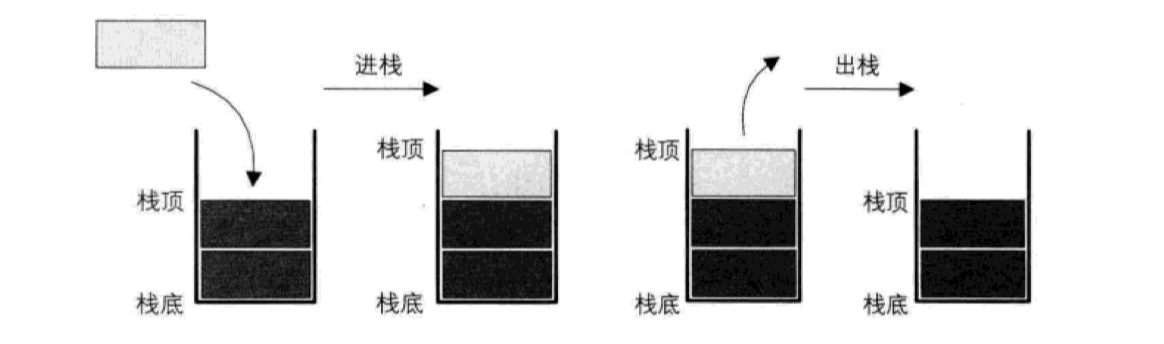
应用：浏览器前进、倒退功能，编辑器 / IDE 中的撤销、取消撤销功能，程序代码中的函数调用、递归、四则运算等等，都是基于堆栈这种数据结构来实现的

队列#

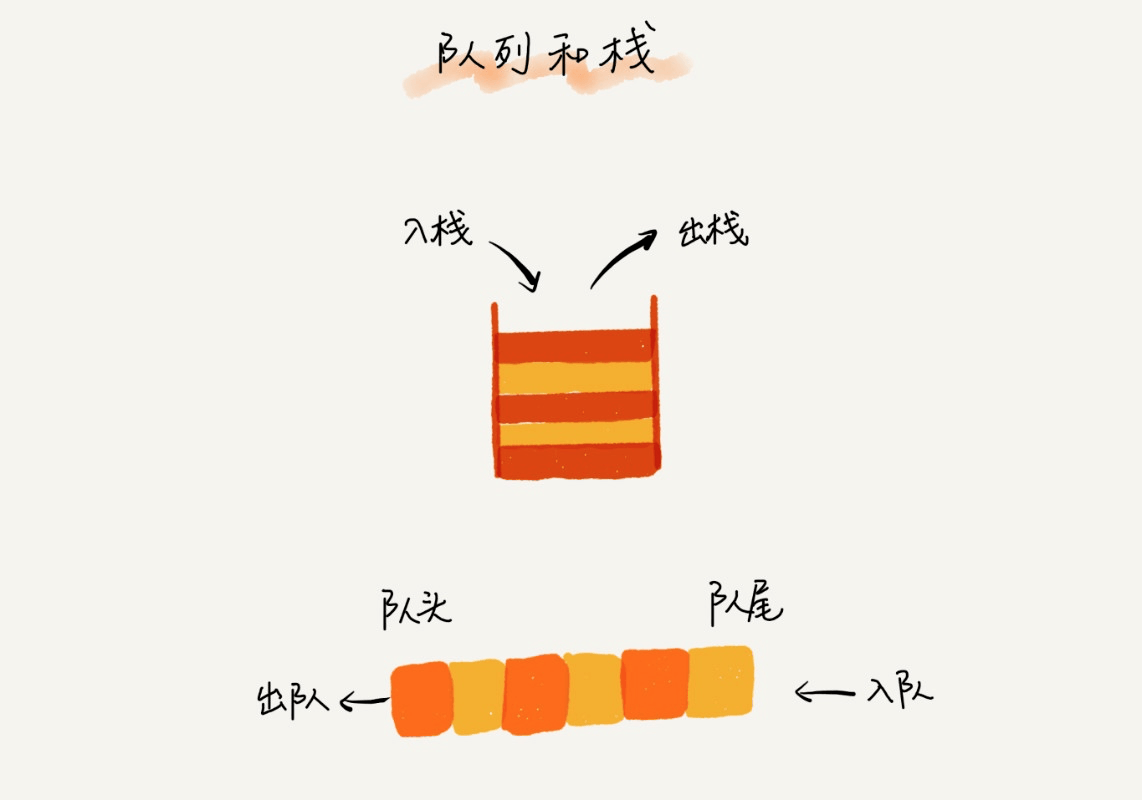
应用：消息队列就是队列的典型应用场景

冒泡排序#

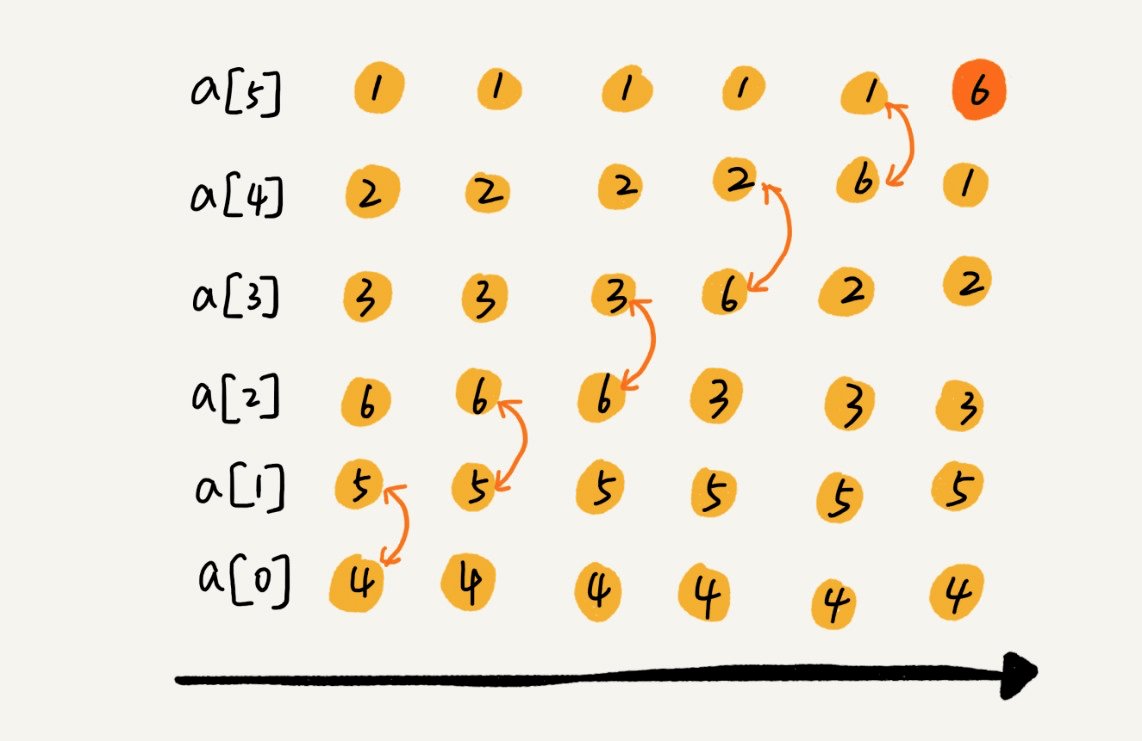
插入排序#

选择排序#

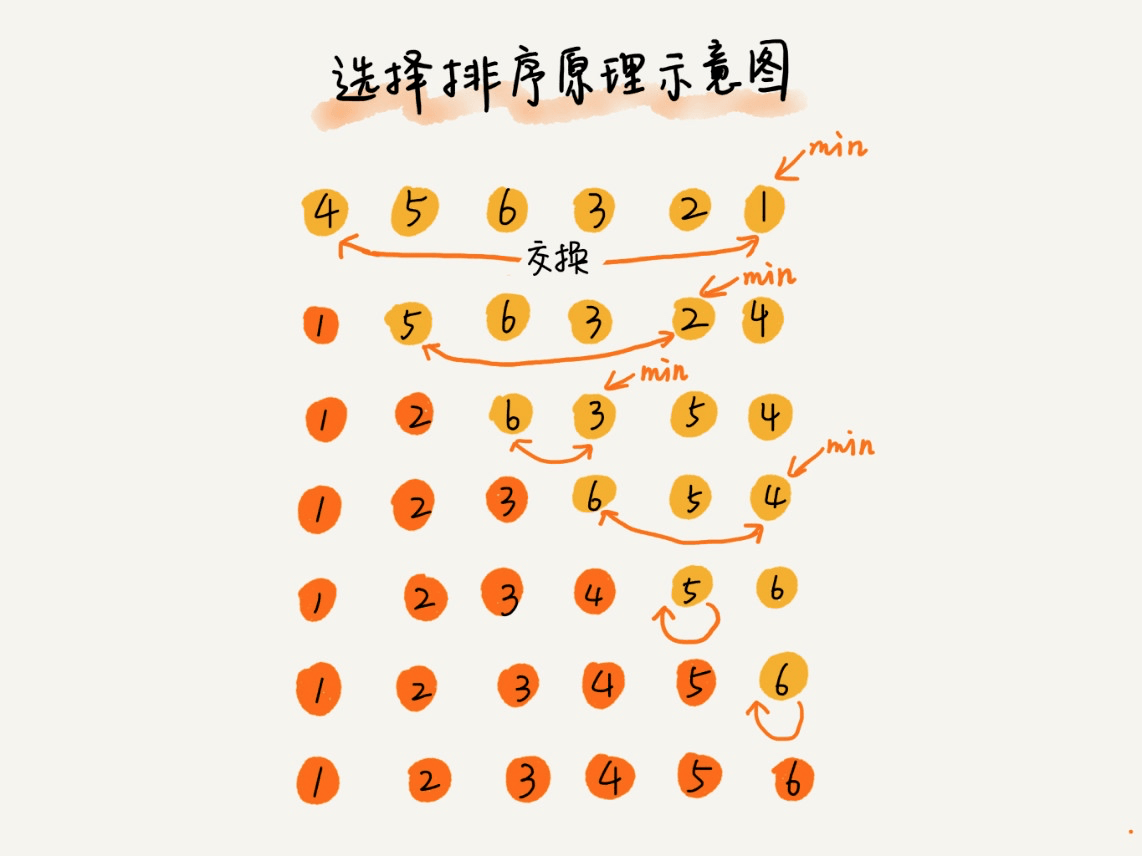
归并排序#

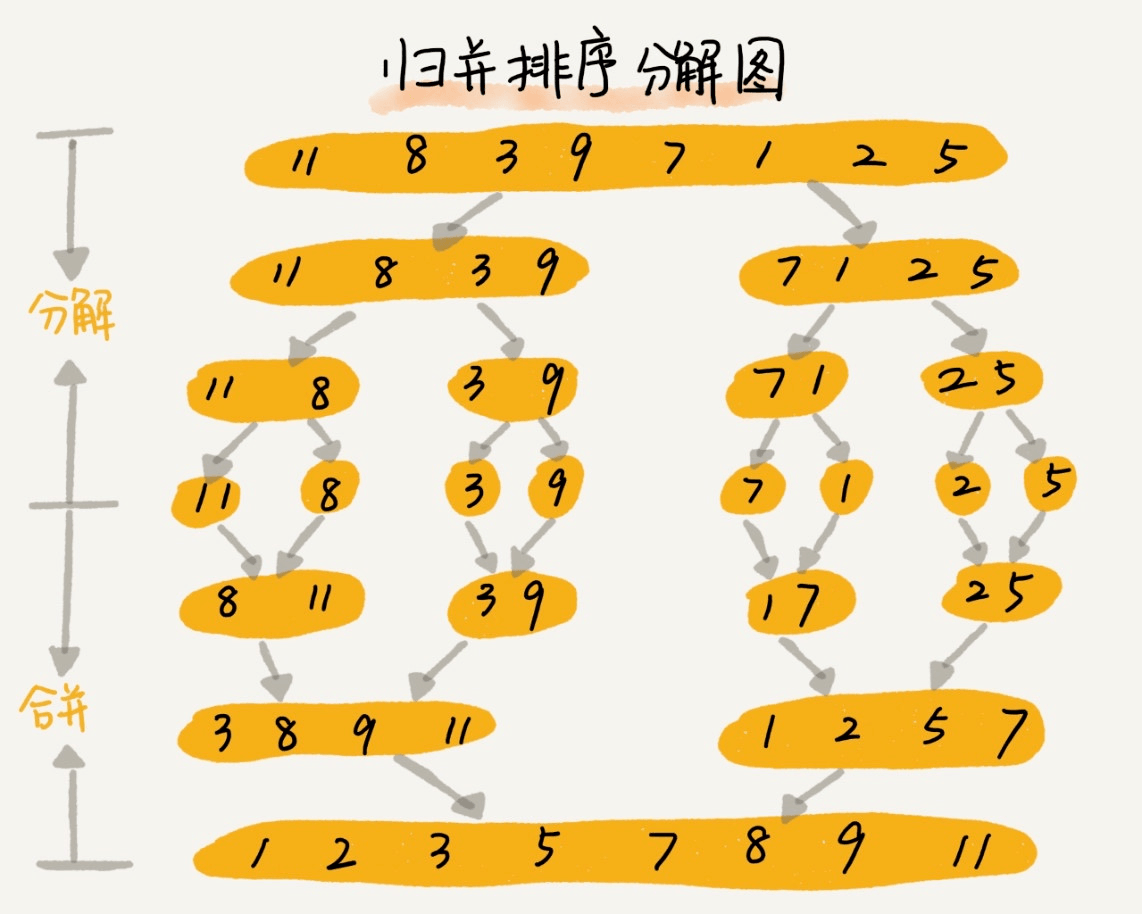
归并排序使用了分治思想

快速排序#

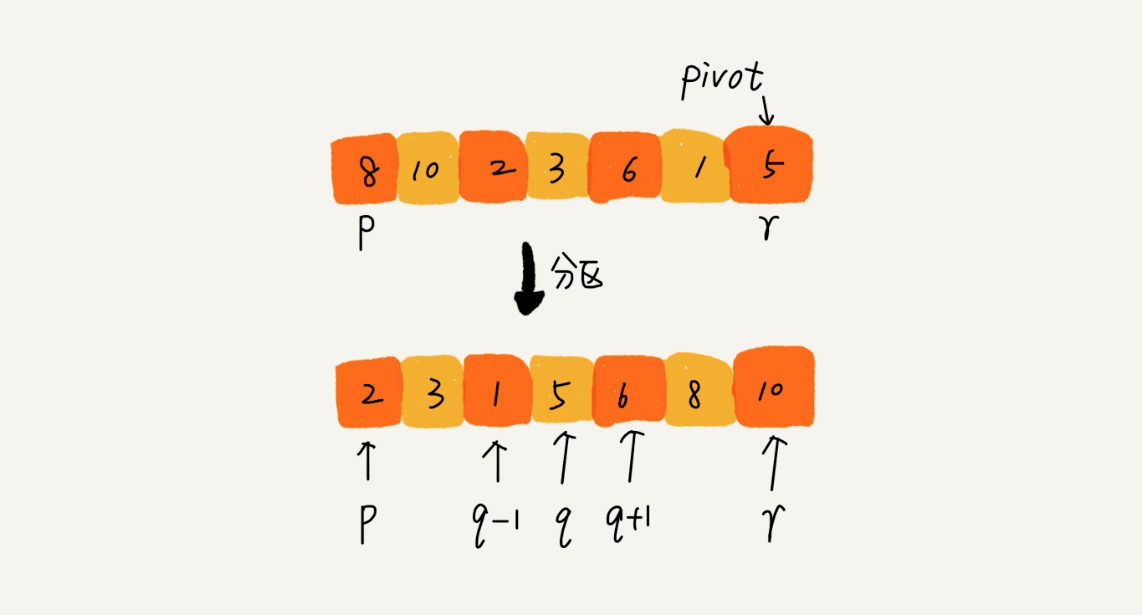
常规排序里综合排名最高的排序算法

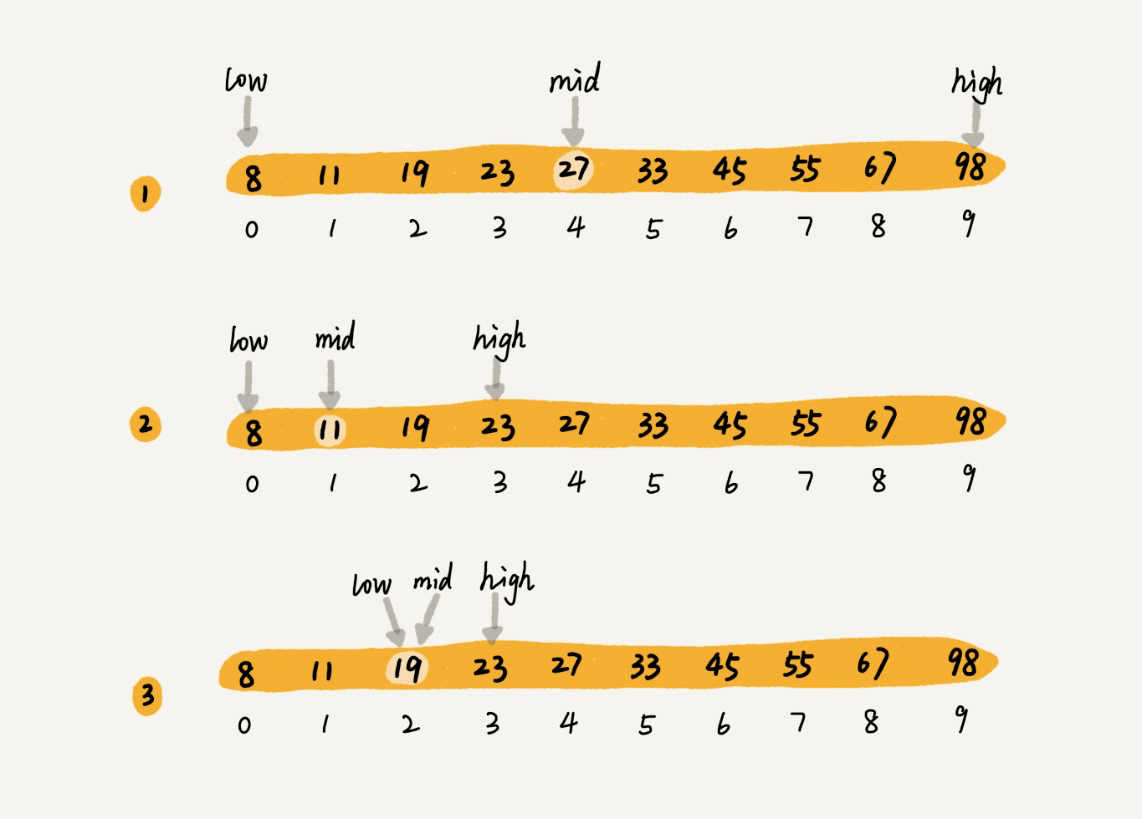
二分查找#

稠密索引（数据库索引技术基础）#

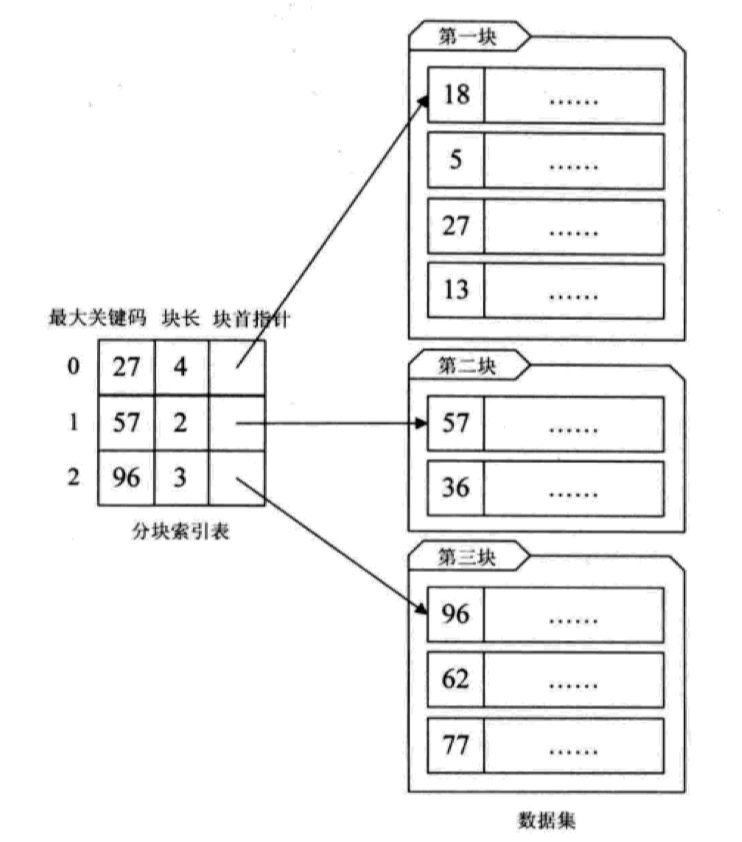
分块索引（数据库索引技术基础）#

倒排索引（搜素引擎技术基础）#

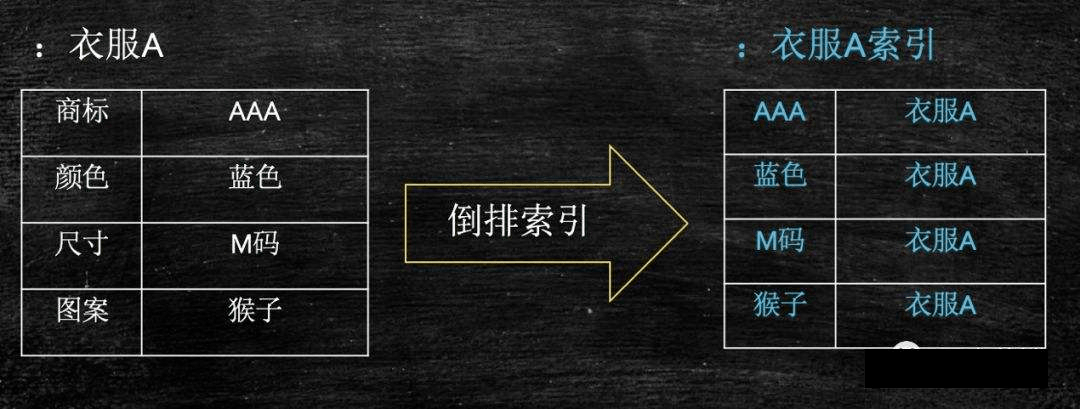
在涉及中文的文章中，还要进行中文分词
应用：比如 Elasticsearch、Lucene

散列表#

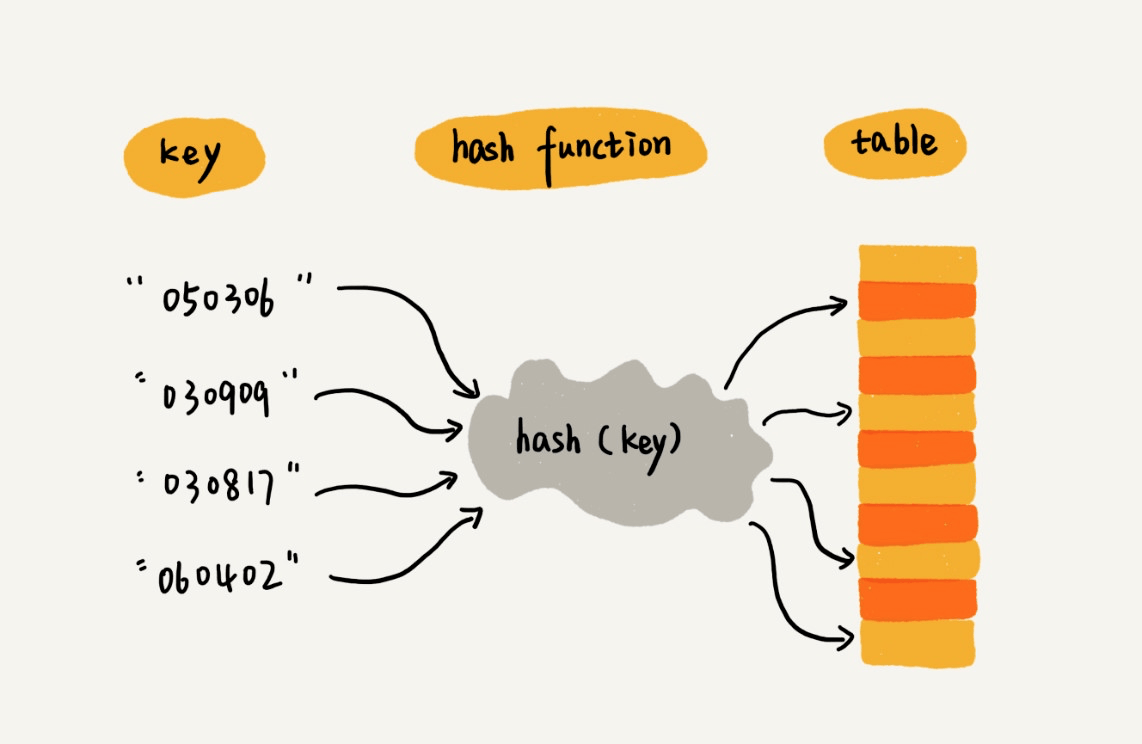
散列冲突解决办法：开放寻址法在数据量较小、装载因子小的时候（小于 1）选用；链表法可以容忍装载因子大于 1，适合存储大对象、大数据量的散列表，且更加灵活，支持更多优化策略。
应用：安全加密、唯一标识、数据校验、散列函数、负载均衡、分布式缓存

字符串匹配算法之 BF 算法#

字符串匹配算法之 KMP 算法#

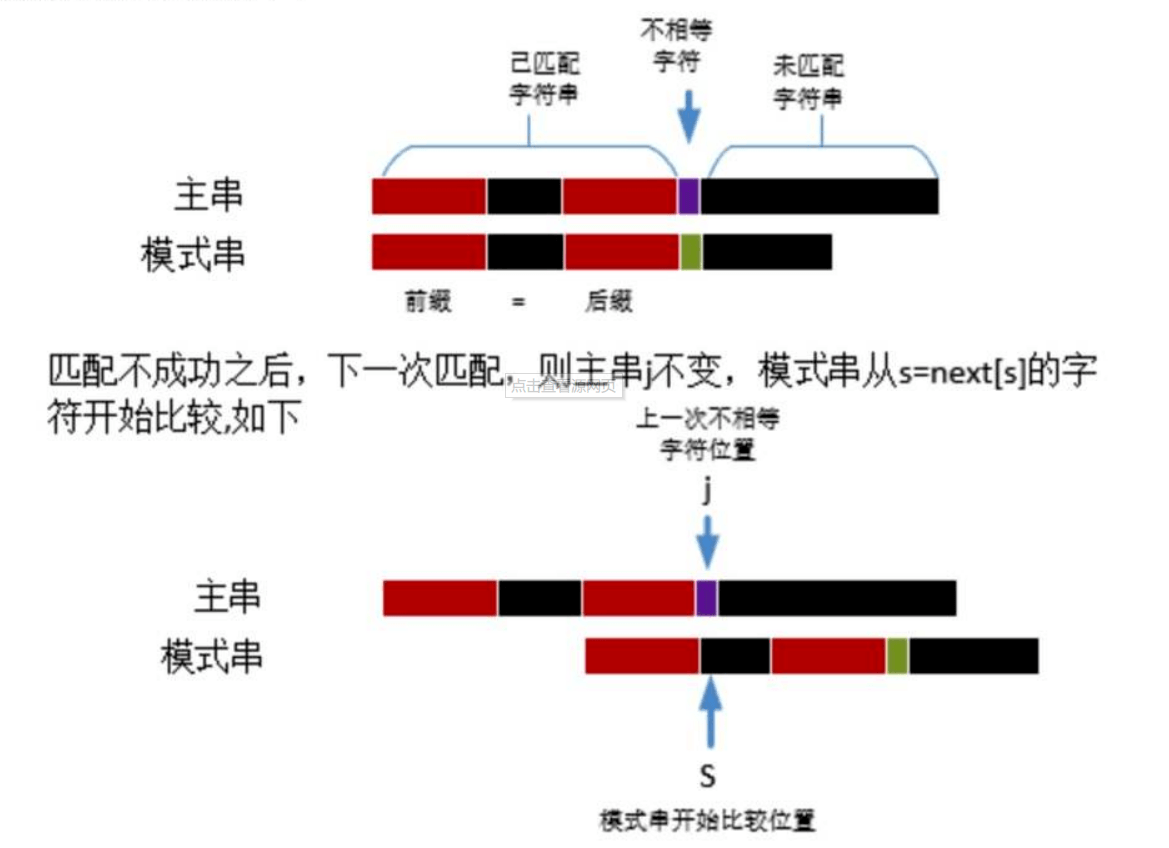
字符串匹配算法之 Trie 树#

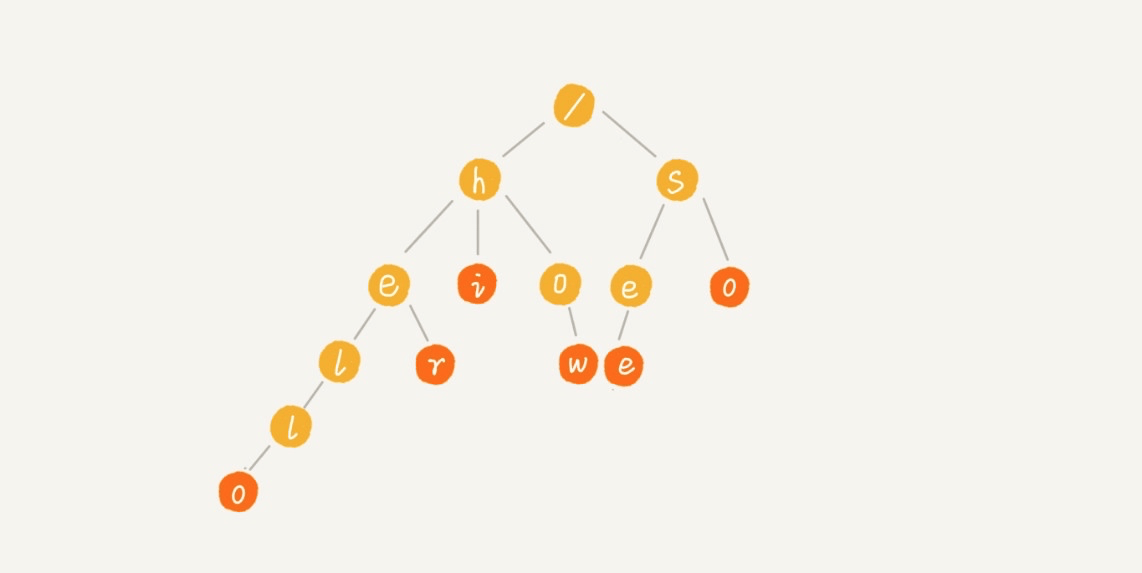
应用：敏感词过滤系统、搜索框联想功能、浏览器网址输入自动补全、IDE 代码编辑器自动补全、输入法自动补全功能

二叉树#

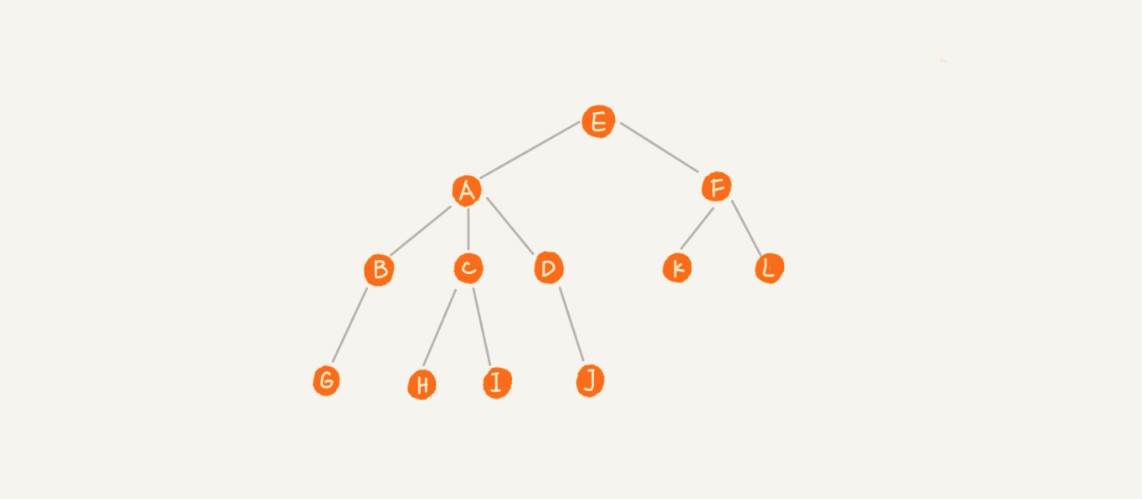
二叉树的存储#

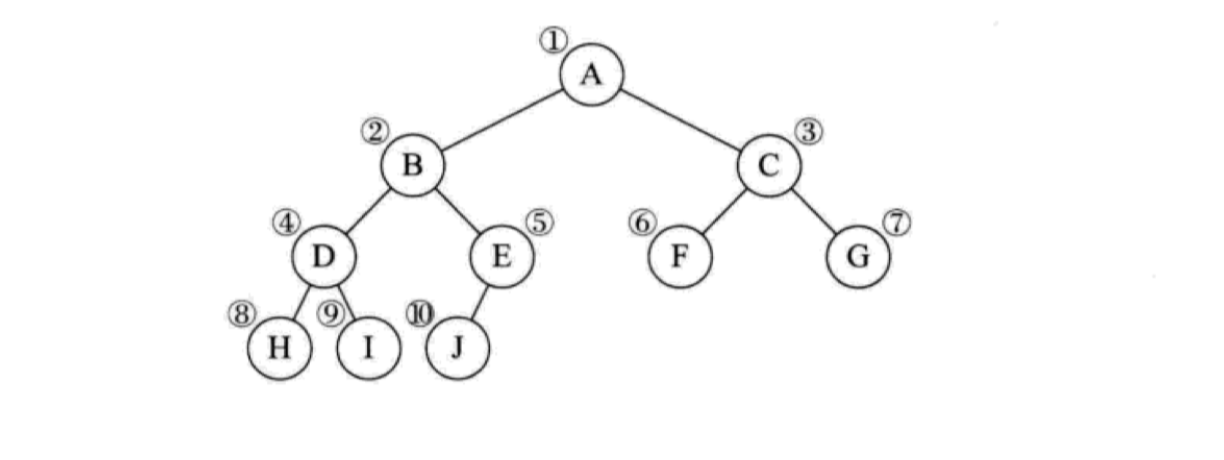
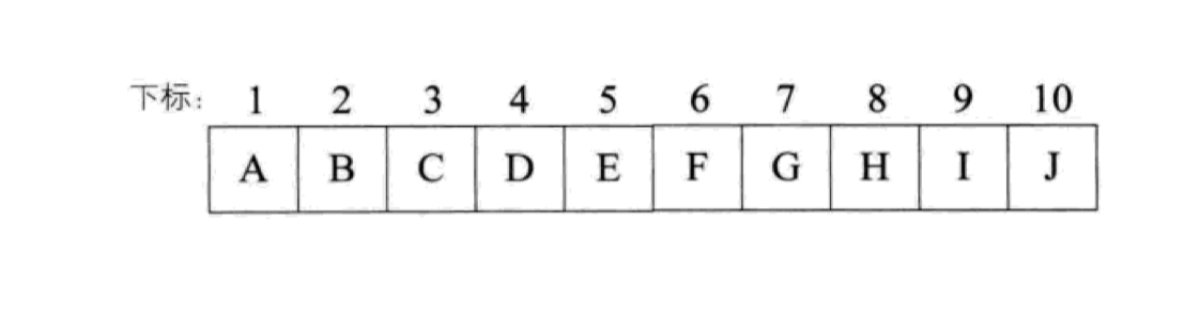
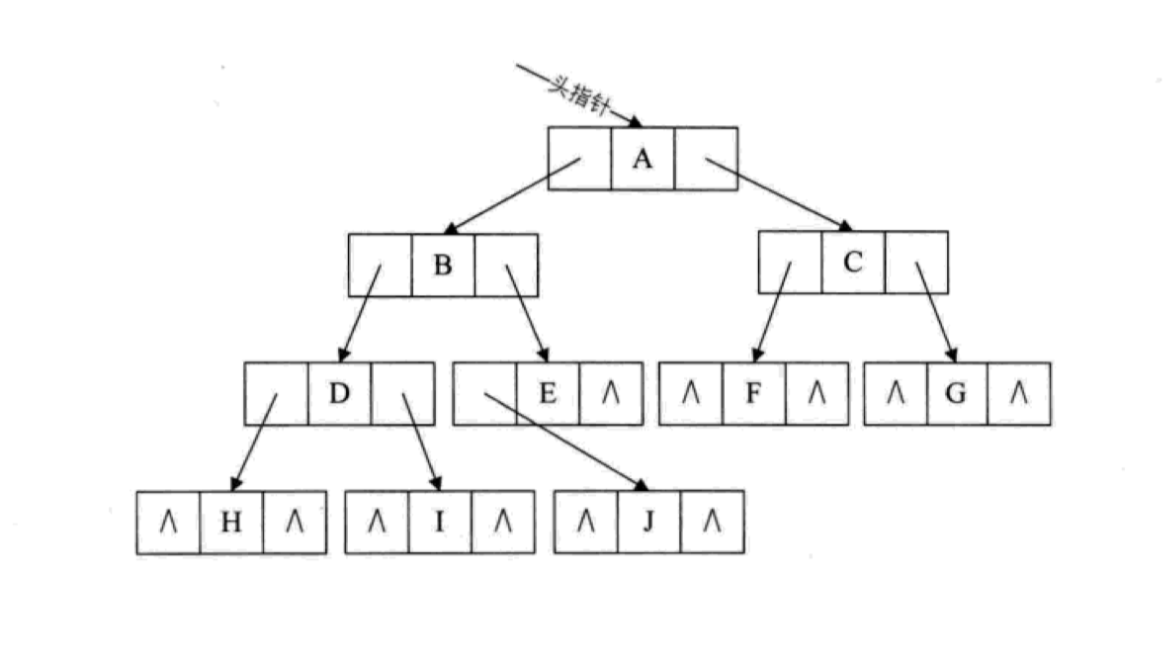
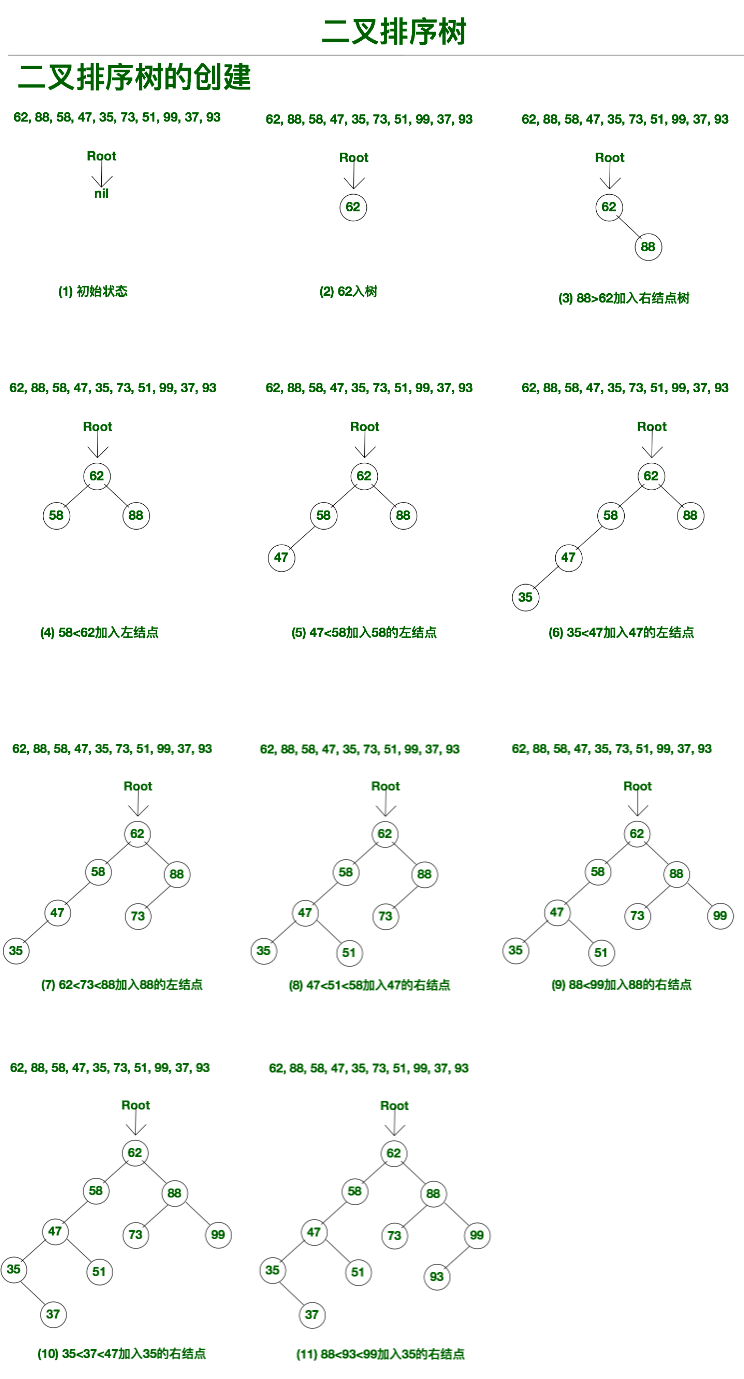
二叉排序（查找）树#

平衡二叉树（AVL）#

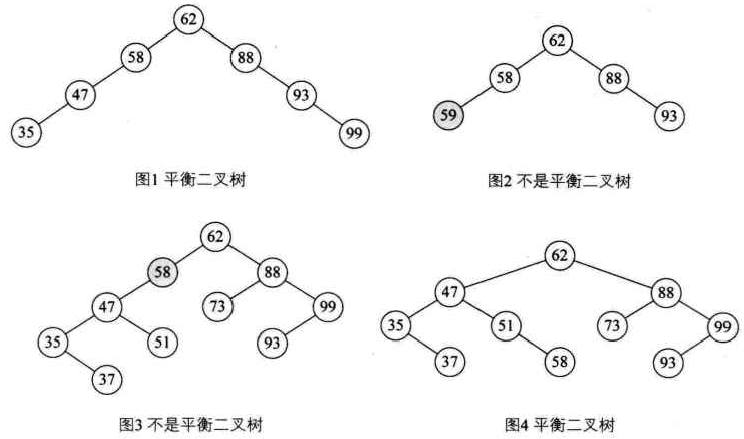
平衡二叉树要求每个节点的左子树和右子树的高度差至多等于 1，这个高度（深度）差的值叫做平衡因子 BF，也就是说 BF 的值不能大于 1，否则就不是平衡二叉树。
如果平衡因子小于 -1，即右子树高度值比较大，则需要左旋：

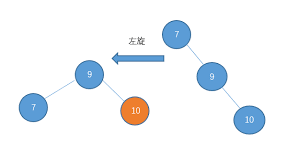
反之，如果平衡因子大于 1，即左子树高度值比较大，则需要右旋：

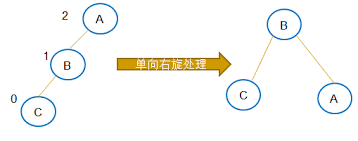
四种调整方式：LL（右旋）、RR（左旋）、LR（先右旋再左旋）、RL（先左旋再右旋）

平衡二叉树性能是最好的，也是最稳定的，但是这套算法实现起来比较复杂，每次插入节点和删除节点都需要判断剩下节点构成的二叉排序树是否满足平衡二叉树的要求，如果不满足需要做相应的左旋右旋处理，维护成本高，因此，在工程实践上，我们更多时候使用的是红黑树这种二叉排序树，它是一种不严格的平衡二叉树，实现起来更加简单，性能也接近严格的平衡二叉树

红黑树#

• 节点是红色或黑色；
• 根节点是黑色的；
• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
• 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

下面是一个典型的红黑树示例：

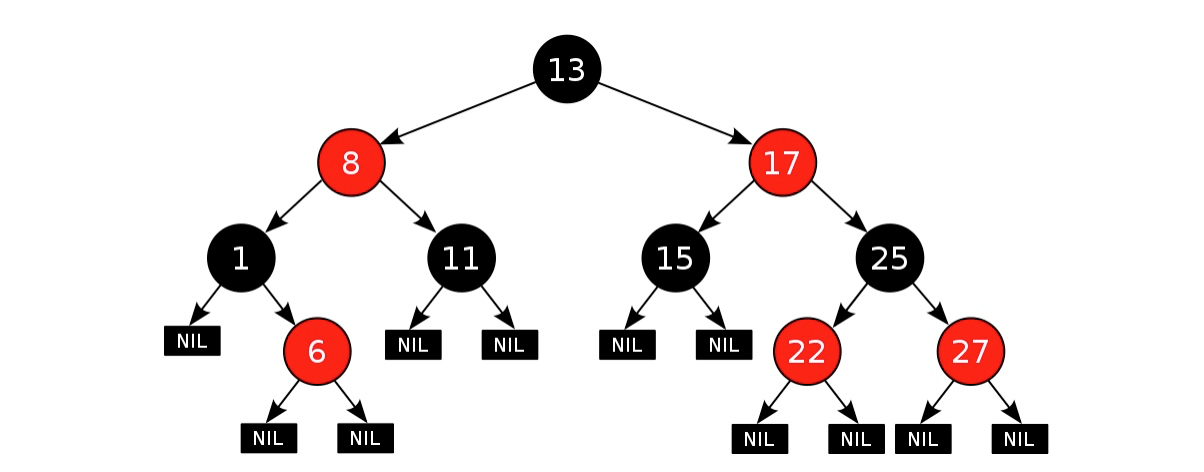
应用：
1. 著名的 linux 进程调度，用红黑树管理进程控制块
2.epoll 在内核中的实现，用红黑树管理事件块
3.nginx 中，用红黑树管理 timer 等
4.Java 的 TreeMap 实现
5. 广泛用在 C++ 的 STL 中。map 和 set 都是用红黑树实现的。

压缩算法的基础：赫夫曼树#

哈夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树。

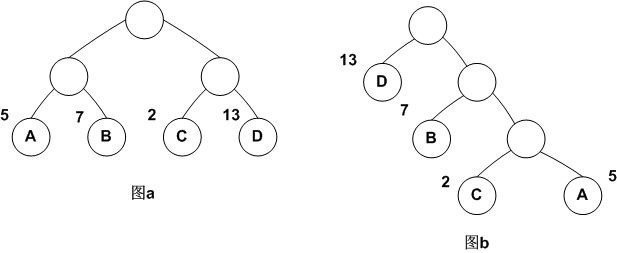
它们的带权路径长度分别为：

图 a： WPL=5 * 2 + 7 * 2 + 2 * 2 + 13 * 2=54

图 b： WPL=5 * 3 + 2 * 3 + 7 * 2 + 13 * 1=48

可见，图 b 的带权路径长度较小，我们可以证明图 b 就是哈夫曼树 (也称为最优二叉树)。

图#

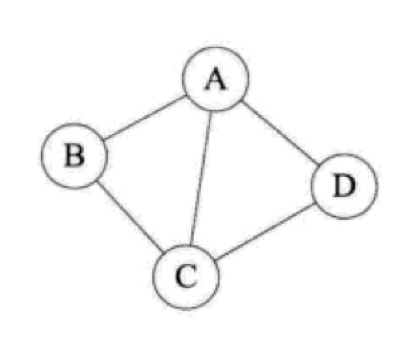
应用场景：比如社交网络中用户之间的关系，网络设备之间的拓扑结构，以及显示生活中形形色色的网：公路网、铁路网、地铁网等等，都可以通过图来表示。

图的存储#

邻接矩阵#

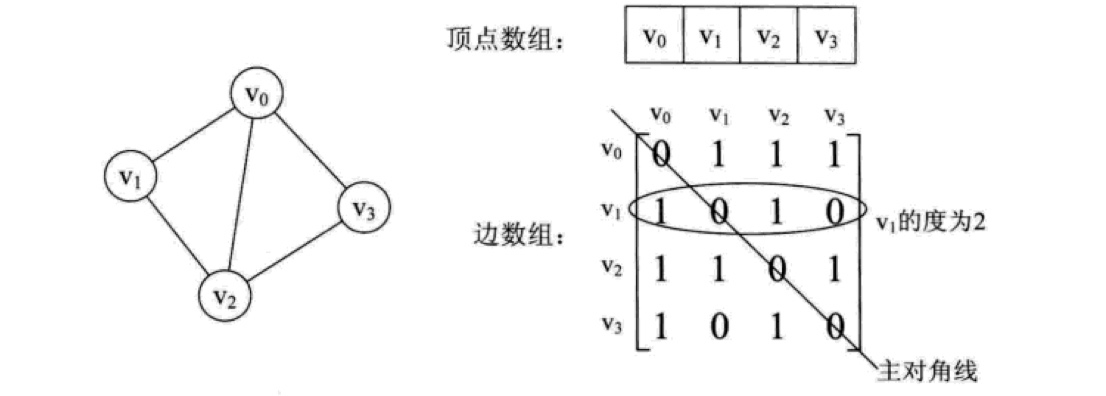
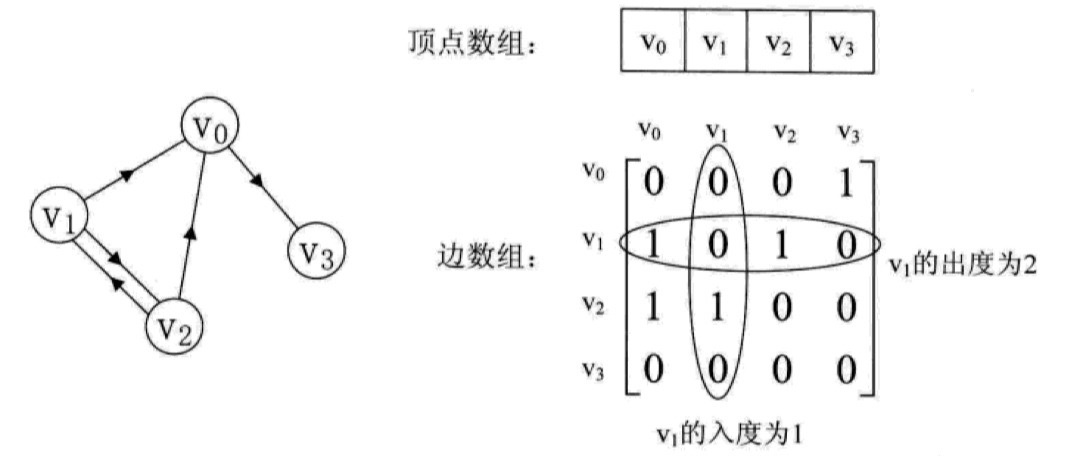
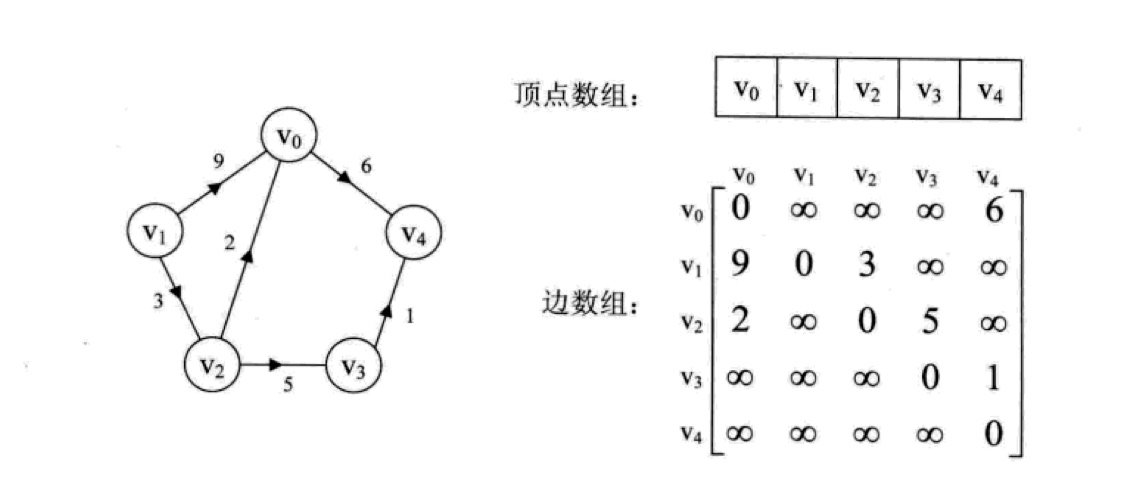
对于有 n 个顶点的图而言，时间复杂度是 O(n^2)，空间复杂度也是如此，而且如果图比较稀疏的话（稀疏图），边数组会存在巨大的空间浪费。但是优点是实现起来非常简单，对于稠密图或者非常简单的图来说，用邻接矩阵是比较方便的。

邻接表#

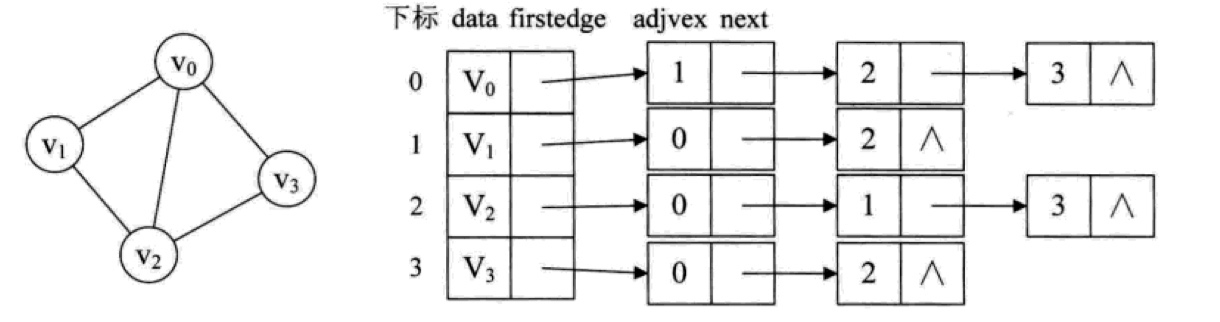
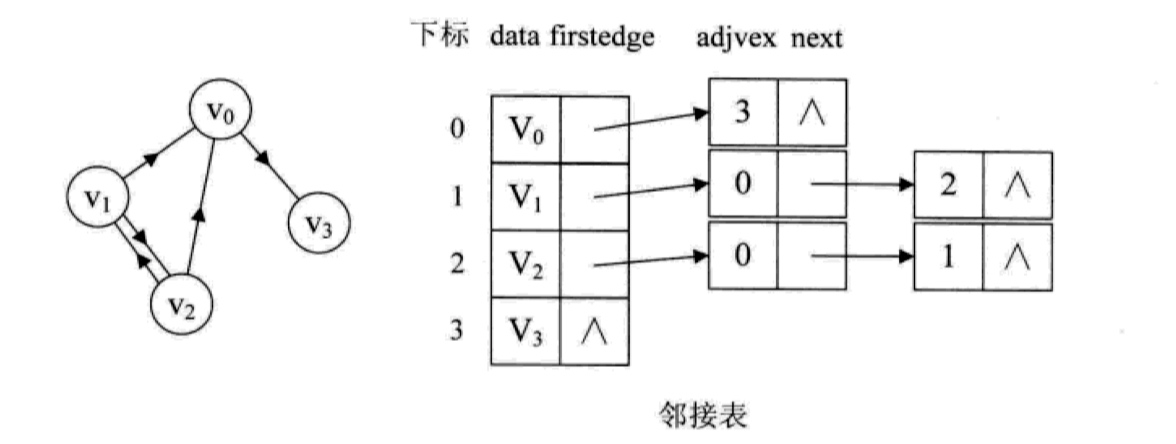
邻接表的构建时间复杂度要比邻接矩阵好，对于一个有 n 个顶点和 e 条边的图而言，时间复杂度是 O(n+e)，而且不存在任何空间的浪费，比较高效，可用于存储任何图。

图的遍历 —— 深度优先搜索#

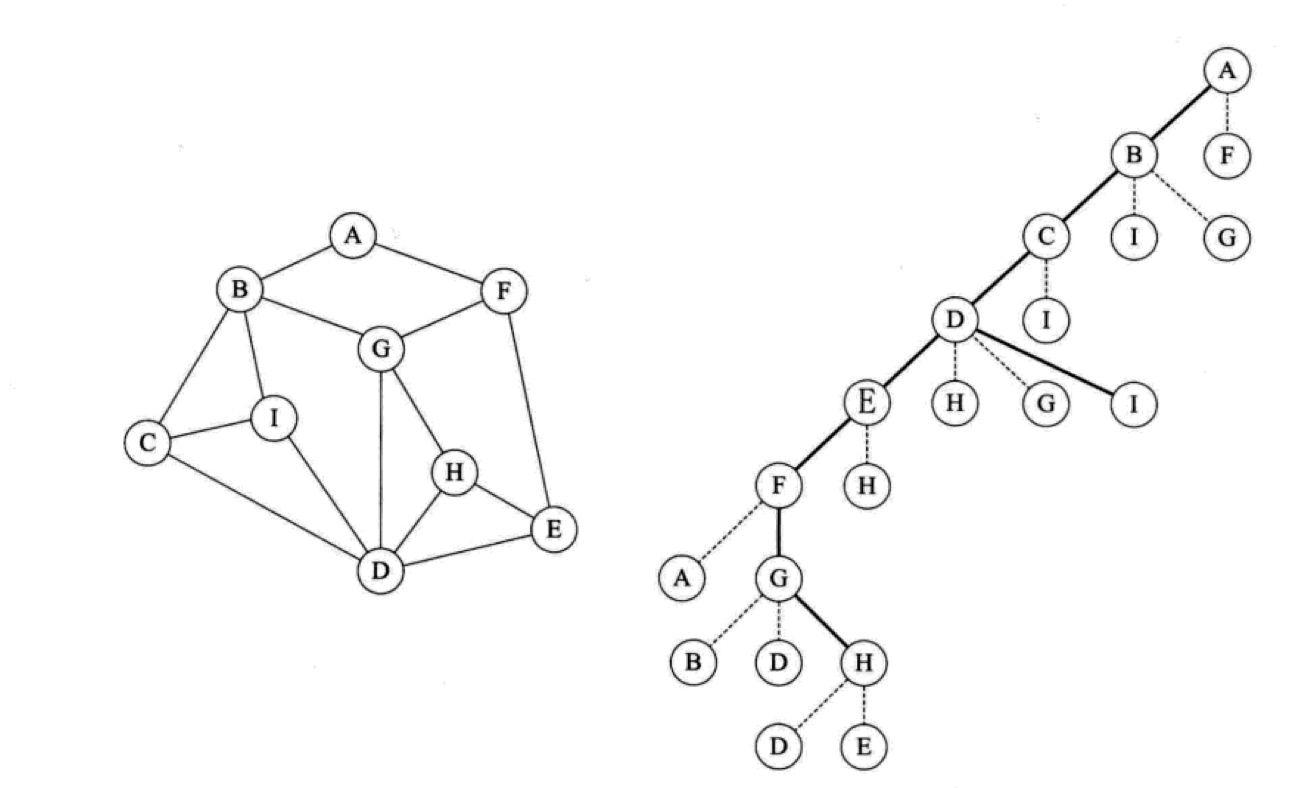
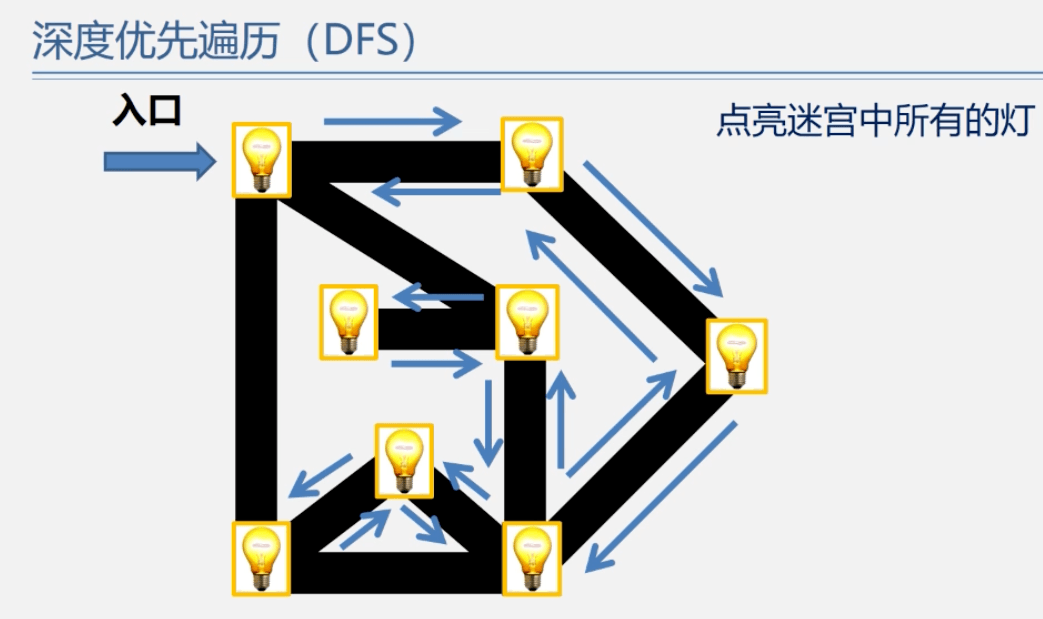
图的遍历 —— 广度优先搜索#

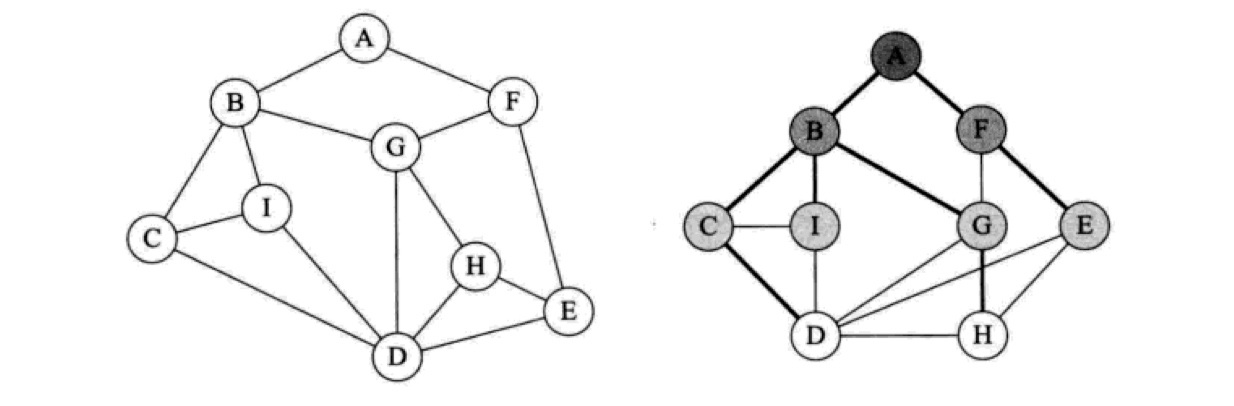
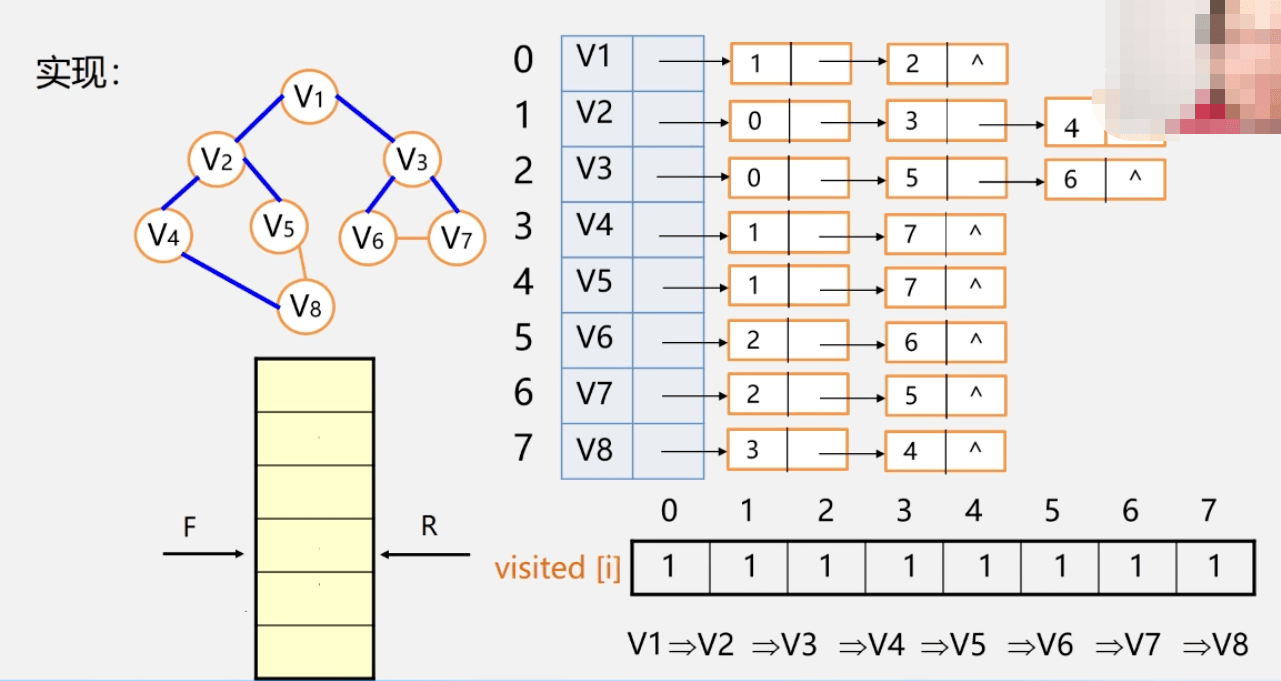
广度优先搜索的时间复杂度和深度优先搜索一样，也是 O(v+e)，其中 v 表示顶点数，e 表示边数，需要额外的数组存储已访问顶点和前驱顶点，对应的空间复杂度是 O(v)。
广度优先搜索和深度优先搜索的复杂度完全一样，没有优劣之分，具体使用哪种搜索方式，以实际情况为准。

最小生成树#

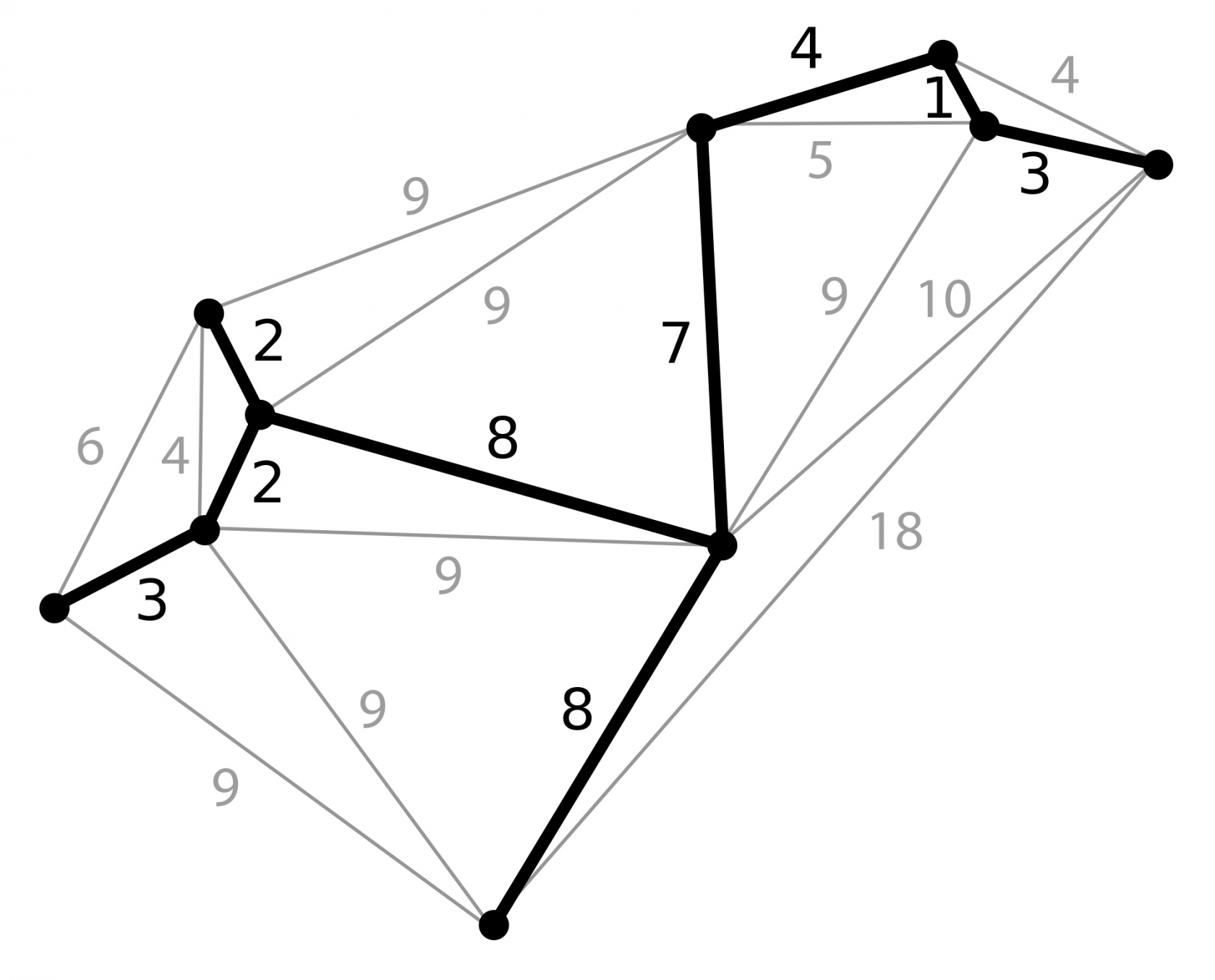
应用场景：规划路径让交通费用最低，国家的电力网、公路网、通信网，规划路径让建设成本最低，计算出最佳路径，连接网络中所有节点的最优路径问题，都可以通过最小生成树来处理。

最小生成树的实现算法之普里姆算法（Prim）#

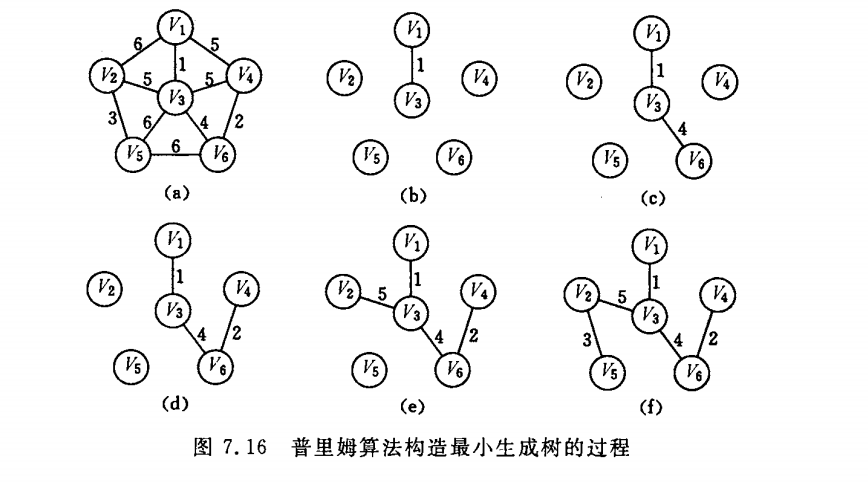
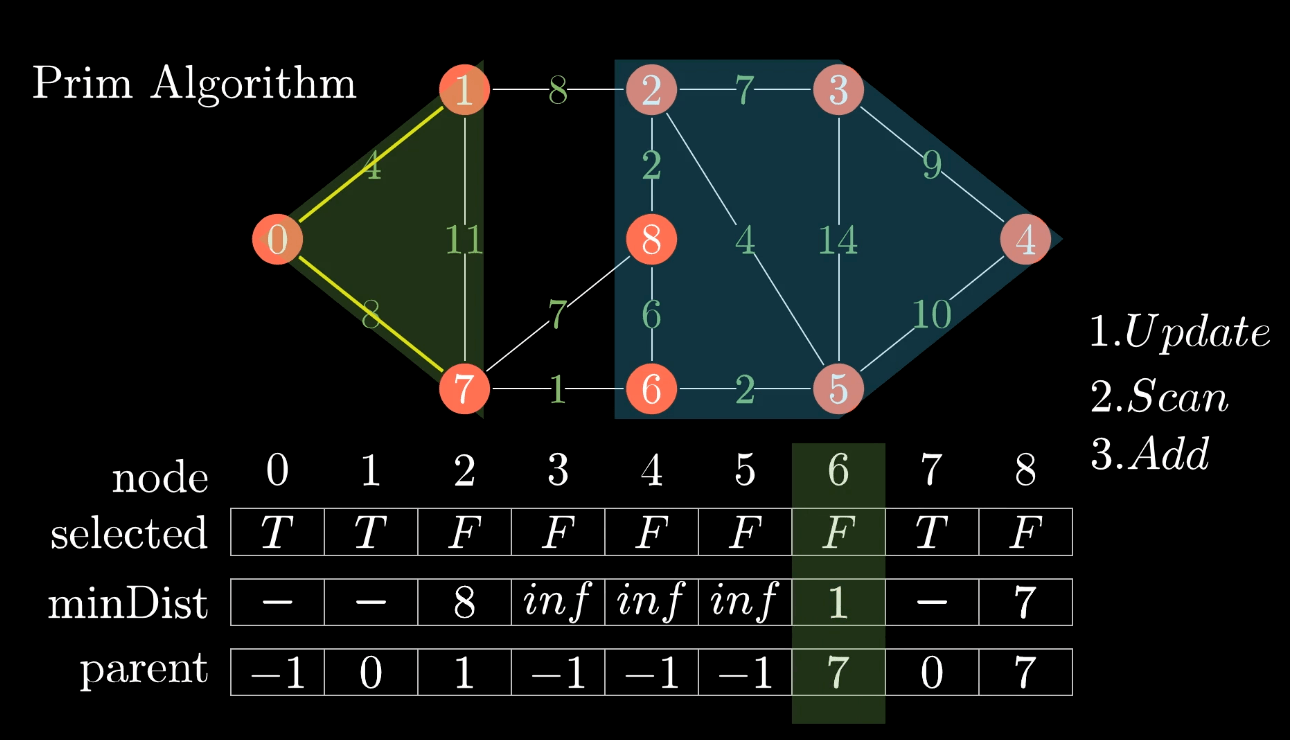
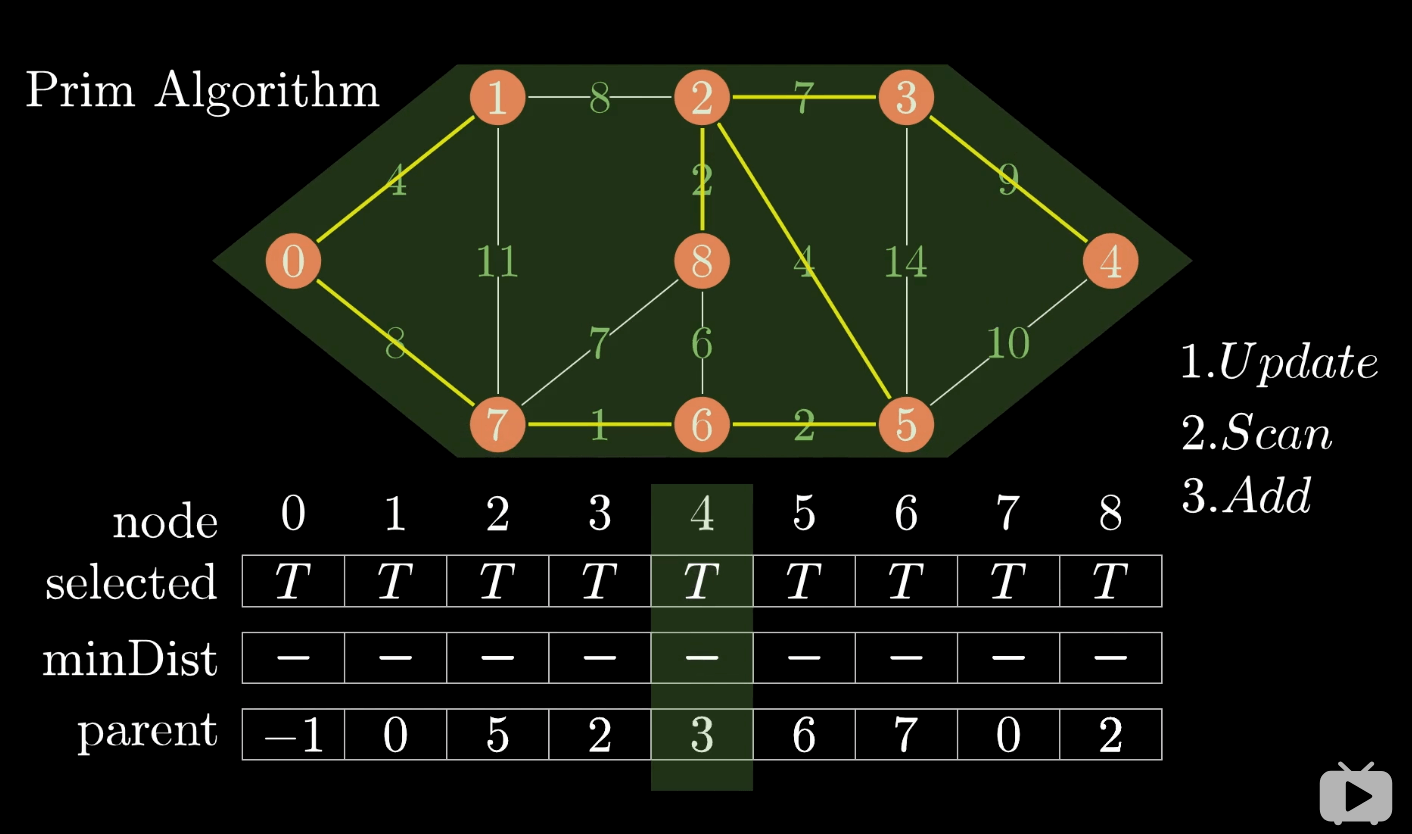
最小生成树 prim 算法采用了贪心策略

最小生成树的实现算法之克鲁斯卡尔算法（Kruskal）#

---

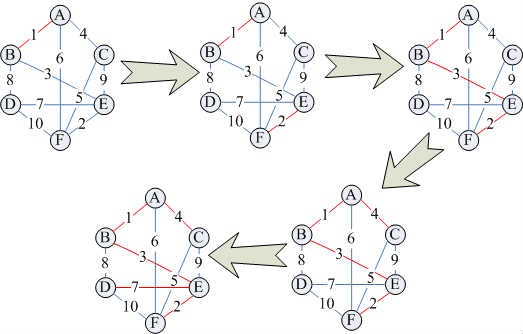
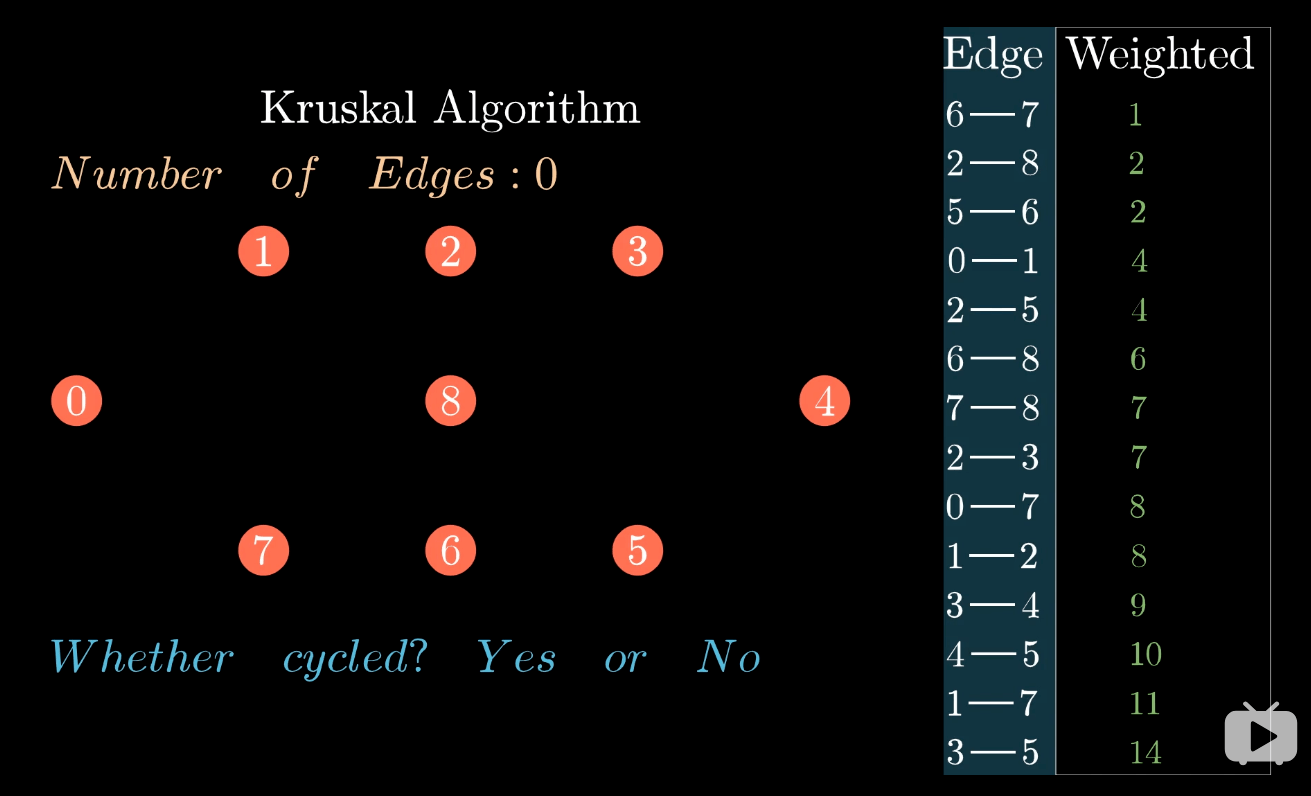
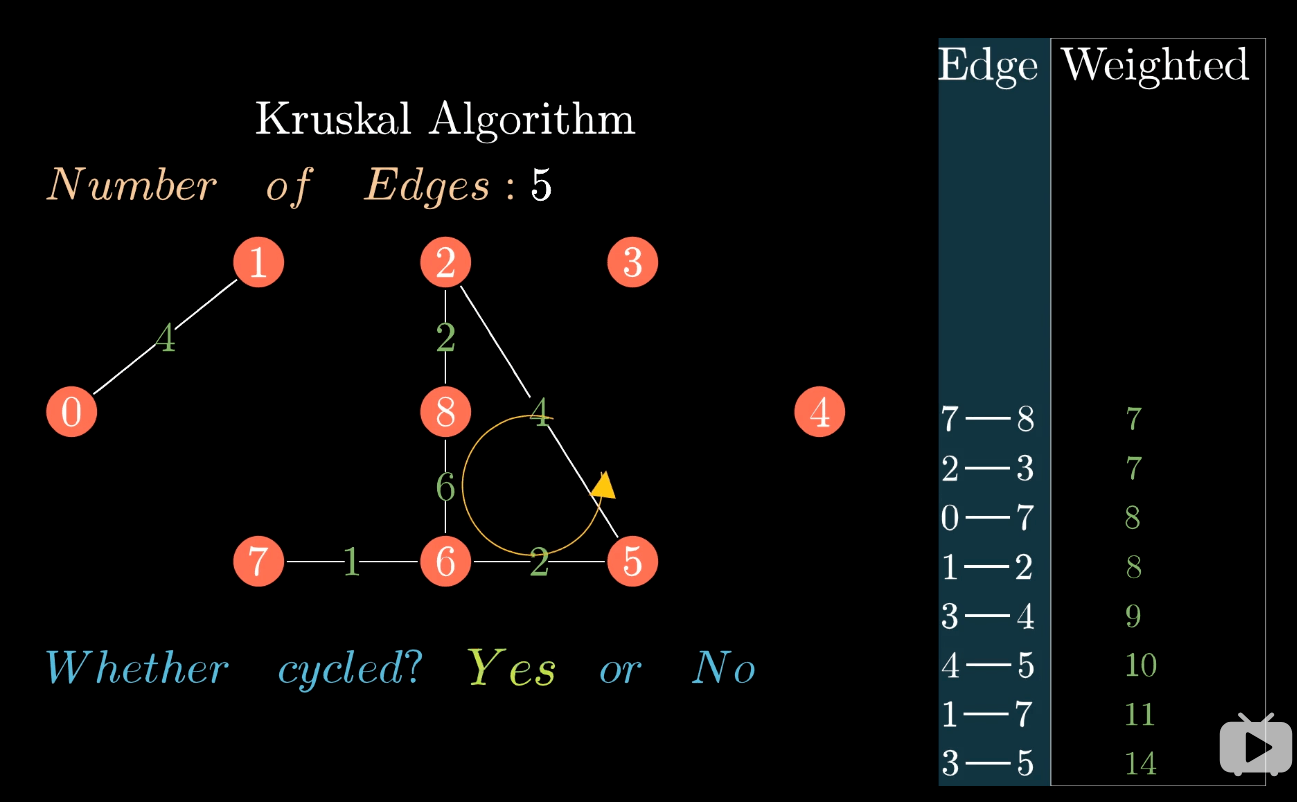
组成环则丢弃

直到选择了 N-1 条边即完成

最短路径及实现算法（一）：迪杰斯特拉算法（Dijkstra）#

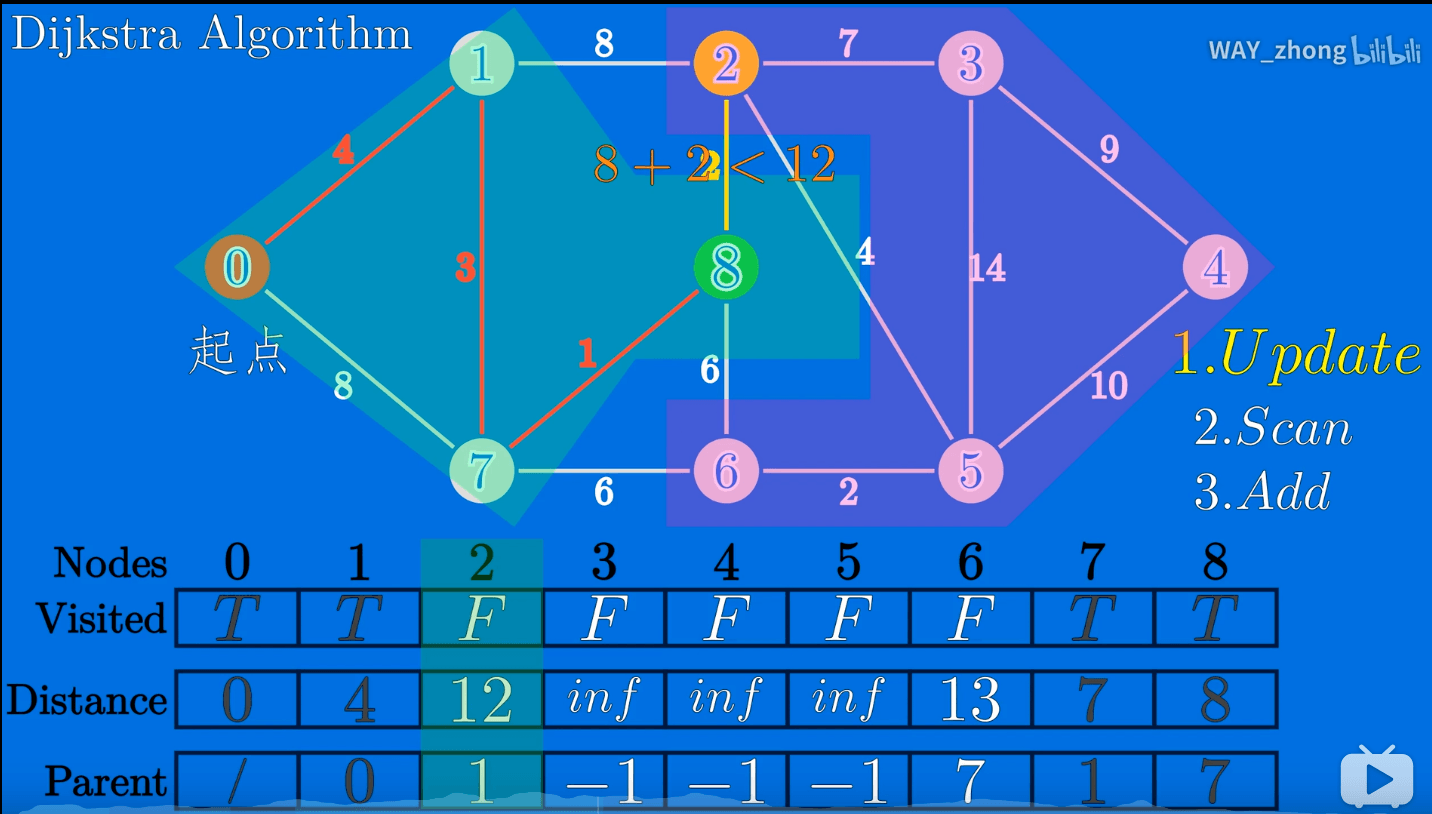
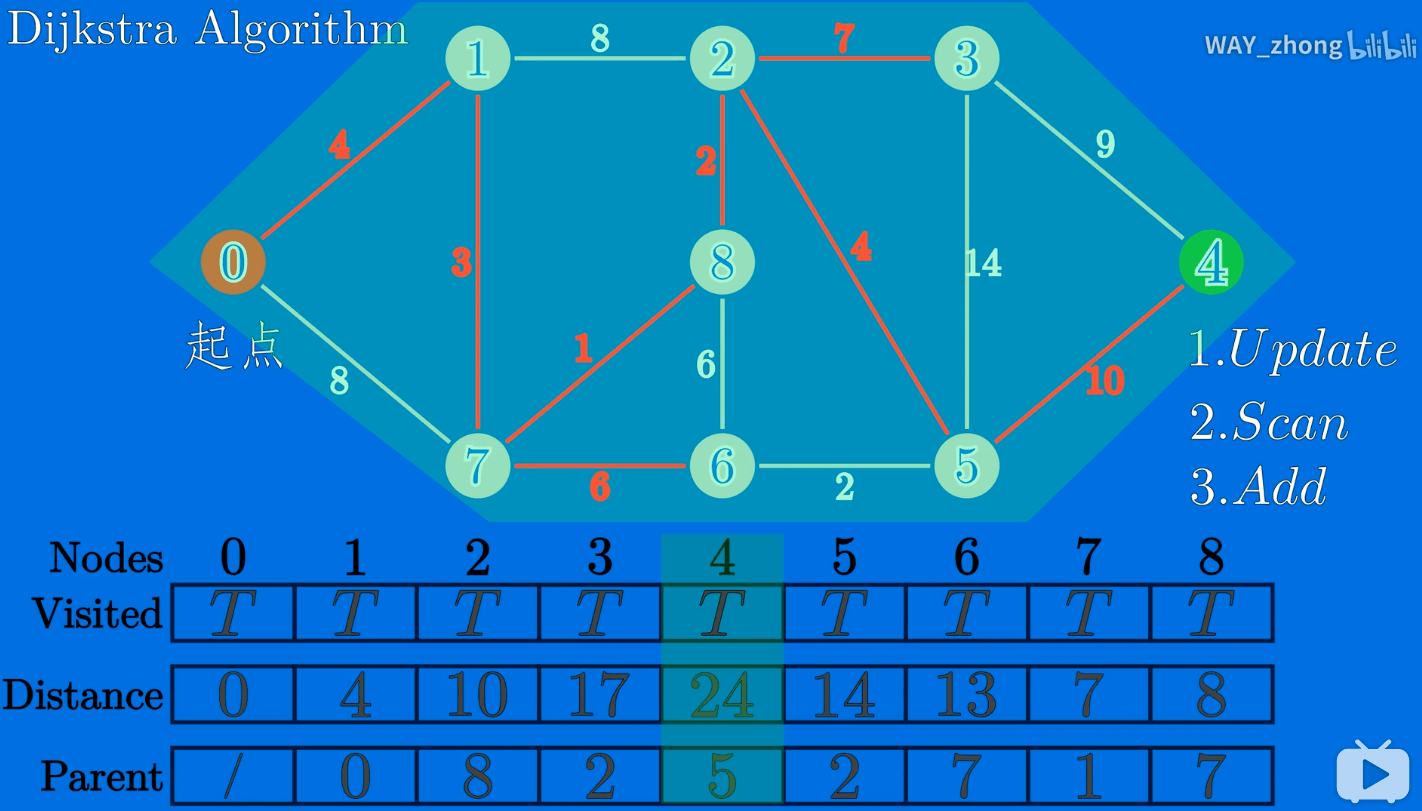
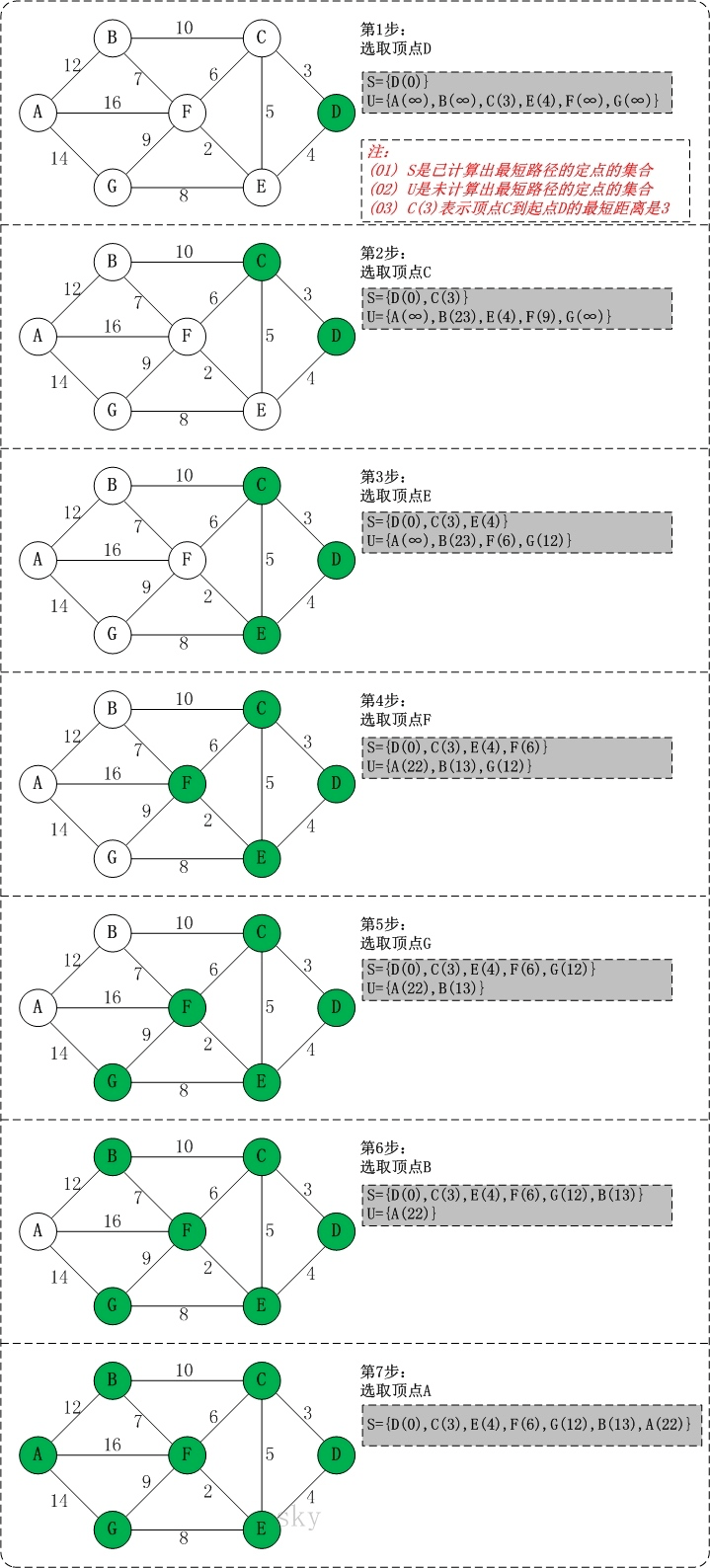
贪心策略
和 prim 算法很类似，Dijkstra 计算距离是累加

最短路径的实现算法（二）：弗洛伊德算法（Floyd）#

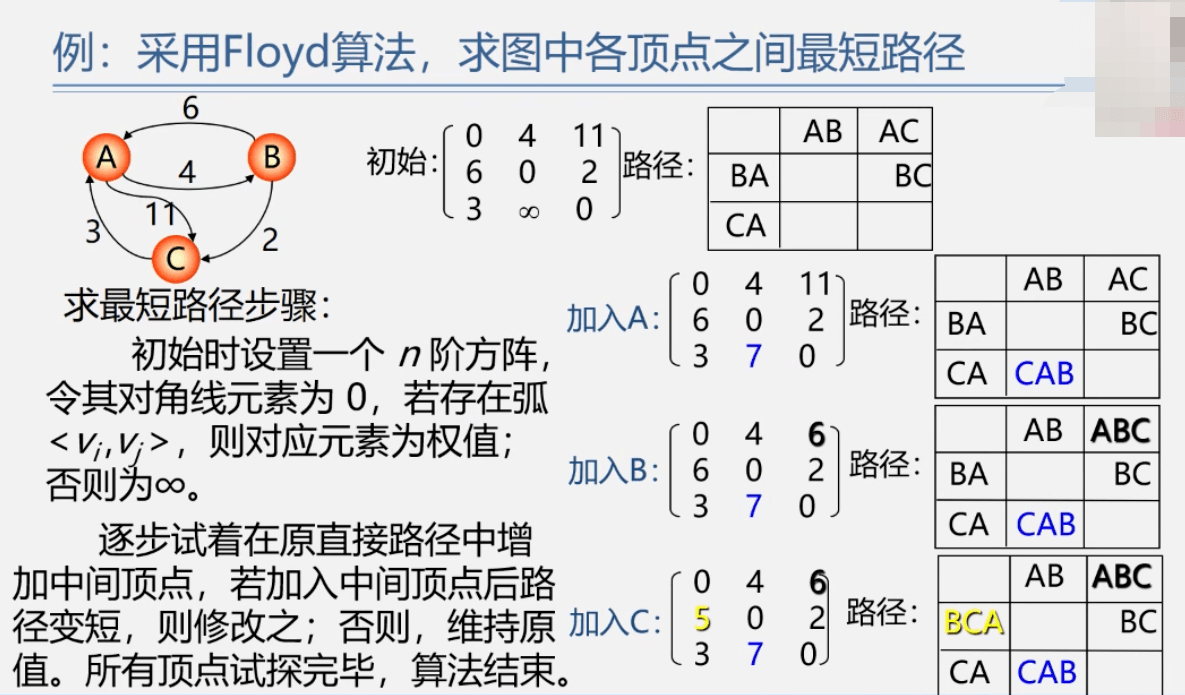
动态规化思想

prim，kruskal 和 dijkstra 算法有贪心策略

1. prim：每次执行都选择轻边
2. kruskal：每次执行都选择权值最小的边，同时合并两个不相交的子集
3. dijkstra：每次执行都选择路径最短 d (s,t)，并将顶点 t 加入到集合 S 中，同时对边进行松弛

拓扑排序（AOV 网）#

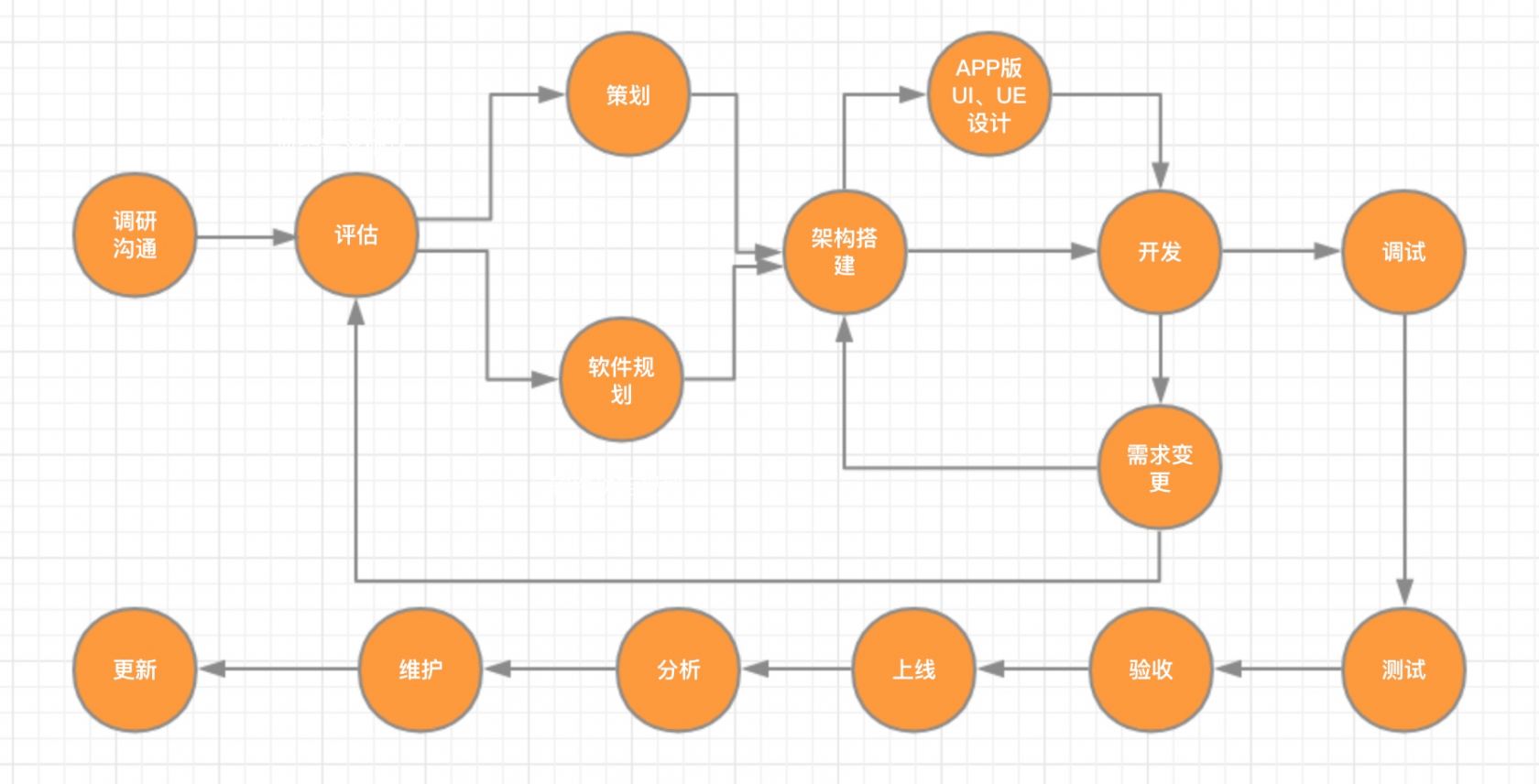
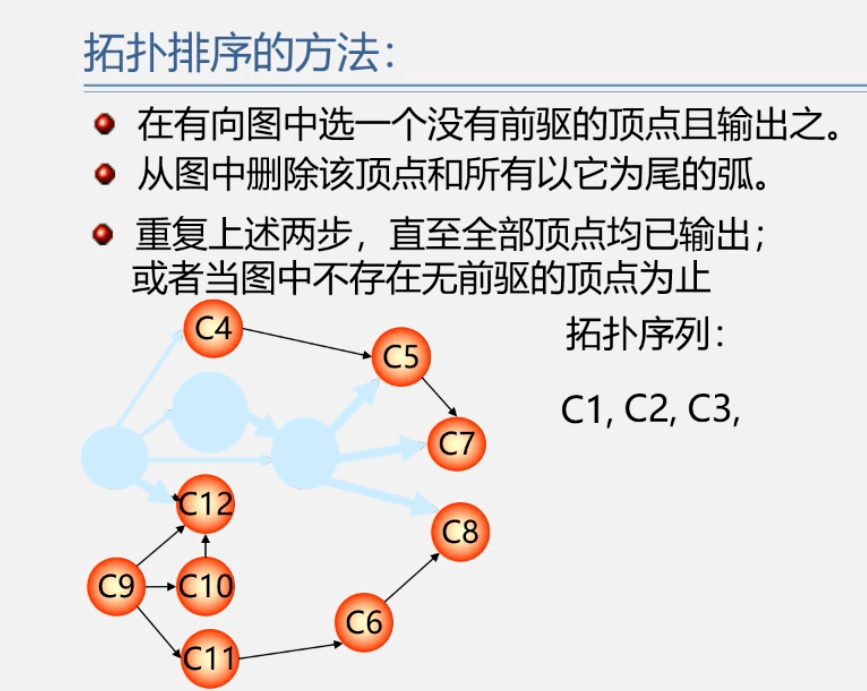
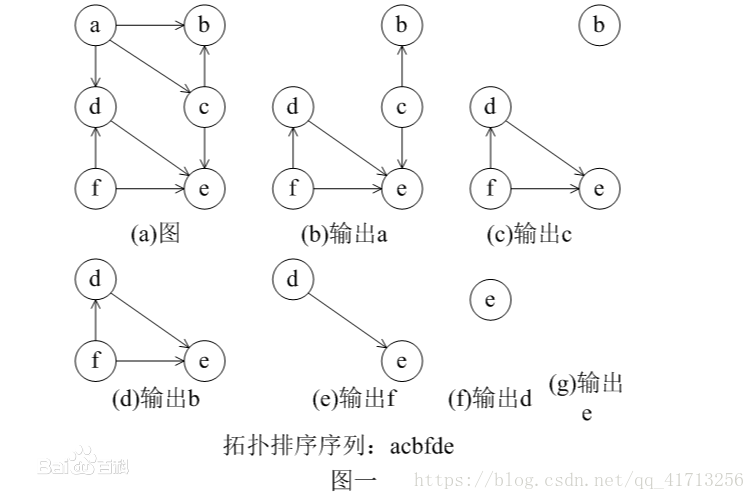
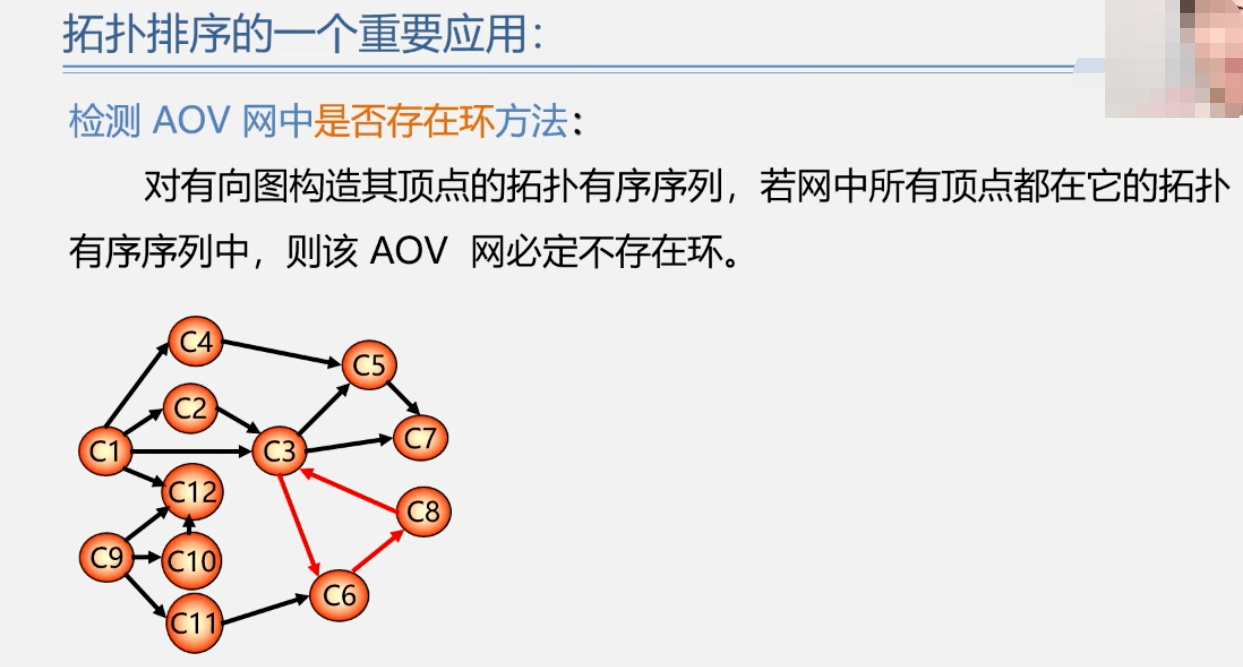
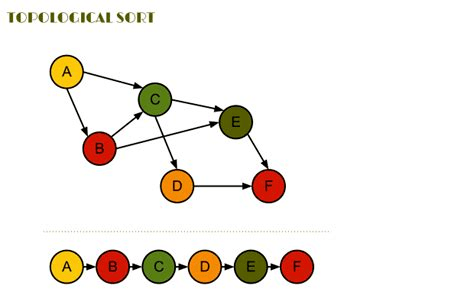
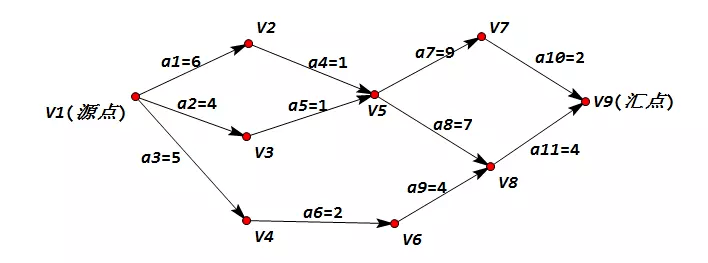
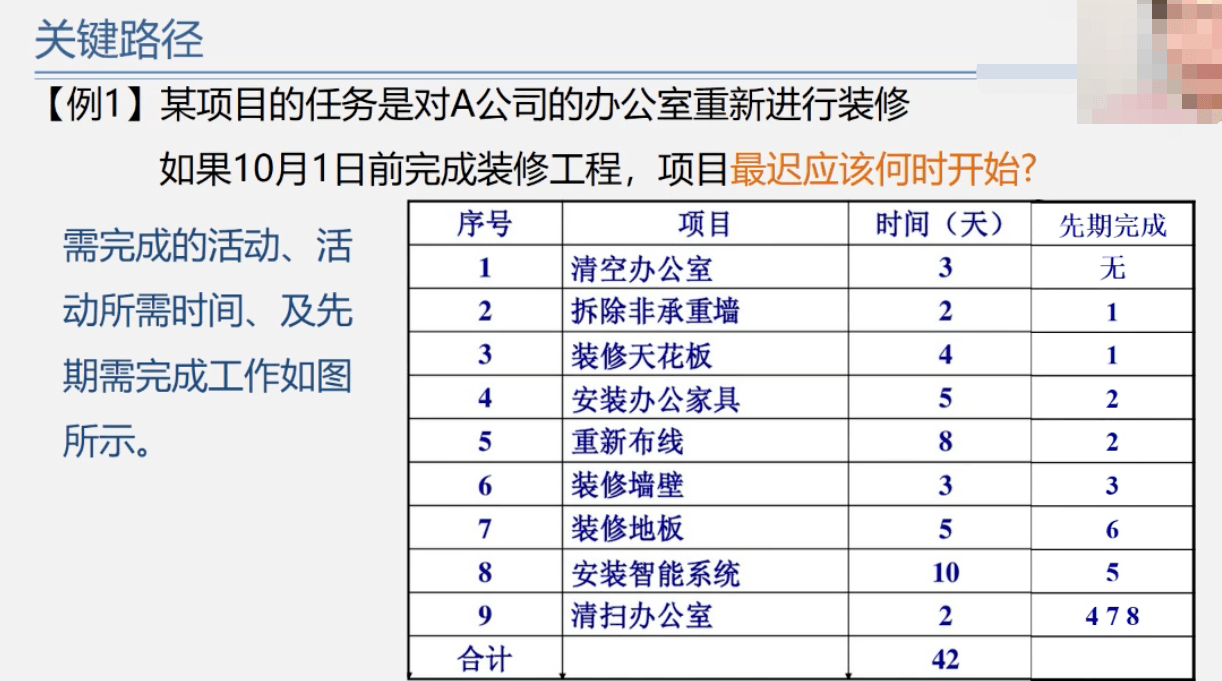
关键路径#

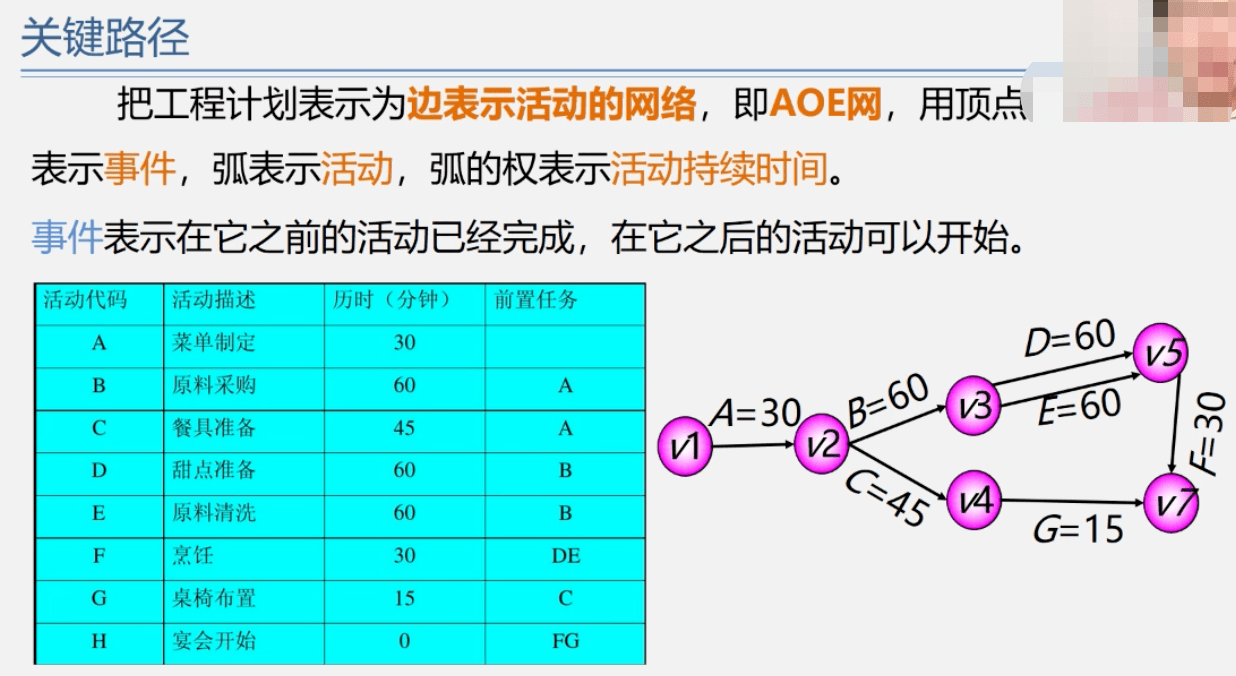
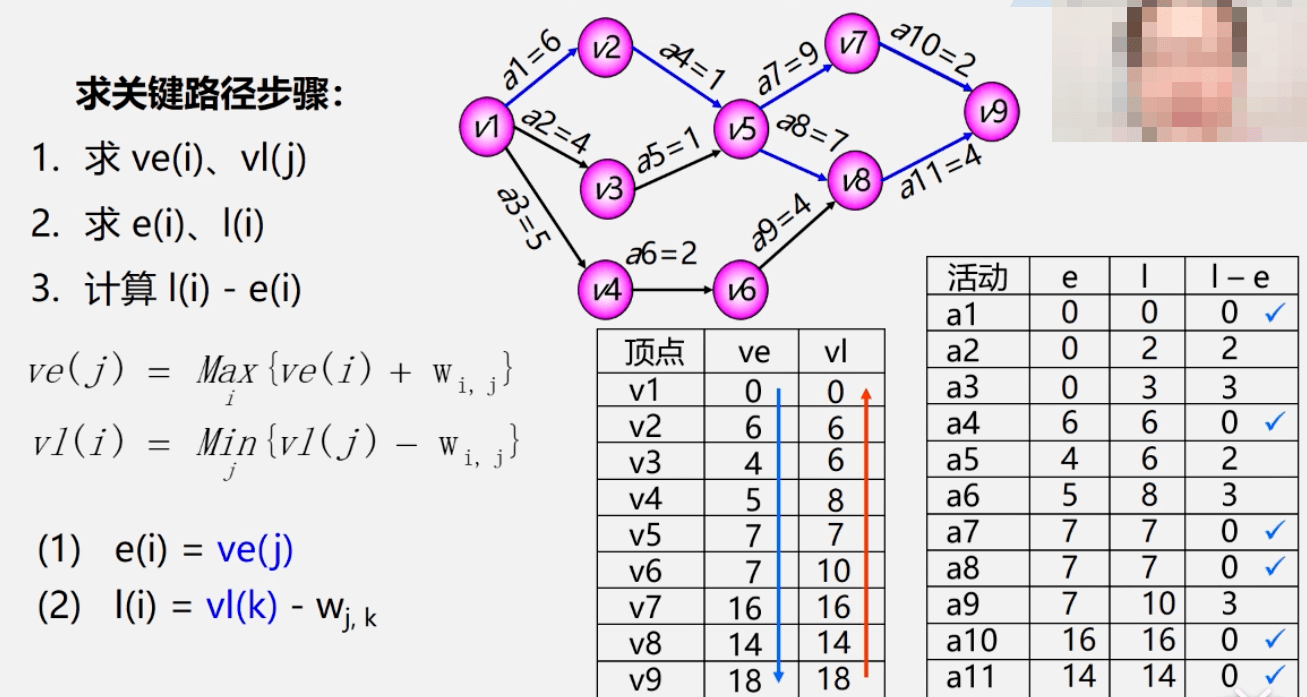
以上内容大部分来自于《学院君 - 数据结构与算法》

本作品采用《CC 协议》，转载必须注明作者和本文链接