数据结构与算法整理总结---散列表

散列表⽤的是数组⽀持按照下标随机访问数据的特性，所以散列表其实就是数组的⼀种扩展，由数组演化⽽来。可以说，如果没有数组，就没有散列表。

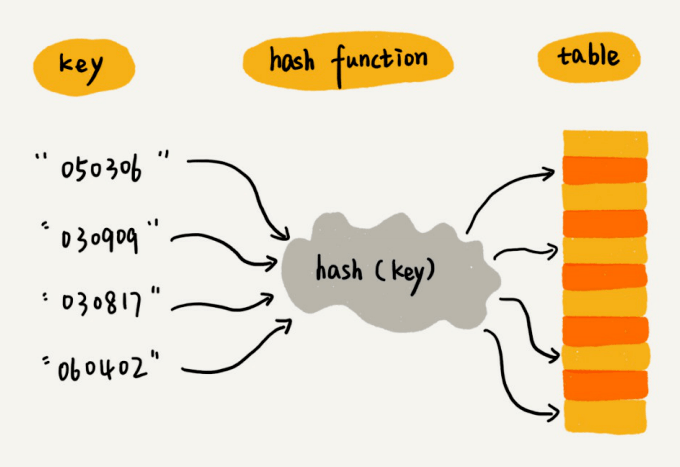
散列表⽤的就是数组⽀持按照下标随机访问的时候，时间复杂度是O(1)的特性。我们通过散列函数把元素的键值映射为下标，然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时，我们⽤同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取数据。

散列函数在散列表中起着⾮常关键的作⽤。

散列函数，顾名思义，它是⼀个函数。我们可以把它定义成hash(key)，其中key表示元素的键值，hash(key)的值表示经过散列函数计算得到的散列值。

三点散列函数设计的基本要求：

1. 散列函数计算得到的散列值是⼀个⾮负整数；

2. 如果key1 = key2，那hash(key1) == hash(key2)；

3. 如果key1 ≠ key2，那hash(key1) ≠ hash(key2)。

其中，第⼀点理解起来应该没有任何问题。因为数组下标是从0开始的，所以散列函数⽣成的散列值也要是⾮负整数。第⼆点也很好理解。相同的key，经过散列函数得到的散列值也应该是相同的。

第三点理解起来可能会有问题。这个要求看起来合情合理，但是在真实的情况下，要想找到⼀个不同的key对应的散列值都不⼀样的散列函数，⼏乎是不可能的。即便像业界著名的MD5、SHA、CRC等哈希算法，也⽆法完全避免这种散列冲突。⽽且，因为数组的存储空间有限，也会加⼤散列冲突的概率。

散列冲突

再好的散列函数也⽆法避免散列冲突。那究竟该如何解决散列冲突问题呢？我们常⽤的散列冲突解决⽅法有两类，开放寻址法（open addressing）和链表法（chaining）。

开放寻址法

开放寻址法的核⼼思想是，如果出现了散列冲突，我们就重新探测⼀个空闲位置，将其插⼊。那如何重新探测新的位置呢？我先讲⼀个⽐较简单的探测⽅法，线性探测（Linear Probing）。

当我们往散列表中插⼊数据时，如果某个数据经过散列函数散列之后，存储位置已经被占⽤了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为⽌。

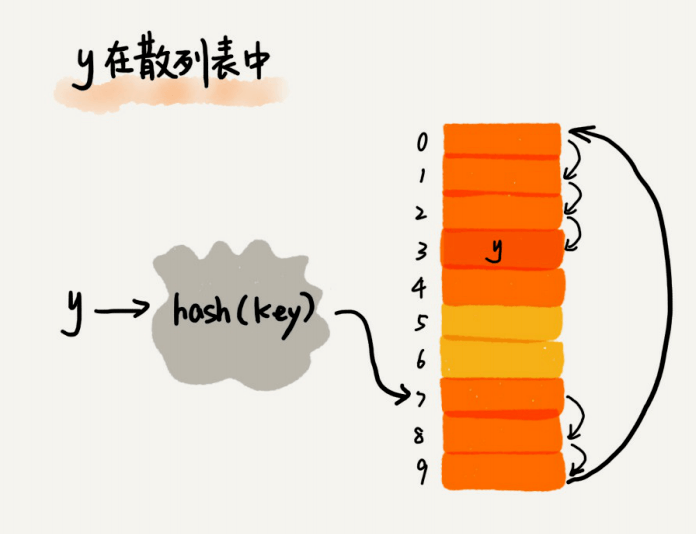
从图中可以看出，散列表的⼤⼩为10，在元素x插⼊散列表之前，已经6个元素插⼊到散列表中。x经过Hash算法之后，被散列到位置下标为7的位置，但是这个位置已经有数据了，所以就产⽣了冲突。于是我们就顺序地往后⼀个⼀个找，看有没有空闲的位置，遍历到尾部都没有找到空闲的位置，于是我们再从表头开始找，直到找到空闲位置2，于是将其插⼊到这个位置。

在散列表中查找元素的过程有点⼉类似插⼊过程。我们通过散列函数求出要查找元素的键值对应的散列值，然后⽐较数组中下标为散列值的元素和要查找的元素。如果相等，则说明就是我们要找的元素；否则就顺序往后依次查找。如果遍历到数组中的空闲位置，还没有找到，就说明要查找的元素并没有在散列表中。

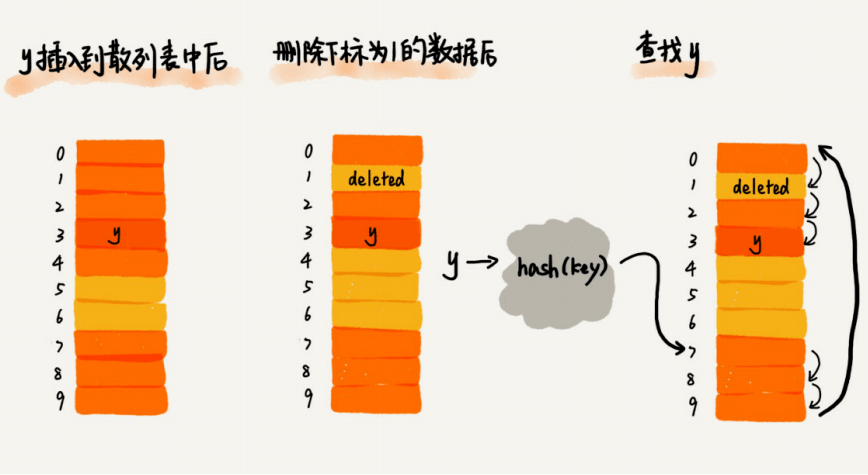
散列表跟数组⼀样，不仅⽀持插⼊、查找操作，还⽀持删除操作。对于使⽤线性探测法解决冲突的散列表，删除操作稍微有些特别。我们不能单纯地把要删除的元素设置为空。这是为什么呢？

在查找的时候，⼀旦我们通过线性探测⽅法，找到⼀个空闲位置，我们就可以认定散列表中不存在这个数据。但是，如果这个空闲位置是我们后来删除的，就会导致原来的查找算法失效。本来存在的数据，会被认定为不存在。这个问题如何解决呢？

我们可以将删除的元素，特殊标记为deleted。当线性探测查找的时候，遇到标记为deleted的空间，并不是停下来，⽽是继续往下探测。

你可能已经发现了，线性探测法其实存在很⼤问题。当散列表中插⼊的数据越来越多时，散列冲突发⽣的可能性就会越来越⼤，空闲位置会越来越少，线性探测的时间就会越来越久。极端情况下，我们可能需要探测整个散列表，所以最坏情况下的时间复杂度为O(n)。同理，在删除和查找时，也有可能会线性探测整张散列表，才能找到要查找或者删除的数据。

对于开放寻址冲突解决⽅法，除了线性探测⽅法之外，还有另外两种⽐较经典的探测⽅法，⼆次探测（Quadratic probing）和双重散列（Double hashing）。

所谓⼆次探测，跟线性探测很像，线性探测每次探测的步⻓是1，那它探测的下标序列就是hash(key)+0，hash(key)+1，hash(key)+2……⽽⼆次探测探测的步⻓就变成了原来的“⼆次⽅”，也就是说，它探测的下标序列就是hash(key)+0，hash(key)+12，hash(key)+22……

所谓双重散列，意思就是不仅要使⽤⼀个散列函数。我们使⽤⼀组散列函数hash1(key)，hash2(key)，hash3(key)……我们先⽤第⼀个散列函数，如果计算得到的存储位置已经被占⽤，再⽤第⼆个散列函数，依次类推，直到找到空闲的存储位置。

链表法

链表法是⼀种更加常⽤的散列冲突解决办法，相⽐开放寻址法，它要简单很多。我们来看这个图，在散列表中，每个“桶（bucket）”或者“槽（slot）”会对应⼀条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中。

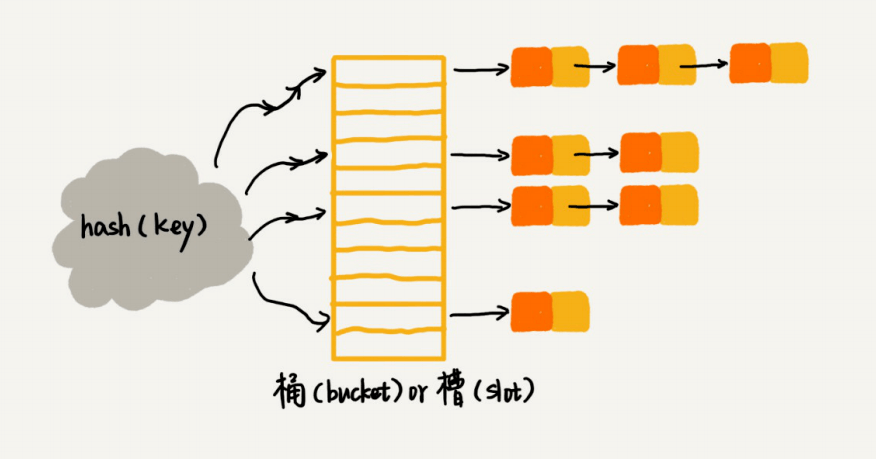
当插⼊的时候，我们只需要通过散列函数计算出对应的散列槽位，将其插⼊到对应链表中即可，所以插⼊的时间复杂度是O(1)。当查找、删除⼀个元素时，我们同样通过散列函数计算出对应的槽，然后遍历链表查找或者删除。那查找或删除操作的时间复杂度是多少呢？

实际上，这两个操作的时间复杂度跟链表的⻓度k成正⽐，也就是O(k)。对于散列⽐较均匀的散列函数来说，理论上讲，k=n/m，其中n表示散列中数据的个数，m表示散列表中“槽”的个数。

本作品采用《CC 协议》，转载必须注明作者和本文链接