条件概率、全概率、贝叶斯公式理解
条件概率公式
\displaystyle P(AB)=P(A)P(B|A)=P(B)P(A|B)
即事件A和事件B同时发生的概率等于在发生A的条件下B发生的概率乘以A的概率。有条件概率公式推出贝叶斯公式:
\displaystyle P(B|A)=\frac{P(A|B)P(B)}{P(A)}
即已知P(A|B)、P(A)、P(B)可以计算出P(B|A)。
假设B是由相互独立的事件组成的概率空间
\left\{B_1,B_2,\cdots B_n\right\}
则P(A)可以用全概率公式展开:
P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+\cdots P(A|B_n)P(B_n)
贝叶斯公式表示成:
\displaystyle P(B_i|A)=\frac{P(A|B_i)P(B_i)}{P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+\cdots P(A|B_n)P(B_n)}
常常把P(B_i|A)称做后验概率,而P(A|B_n)P(B_n)为先验概率,而P(B_1)又叫做基础概率。
贝叶斯公式:
\displaystyle P(B_i|A)=\frac{P(Bi)P(A|B_i)}{\sum\limits_{i=1}^nP(B_i)P(A|B_i)}
贝叶斯法则的原理
通常,事件A在事件B发生的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
作为一个规范的原理,贝叶斯法则对于所有概率的解释是有效的;然而,频率主义者和贝叶斯主义者对于在应用中概率如何被赋值有着不通的看法:频率主义者根据随机事件发生的频率,或总体样本里面的个数来赋值概率;贝叶斯主义者要根据未知的命题来赋值概率。一个结果就是,贝叶斯主义者有更多的机会使用贝叶斯法则。
贝叶斯法则是关于随机事件A和B的条件概率和边缘概率的/
\displaystyle P(A|B)=\frac{P(B|A)P(A)}{P(B)}\propto L(A|B)P(A)
其中L(A|B)是在B发生的情况下A发生的可能性。
在贝叶斯法则中,每个名次都有约定俗成的名称:
- P(A) 是 A 的先验概率或边缘概率。之所以称为”先验”是因为它不考虑任何 B 方面的因素。
- P(A|B) 是已知 B 发生后 A 的条件概率,也由于得自 B 的取值而被称作 A 的后验概率。
- P(B|A) 是已知 A 发生后 B 的条件概率,也由于得自 A 的取值而被称做 B 的后验概率。
- P(B) 是 B 的先验概率或边缘概率,也称作标准化常量。
贝叶斯法则可表述为:
后验概率 = (似然度 * 先验概率) / 标准化常量。
也就是说,后验概率与先验概率和似然度的乘积成正比。
另外,比例\frac{P(B|A)}{P(B)}也有时被称做标准似然度,贝叶斯法则可表述为:
后验概率 = 标准似然度 * 先验概率
要理解贝叶斯推断,必须先理解贝叶斯定力。后者实际上就是计算”条件概率”的公式。
所谓”条件概率”,就是至在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
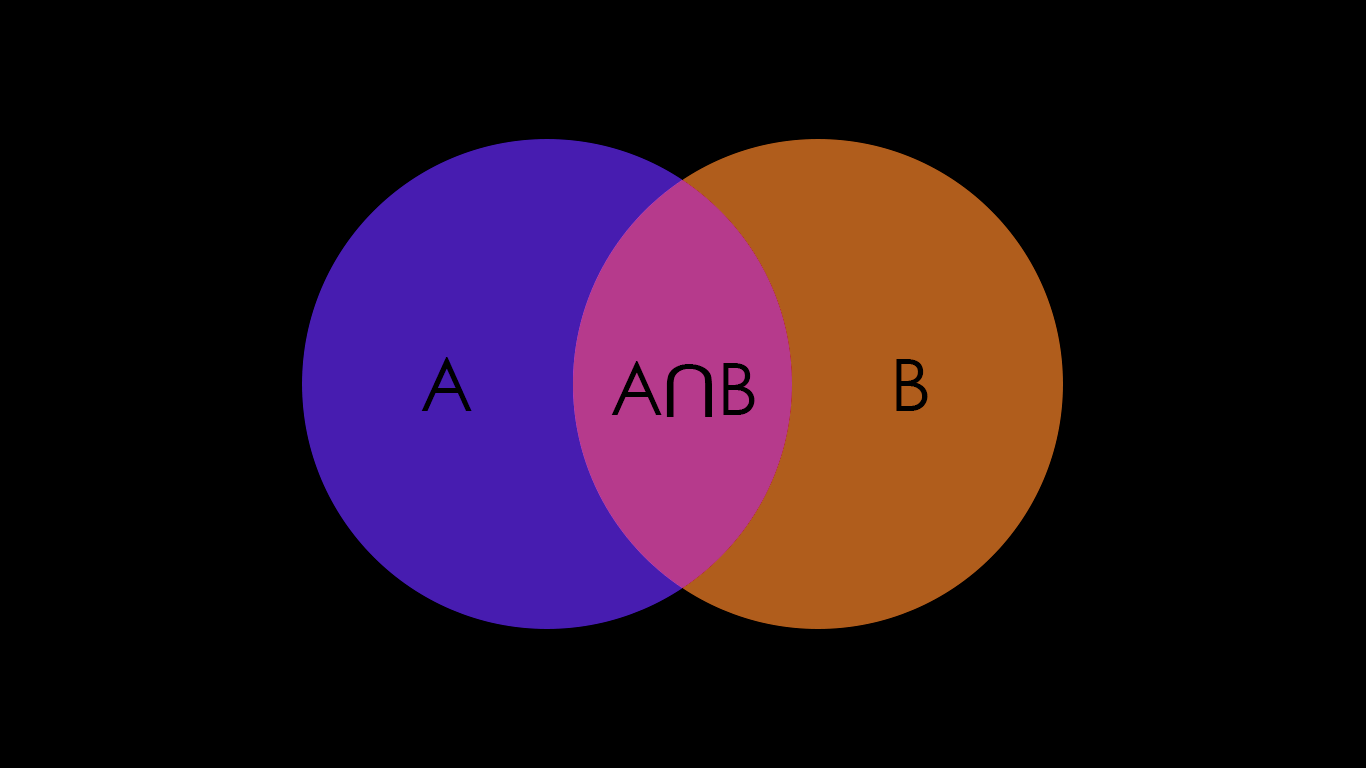
\displaystyle P(A|B)=\frac{P(A\bigcap B)}{P(B)}\\{}\\ \Rightarrow P(A\bigcap B)=P(A|B)P(B)\\{}\\ \Rightarrow P(A\bigcap B)=P(B|A)P(A)\\{}\\ \Rightarrow P(A|B)P(B)=P(B|A)P(A)\\{}\\ \Rightarrow P(A|B)=\frac{P(B|A)P(A)}{P(B)}
本作品采用《CC 协议》,转载必须注明作者和本文链接




 关于 LearnKu
关于 LearnKu



