全概率公式理解

全概率公式

样本空间S是两个事件A与A^{\prime}的和。

加入事件B，事件B被划分成两个部分。

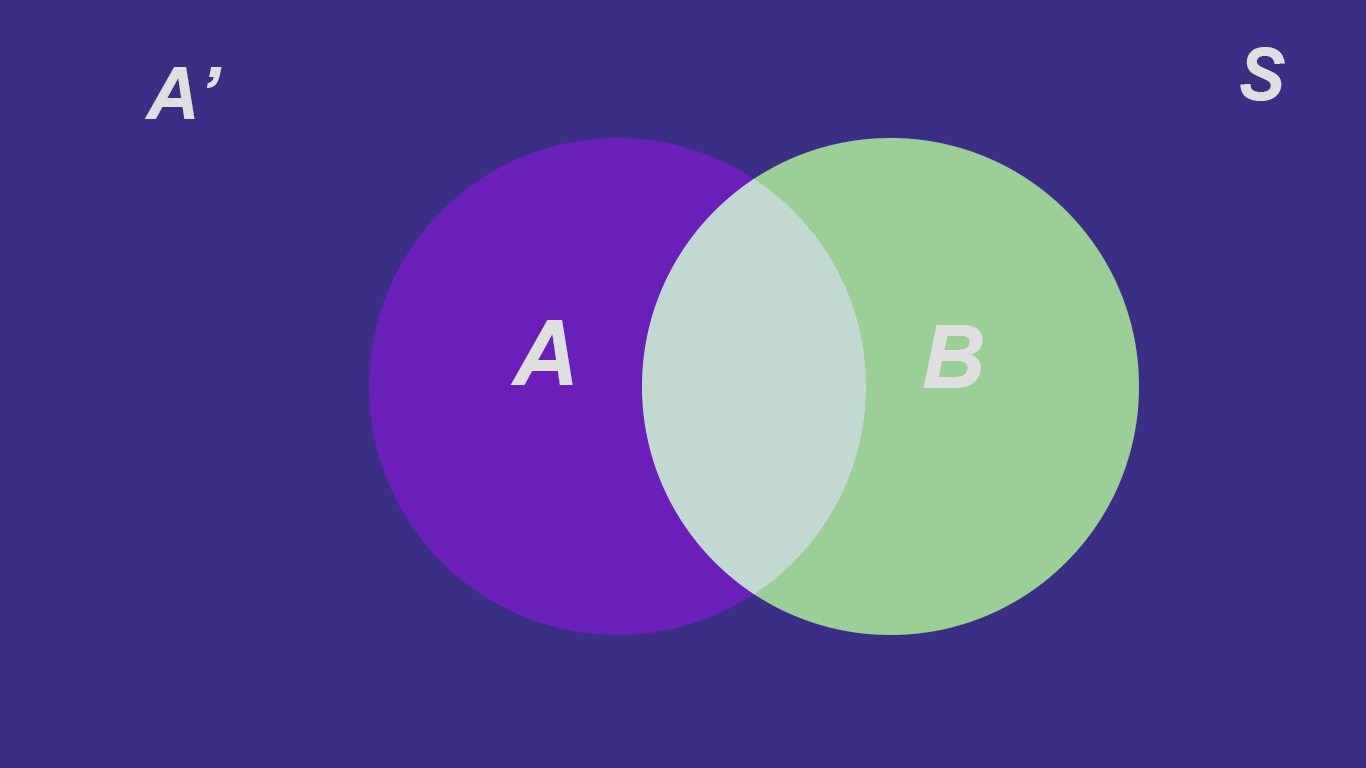
即

\displaystyle P(B)=P(B\bigcap A)+P(B\bigcap A^\prime)\\{}\\ P(B\bigcap A)=P(B|A)P(A)\\{}\\ \Rightarrow P(B)=P(B|A)P(A)+P(B|A^\prime)P(A^\prime)

这就是全概率公式，含义是：如果A和A\prime构成样本空间的一个划分，那么事件B的概率就等于A和A\prime的概率分别乘以B对这两个事件的条件概率只和。
所以条件概率的另一种写法：

\displaystyle P(A|B)=\frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|A^\prime)P(A^\prime)}

贝叶斯推断的含义

\displaystyle P(A|B)=P(A)\frac{P(B|A)}{P(B)}

P(A) 为”先验概率”，即在 B 事件发生之前，对 A 事件概率的一个判断。P(A|B) 称为”后验概率”，即在 B 事件发生之后，对 A 事件概率的重新评估。P(B|A)/P(B) 称为”可能性函数”，这是一个调整因子，使得预估概率更接近真实概率。
所以条件概率可以理解成：

后验概率 = 先验概率 x 调整因子

这就是贝叶斯推断的含义。我们先预估一个”先验概率”，然后加入实验结果，看这个实验到底是增强还是削弱了”先验概率”，由此得到更接近事实的”后验概率”。

在这里，如果”可能性函数” P(B|A)/P(B)>1，意味着”先验概率”被增强，事件 A 的发生的可能性变大；如果”可能性函数”=1，意味着 B 事件无助于判断事件 A 的可能性；如果”可能性函数”<1，意味着”先验概率”被削弱，事件A的可能性变小。

本作品采用《CC 协议》，转载必须注明作者和本文链接