计算机组成与体系结构-数据的表示-码制
0 / 0 / 创建于 4年前
wangchunbo 的个人博客
码制
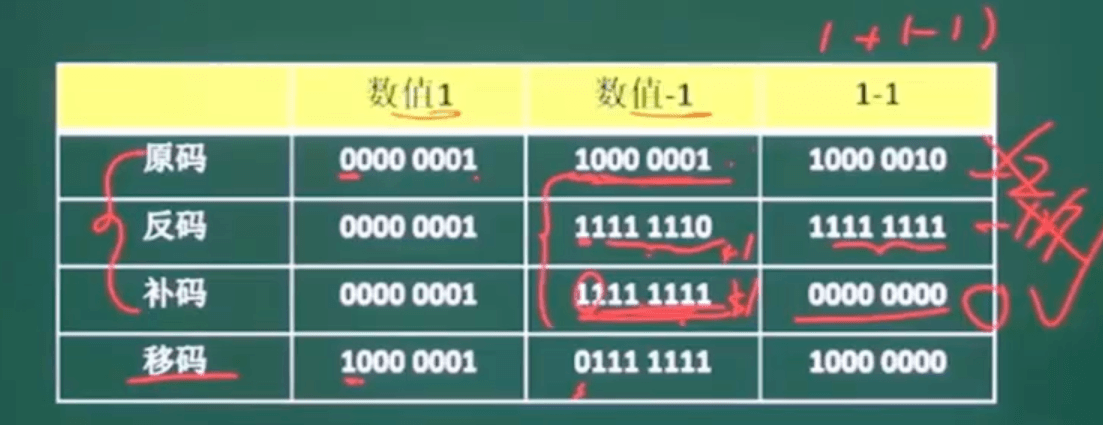
在计算机中，数据编码方式可以有多种，最为常见的有原码、反码、补码、移码。一个正数的 原码、补码、反码是相同的，负数则不同。
原码
二进制
一般8位，
将最高位用做符号位（0表示正数，1表示负数），其余各位代表数值本身的绝对值的表示形
式。这种方式是最容易理解的。
例如 +1的原码是00000001，–1的原码是10000001。
因为是8位数。 首位为正负。 所以 1 表示为 2^0 前面的则只能全是0 了。
所以 1 然后补齐 0000000 得到 00000001。
原码的计算不准确问题
但是直接使用原码在计算时却会有麻烦，比如(1)10+(–1)10=0，如果直接使用原码则：
(00000001)2＋(10000001)2=(10000010)2
解释： 直接相加 然后 逢2 进1 则 10000002 因为有2 所以变为10000010
这里 （）N 表示是 N进制
这样计算的结果是–2，也就是说，使用原码直接参与计算可能会出现错误的结果。所以，原码
的符号位不能直接参与计算，必须和其它位分开，这样会增加硬件的开销和复杂性
反码
正数的反码与原码相同。负数的反码符号位为1，其余各位为该数绝对值的原码按位取反。这个
取反的过程使得这种编码称为“反码”。
例如，–1的反码：11111110。
同样对上面的加法，使用反码的结果是：
(00000001)2+(11111110)2=(11111111)2
这样的结果是负0，而在人们普遍的观念中，0是不分正负的。反码的符号位可以直接参与计
算，而且减法也可以转换为加法计算
补码
正数的补码与原码相同。负数的补码是该数的反码加1，这个加1就是“补”。
例如，–1的补码：11111110+1=11111111。
再次做加法是这样的：
(00000001)2+(11111111)2=(00000000)2
直接使用补码进行计算的结果是正确的。
对一个补码表示的数，要计算其原码，只要对它再次求补，可得该数的原码。
由于补码能使符号位与有效值部分一起参加运算，从而简化运算规则，同时它也使减法运算转
换为加法运算，进一步简化计算机中运算器的电路，这使得在大部分计算机系统中，数据都使用补
码表示。
移码
移码是对补码的符号位取反得到的一种编码。移码只用于表示浮点数的阶码，所以只用于整
数。
例如，-1的移码为：01111111。
看大图
本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号