先上一副各个排序算法的比较图（重点）

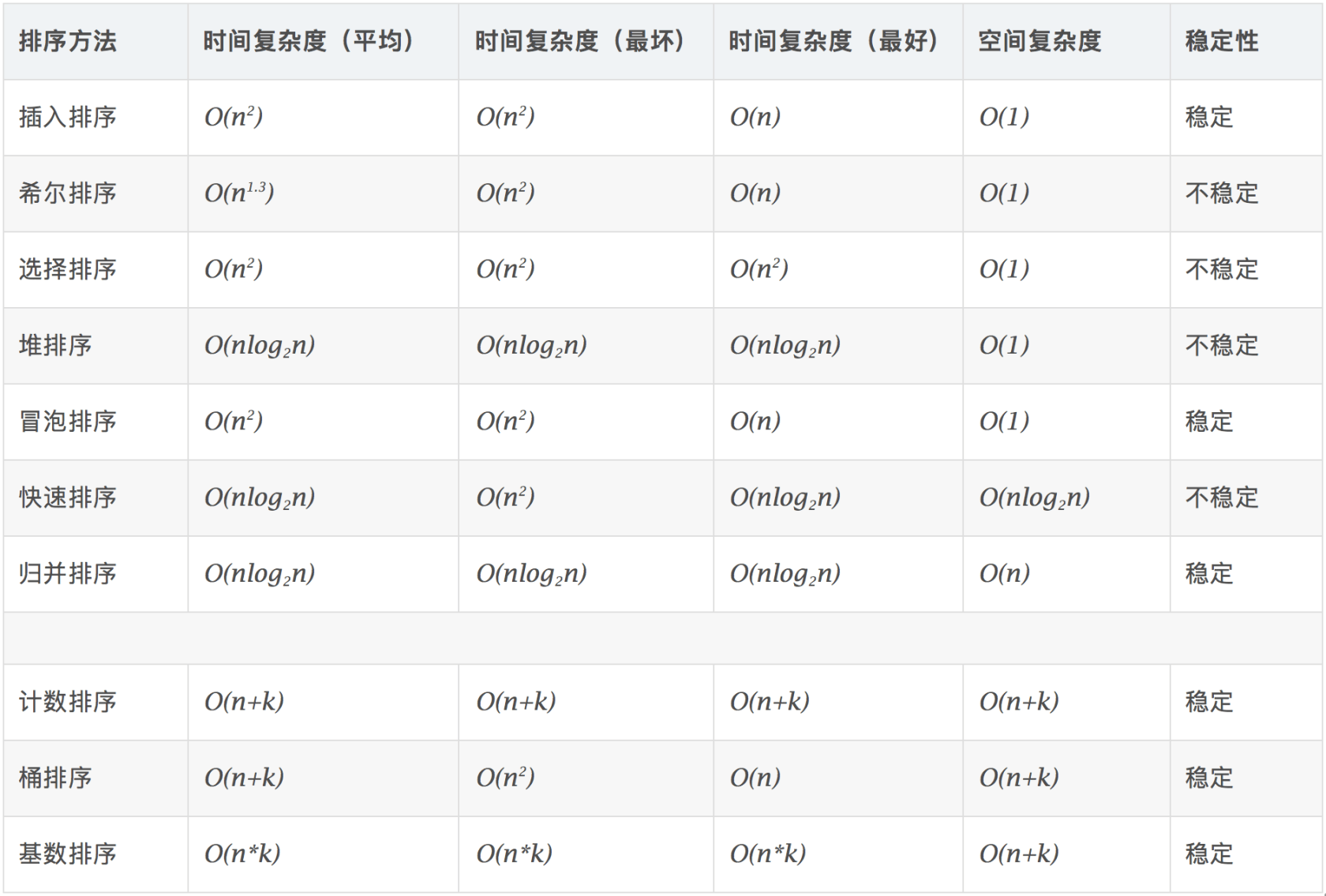
1. 冒泡排序

思想：冒泡排序是一种简单的排序，它不断的从头开始访问整个序列，如果当前的元素比下一个大，就交换，这样在每一趟遍历都能把当前未排序的序列中最大的元素找到并放到最后！（这个算法的名字由来是因为大的元素会经由交换慢慢“浮”到数列的底端。）

    for (int i = 0; i < len -1; i++) { //遍历的次数，len-1即可，最后一遍第一个元素无需在进行
            for(int j = 0;j<len - 1 - i;j++){ 
            //注意要减去i哦，毕竟每一次遍历都能让最后的i+1个数有序！
                if(arr[j] > arr[j+1]){
                    temp = arr[j+1];
                    arr[j+1] = arr[j];
                    arr[j] = temp;
                }
            }
            System.out.println("第"+(i+1)+"趟排序后:"+Arrays.toString(arr) );
        }

冒泡排序算法改进！
通过加上一个标志位，判断自此遍历有无交换，若无交换，则说明当前序列俨然有序！无需再进行遍历！这样会导致最好情况下时间复杂度为O(n)!

# 
        boolean flag = false; //是否交换
        for (int i = 0; i < len - 1; i++) { 
        //遍历的次数，len-1即可，最后一遍第一个元素无需进行
            flag = false;
            for (int j = 0; j < len - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = temp;
                    flag = true;
                }
            }
            if (!flag) {
                break;
            }
        }

2.选择排序

首先，找到数组中最小的那个元素的下标，其次，将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。其次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。

        int minIndex = 0;
        int temp;
        for (int i = 0; i < len - 1; i++) { //遍历的次数，len-1即可，最后一个元素无需在进行
            minIndex = i;
            for (int j = i ; j < len; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j; // 不断更新下标导致了该算法的不稳定性
                }
            }
            if(minIndex != i){ //判断一下，是否等于自身，等于自身说明自身是最小，而无需交换
                temp = arr[i];
                arr[i] = arr[minIndex];
                arr[minIndex] = temp;
            }
        }

3.插入排序

插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

        for (int i = 1; i < len; i++) { //从1开始是认定第一个元素已经有序
            int cur = arr[i]; //当前要插入的元素
            int  pos = i - 1; //有序序列的最后一个元素下标
            while (pos >= 0 && arr[pos] > cur ){
                arr[pos + 1] = arr[pos];
                pos--;
            }
            arr[pos + 1] = cur;
        }

4.归并排序

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。
过程如下图所示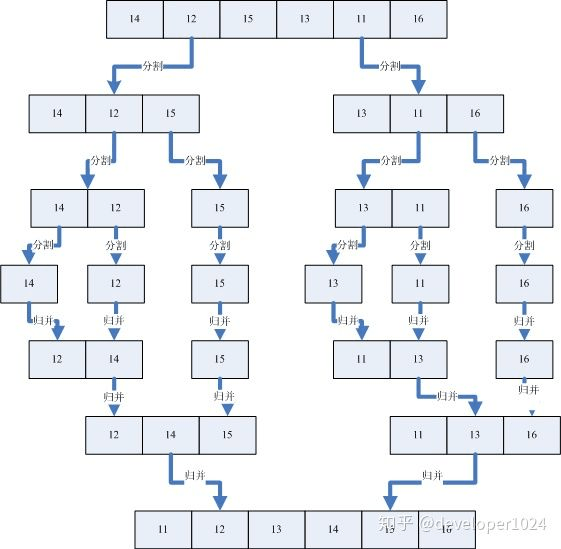

话不多说上代码！

    public static void mergesort(int[] arr, int L, int R) {
        if (L >= R) {
            return;
        }
        int mid = L + ((R - L) >> 1); //分治，分成两部分！
        mergesort(arr, L, mid);//左半部分继续递归分治
        mergesort(arr, mid + 1, R);//右半部分继续递归分治
        merge(arr, L, R, mid);//合并！！！
    }

    public static void merge(int[] arr, int l, int r, int mid) {
        int i = l;
        int j = mid + 1;
        int[] res = new int[r - l + 1]; //额外数组空间
        int index = 0;
        while (i <= mid && j <= r) {
            if (arr[i] > arr[j]) {
                res[index++] = arr[j++];
            } else {
                res[index++] = arr[i++];
            }
        }
        while (i <= mid) {
            res[index++] = arr[i++];
        }
        while (j <= r) {
            res[index++] = arr[j++];
        }
        for (int k = l; k <= r; k++) {
            arr[k] = res[k - l];
        }
    }

关于归并排序的空间复杂度分析
归并排序每次递归需要用到一个辅助表，长度与待排序的表相等，虽然递归次数是O(log2n)，但每次递归都会释放掉所占的辅助空间，所以下次递归的栈空间和辅助空间与这部分释放的空间就不相关了，因而空间复杂度还是O（n）。

5.堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
　堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

public void heapSort(int[] arr) {
        //建堆！
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            //从第一个非叶子节点从下到上，从右到左建堆！
            adjustHeap(arr, i, arr.length);
        }
        //将第一个与最后一个交换，再调整堆
        for (int i = arr.length - 1; i > 0; i--) {
            swap(arr, 0, i);
            adjustHeap(arr, 0, i);
        }
    }

    public void adjustHeap(int[] arr, int i, int len) {
        int temp = arr[i];
        for (int j = 2 * i + 1; j < len; j = 2 * j + 1) {
            if (j + 1 < len && arr[j] < arr[j + 1]) {
                //如果左节点小于右节点，则定位于右节点
                j++;
            }
            if (temp < arr[j]) {
                arr[i] = arr[j];
                i = j;
            }else{
                break;
            }
        }
        arr[i] = temp;
    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ temp;
        arr[j] = arr[j] ^ temp;
    }

6.快排

话不多说上代码!!

public void sort(int[] arr, int L, int R) {
        if (L < R) {
            int[] res = partition(arr, L, R);
            sort(arr, 0, res[0] - 1);
            sort(arr, res[1] + 1, R);
        }
    }

    public int[] partition(int[] arr, int L, int R) { //partition过程！
        if (L == R) {
            return new int[]{L, L};
        }
        int left = L - 1;
        int right = R;
        int cur = L;
        while (cur < right) {
            if (arr[cur] < arr[R]) {
                swap(arr, cur++, ++left);
            } else if (arr[cur] > arr[R]) {
                swap(arr, cur, --right);
            } else {
                cur++;
            }
        }
        swap(arr, cur, R);
        return new int[]{left + 1, cur};
    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
    }

本作品采用《CC 协议》，转载必须注明作者和本文链接